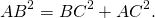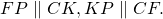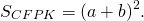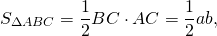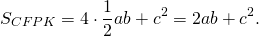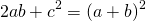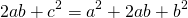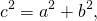в каком треугольнике квадрат гипотенузы равен сумме квадратов катетов

Теорема Пифагора

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

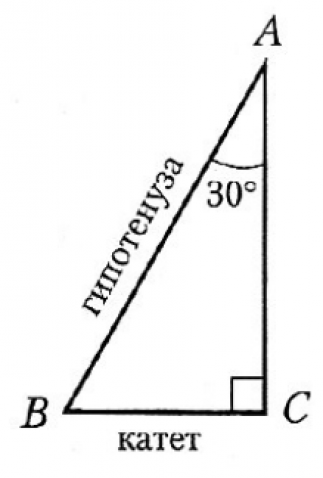
Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Пошаговое доказательство:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?

значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

Ответ: треугольник не является прямоугольным.

Источник

Теорема Пифагора

Теорема Пифагора в геометрии важна не меньше, чем таблица умножения в арифметике. Решение многих геометрических задач (как в планиметрии, так и в стереометрии), сводится к рассмотрению прямоугольных треугольников и применению этой замечательной теоремы.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Существует множество разнообразных способов доказательства теоремы Пифагора. Ограничимся лишь одним из них.

Дано : ∆ ABC, ∠C=90º.

На гипотенузе AB построим квадрат со стороной c.

На продолжении стороны AC отложим отрезок AF, AF=a,

на продолжении стороны BC — отрезок BK, BK=b.

CF=AF+AC=a+b, CK=BC+BK=a+b, то есть CF=CK=a+b.

Через точки F и K проведём прямые, параллельные катетам:

Четырёхугольник CFPK — параллелограмм (по определению).

А так как ∠C=90º и CF=CK, то CFPK — квадрат со стороной a+b.

Так как площадь квадрата равна квадрату его стороны, то

С другой стороны, площадь CFPK равна сумме площадей четырёх прямоугольных треугольников с катетами b и c и квадрата со стороной c.

Площадь прямоугольного треугольника равны половине произведения его катетов:

площадь квадрата со стороной c равна c².

Приравняем правые части формул площади CFPK:

После упрощения получаем

Источник

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

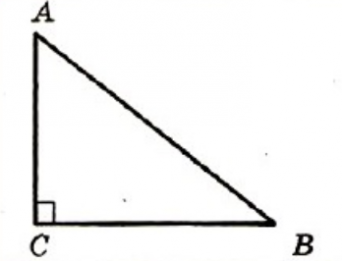
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

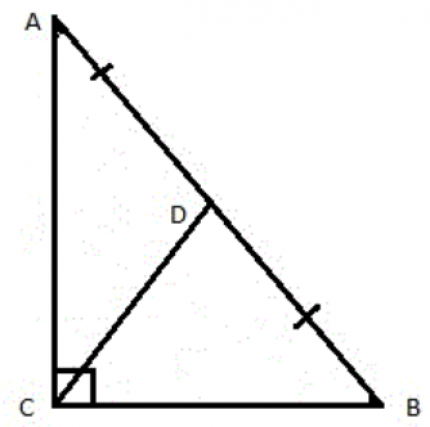
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

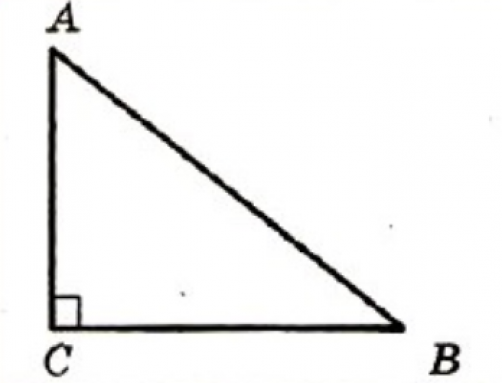
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Источник

Теорема Пифагора онлайн

С помощю этого онлайн калькулятора можно найти неизвестную сторону прямоугольного треугольника используя теорему Пифагора. Теоретическую часть и численные примеры смотрите ниже.

Теорема Пифагора. Доказательство

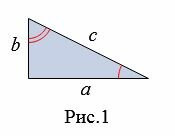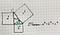
Доказательство (метод площадей). Пусть задан прямоугольный треугольник с катетами a и b и гипотенузой c (Рис.1). Докажем, что \( \small c^2=a^2+b^2. \)

Построим квадрат со стороной a+b из четырех таких прямоугольных треугольников (Рис.2). Тогда внутренний белый четырехугольник будет квадратом со стороной c.

Действительно. В прямоугольных треугольниках (Рис.2) \( \small \angle 1 +\angle 2=90° \) Следовательно, каждый угол квадрата со стороной c равен \( \small \angle 3=180&deg-(\angle 1 +\angle 2)=180°-90°=90°.\)

Далее, площадь квадрата со стороной a+b равна:

Площадь квадрата со стороной c равна:

Площадь каждого прямоугольного треугольника на рисунке 2 равна:

Площадь квадрата со стороной a+b равна сумме площади квадрата со стороной c и четырех площадей прямоугольных треугольников c катетами a и b:

Подставляя (1)-(3) в (4), получим:

\( \small a^2+b^2=с^2. \)

Сложив уравнения (5) и (6), получим

Доказательство (Евклид). Пусть задан прямоугольный треугольник ABC с катетами a, b и гипотенузой c (Рис.4). Докажем, что \( \small c^2=a^2+b^2. \)

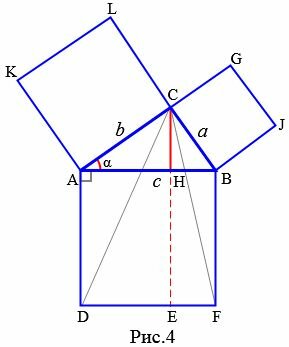Достаточно доказать, что площадь квадрата ABFD равна сумме площадей ACLK и BCGJ:

Площадь треугольника ACD по двум сторонам и углу между ними равен:

Учитывая, что \( \small \sin \angle ACH=\sin (90°-\alpha)=\sin \alpha, \) применим теорему синусов для прямоугольного треугольника ACH:

Подставляя (8) в (7), получим:

Применим теорему синусов для прямоугольного треугольника ABC:

Подставляя (10) в (7), получим:

Учитывая, что \( \small AD=AB, \) получим:

Аналогично можно показать, что

Сложив (13) и (14), получим:

Теорема Пифагора. Примеры и решения

Решение: Для нахождения гипотенузы воспользуемся формулой Пифагора:

Подставляя значения \( \small a \) и \( \small b \) в (15), получим:

Ответ:

Решение: Для нахождения неизвестного катета воспользуемся теоремой Пифагора:

Подставляя значения \( \small a \) и \( \small b \) в (16), получим:

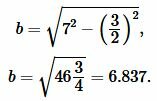Ответ:

Источник

Оригинальное доказательство теоремы Пифагора

Знаменитую теорему Пифагора — «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» — знают все со школьной скамьи.

Ну, вы помните «Пифагоровы штаны», которые «во все стороны равны» — схематический рисунок, поясняющий теорему греческого ученого.

Здесь a и b — катеты, а с — гипотенуза:

Сейчас я вам расскажу об одном оригинальном доказательстве этой теоремы, о котором вы, возможно, не знали…

Но, сначала рассмотрим одну лемму — доказанное утверждение, которое полезно не само по себе, а для доказательства других утверждений (теорем).

Возьмем прямоугольный треугольник с вершинами X, Y и Z, где Z — прямой угол и опустим перпендикуляр с прямого угла Z на гипотенузу. Здесь W — точка, в которой высота пересекается с гипотенузой.

Эта линия (перпендикуляр) ZW разбивает треугольник на подобные копии самого себя.

Напомню, что подобными называются треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

В нашем примере образовавшиеся треугольники XWZ и YWZ подобны друг другу и также подобны исходному треугольнику XYZ.

Доказать это несложно.

Начнем с треугольника XWZ, обратите внимание, что ∠XWZ = 90, и поэтому ∠XZW = 180–90-∠X. Но 180–90-∠X — это именно то, что ∠Y, поэтому треугольник XWZ должен быть подобным (все углы равны) треугольнику XYZ. Такое же упражнение можно выполнить для треугольника YWZ.

Лемма доказана! В прямоугольном треугольнике высота (перпендикуляр), опущенная на гипотенузу, разбивает треугольник на два подобных, которые в свою очередь подобны исходному треугольнику.

Но, вернемся к нашим «Пифагоровым штанам»…

Опустим перпендикуляр на гипотенузу c. В результате у нас образовались два прямогульных треугольника внутри нашего прямоугольного треугольника. Обозначим эти треугольники (на картинке вверху зеленым цветом) буквами A и B, а исходный треугольник — буквой С.

Разумеется, площадь треугольника С равна сумме площадей треугольников A и B.

Теперь разобьем фигуру вверху («Пифагоровы штаны») на три фигурки-домика:

Как мы уже знаем из леммы, треугольники A, B и C подобны друг другу, поэтому и образовавшиеся фигурки-домики также подобны и являются масштабированными версиями друг друга.

Это означает, что соотношение площадей A и a², — это то же самое, что отношение площадей B и b², а также C и c².

Обозначим это соотношение площадей треугольника и квадрата в фигуре-домике буквой k.

Т.е. k — это некий коэффициент, связывающий площадь треугольника (крыши домика) с площадью квадрата под ним:
k = A / a² = B / b² = C / c²

Из этого следует, что площади треугольников можно выразить через площади квадратов под ними таким образом:
A = ka², B = kb², и C = kc²

Но, мы помним, что A+B = C, а значит, ka² + kb² = kc²

А это и есть доказательство теоремы Пифагора!

По материалам заметки Колина Фразера ( Colin Fraser)

Источник