в каком треугольнике высота делит сторону пополам

Свойства высоты равностороннего треугольника

В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.

Примечание: треугольник называется равносторонним, если все его стороны равны.

Свойства высоты в равностороннем треугольнике

Свойство 1

Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

Свойство 2

Все три высоты в равностороннем треугольнике имеют одинаковую длину.

Свойство 3

Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.

Свойство 4

Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.

Свойство 5

Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.

Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.

Свойство 6

Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:

a – сторона треугольника.

Пример задачи

Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.

Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.

Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):

Источник

Треугольник. Важные факты о высоте, биссектрисе и медиане

Определения

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

Доказательство

Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.

Теорема

Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).

Доказательство

Теорема

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

Доказательство

Теорема

Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.

Доказательство

Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac>> = \dfrac = \dfrac\]

Теорема

Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

Доказательство

Источник

Равнобедренный треугольник: свойства, признаки и формулы

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

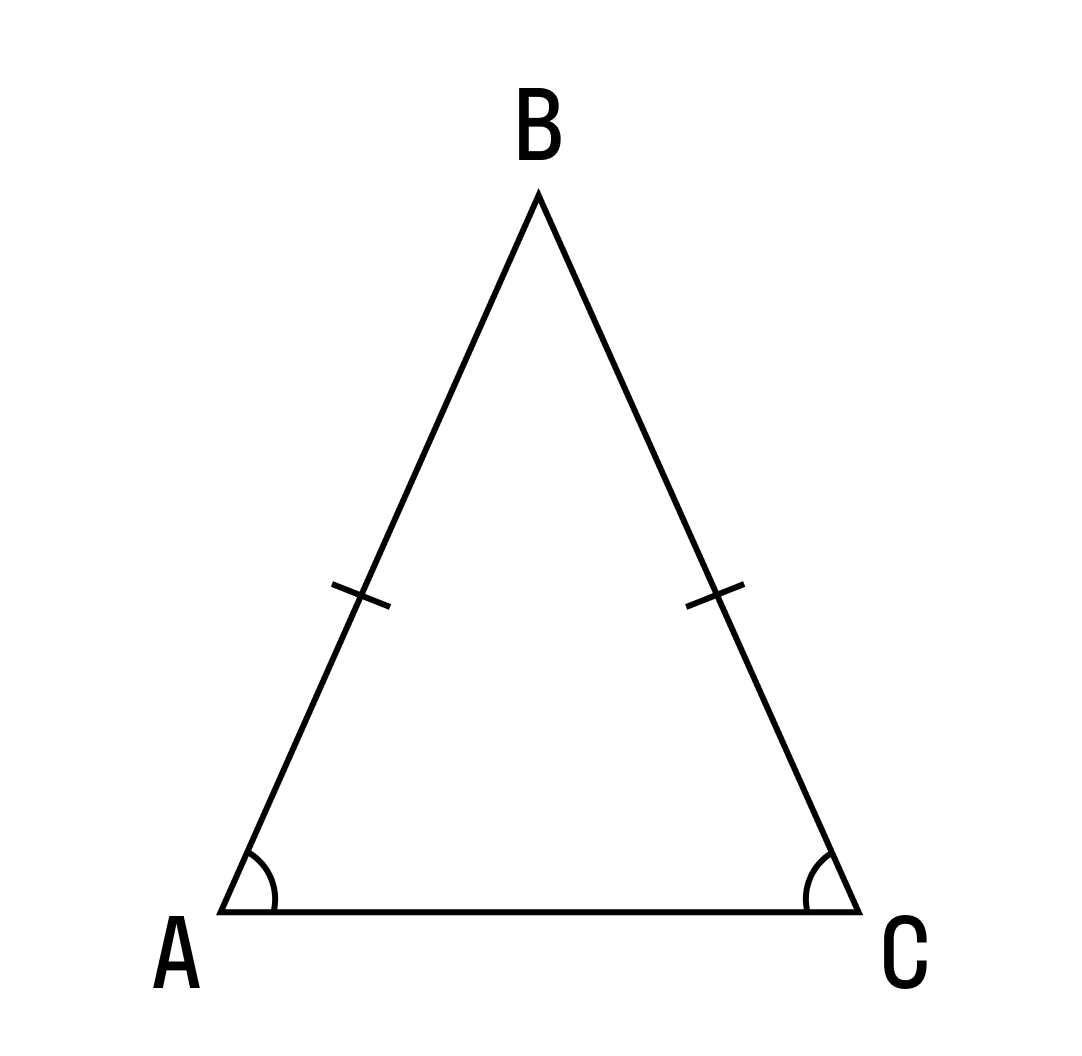
Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.

Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.

А вот и доказательство:

Вуаля, сразу три теоремы доказаны.

Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).

Дано два Δ ABC = Δ A1B1C1.

Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.

Если все стороны совпадают — треугольники равны, а теорема доказана.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

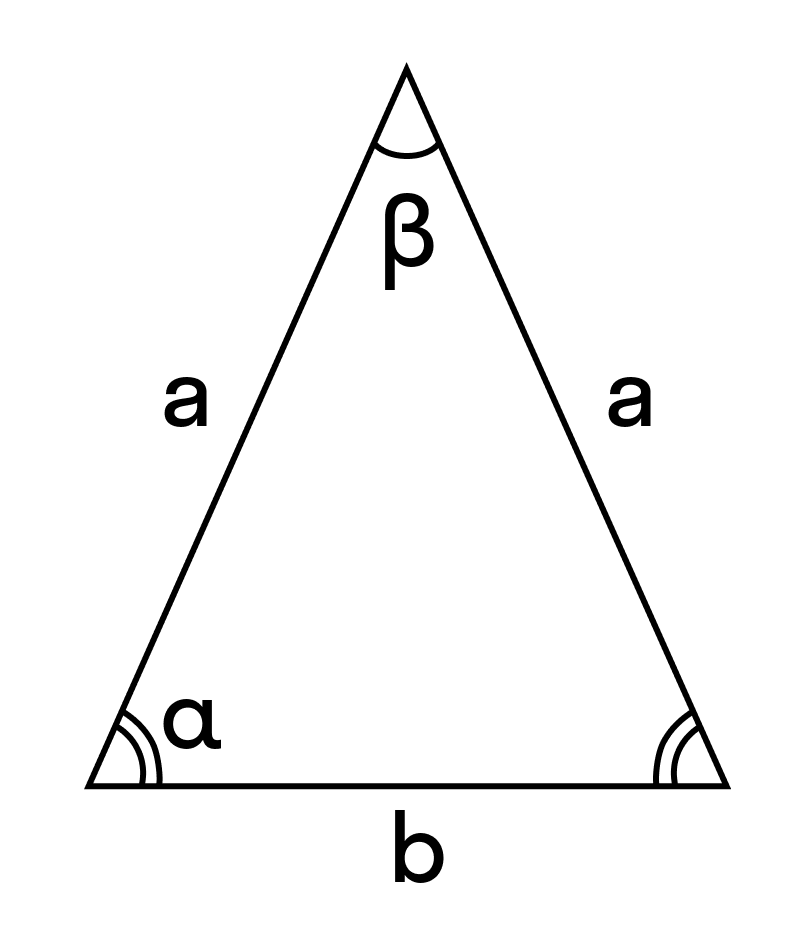
Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

Формулы длины равных сторон равнобедренного треугольника (стороны a):

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘

Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.

Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘

Источник

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC. Следовательно, ∠BAD = ∠ACD.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

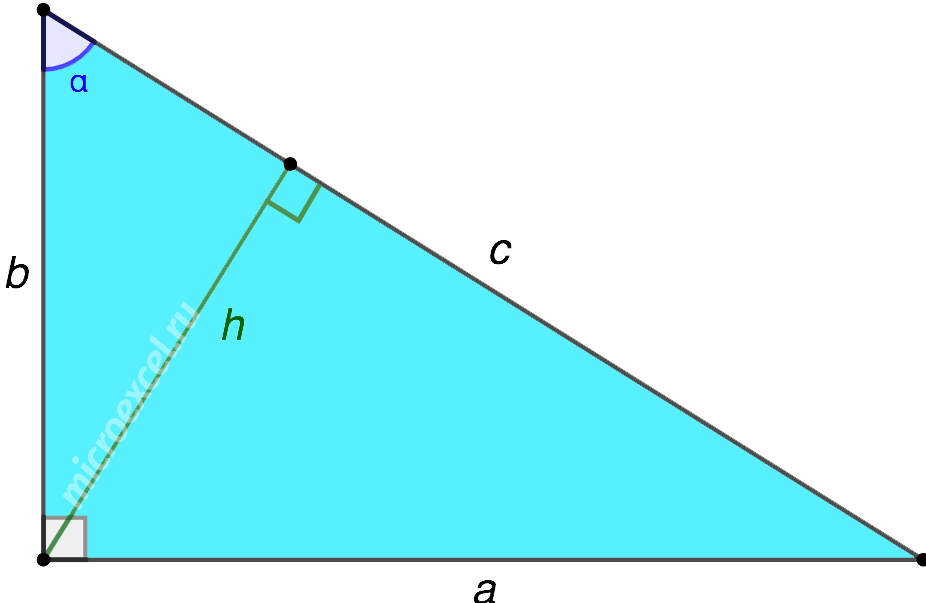
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

Источник

В каком треугольнике высота делит сторону пополам

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

Свойства серединных перпендикуляров треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Источник