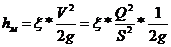в какую энергию превращается энергия потерянная потоком в местном сопротивлении

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Содержание статьи

Коэффициент гидравлического сопротивления

Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:

где ρ — плотность среды, g — ускорение свободного падения.

В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.

где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

Значение коэффициента ξ_{вн. суж} от значения отношения (F₂/F₁)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле

ξ _{поворот} = 0,946sin(α/2) + 2.047sin(α/2) 2

где α – угол поворота трубопровода.

Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:

ξ_вх = 0,505 + 0,303sin α + 0,223 sin α 2

Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

Гидравлическое сопротивление полностью открытой запорной арматуры равно

ξ_{вентиля} = от 2,9 до 4,5

Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.

Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.

Для диафрагмы с острыми краями:

Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

Видео о гидравлическом сопротивлении

На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)

Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.

Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

Источник

Шпоры / Местные сопротивления

Потери напора в местных сопротивлениях пропорциональны…

Коэффициент местного сопротивления зависит от числа Рейнольдса только при…

… малых скоростях движения и малых размерах проходного сечения.

Две одинаковые диафрагмы установлены в трубе. Укажите, в каком случае потери напора на двух диафрагмах равны потери напора на одной диафрагме.

Когда расстояние между диафрагмами равно нулю.

Для какого из перечисленных местных сопротивлений потери напора установлены аналитическим путём?

Как изменятся потери напора, если местное сопротивление переставить из начала трубы в её конец?

В какой зоне потока физически реализуются потери напора в местном сопротивлении?

В зонах деформации потока.

От чего зависит длина влияния местного сопротивления, установленного на трубопроводе?

а) от шероховатости стенок трубопровода;

б) от диаметра трубопровода;

в) от местного сопротивления;

г) от коэффициента гидравлического сопротивления трубопровода.

Укажите, что является длиной влияния местного сопротивления, установленного в трубопроводе:

а) участок трубопровода, на котором эпюра скорости становится такой же, как перед местным сопротивлением;

б) участок трубопровода, на котором поток трансформируется в равномерный.

Как определяются общие потери нескольких местных сопротивлений, установленных на трубопроводе с малым расстоянием друг от друга?

Складываются с учётом степени взаимного влияния.

Как определяются общие потери нескольких местных сопротивлений, установленных на трубопроводе с большим расстоянием друг от друга?

Что такое эквивалентная длина местного сопротивления?

Длина участка трубопровода, в пределах которой потери напора на трение равны потерям в местном сопротивлении.

В какую энергию превращается энергия, потерянная потоком в местном сопротивлении?

От чего зависит коэффициент местного сопротивления вентиля при данной его конструкции?

а) от степени открытия;

б) шероховатость трубы;

Укажите фактор, влияющий на коэффициент местного сопротивления при повороте трубы:

Коэффициент гидравлического сопротивления.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Как определяются общие потери нескольких местных сопротивлений установленных на трубопроводе с малым расстоянием друг от друга?

2.СКЛАДЫВАЮТСЯ С УЧЕТОМ СТЕПЕНИ ВЗАИМНОГО ВЛИЯНИЯ

Как определяются общие потери нескольких местных сопротивлений установленных на трубопроводе с большим расстоянием друг от друга?

4.Длина участка трубопровода в пределах которой потери напора на трение равны потерям в местном сопротивлении

В какую энергию превращается энергия потерянная поток в местном сопротивлении?

От чего зависит коэффицетн местного сопротивления вентиля при данной его конструкции?

3.от степени покрытия

4.КОЭФФИЦЕНТ ГИДРАВЛИЧЕСКОГО СОПРОТИВЛЕНИЯ

3. на основании малой величины трения о стенки трубы возникающей в зоне возвратного движения жидкости

Укажите в какой вид энергии превращается потерянная потоком энергия при расширении трубопровода

3.В ТЕПЛОВУЮ ЭНЕРГИЮ

Укажите на каком основании гидростатическое распределение давления по высоте поперечного сечения трубопровода не учитывается при определение гидравлических потерь во внезапно расширяющеемся трубопроводе?

2.ГИДРОСТАТИЧЕСКОЕ ИЗМЕНЕНИЕ ДАВЛЕНИЯ НЕЗНАЧИТЕЛЬНО ПО СРАВНЕНИЮ С ИЗБЫТОЧНЫМ ДАВЛЕНИЕМ

Истечение жидкости из насадков и коротких труб

Укажите физическую особенность течения через насадок?

2. отсутствует сжатие струи на выходе из насадка

Укажите физическую особенность течения через насадок?

1. происходит сжатие струи в насадке

Укажите физическую особенность течения через насадок?

3. возникает трение струи о стенки насадка

Укажите физическую особенность течения через насадок?

2. возникает вакуум внутри насадка

Укажите чему равна наименьшая длина насадка?

Укажите числовое значение коэффициента скорости при истечение из насадка?

Укажите числовое значение коэффициента расхода при истечение из насадка?

Укажите причину возрастании коэффициента расхода при истечение через насадок по сравнению с истечением через отверстие?

3. отсутствие сжатия струи в насадке

Укажите причину возрастании коэффициента расхода при истечение через насадок по сравнению с истечением через отверстие?

2. возникновения вакуума

Укажите числовое значение коэффициента сопротивления внешнего цилиндрического насадка?

Как соотносятся коэффициенты скорости насадка и отверстии при одинаковых числах Рейнольдса?

3. коэффициент скорости насадка меньше чем коэффициент скорости отверстии

Как соотносятся коэффициенты расхода насадка и отверстия при одинаковых числах Рейнольдса?

1. коэффициент расхода для насадка больше чем для отверстия

Как соотносятся коэффициенты сопротивления насадка и отверстия при одинаковых числах Рейнольдса?

2. коэффициент сопротивления насадка больше коэффициента сопротивления отверстия

В какую энергию превращается часть механической энергии потока, теряющаяся в насадке?

4. в тепловую энергию

Укажите условие существования вакуума?

2. абсолютное давление меньше атмосферного

Укажите количественную характеристику величины вакуума?

1. разность между атмосферным и абсолютным давлением

Укажите чему равно значение наибольшей величины вакуума?

2. атмосферному давлению

Укажите чему равно значение наибольшей величины вакуума?

2. 10 метрам водяного столба

Укажите чему равен критический напор для внешнего цилиндрического насадка?

4. 13 метрам водяного столба

Как изменяется расход воды через насадок при срыве вакуума?

Как изменяется скорость истечения через насадок при срыве вакуума?

Как изменяется дальность отлета струи при срыве вакуума в насадке?

Как изменяется диаметр струи при срыве вакуума в насадке?

Как соотносятся между собой потери на трение и местные потери в коротком трубопроводе?

3. потери на трение значительно меньше местных потерь

Укажите причину значительного увеличения потерь напора при истечение через насадок по сравнению с отверстием?

2. вихреобразование при расширение струи

Истечение из отверстия

Какое отверстие в стенке цилиндрического резервуара считается малым? 4. если диаметр отверстия мал по сравнению с напором

В каком случае при истечении из отверстия в стенке резервуара, стенка считается тонкой?

4. если толщина стенки меньше 3 диаметров отверстия

Какие силы вызывают сжатие струи при истечении из отверстия?

3. центробежная сила

Укажите используемое определение коэффициента сжатия струи, истекающей из отверстия в стенке цилиндрического резервуара?

4. отношение площади сжатого сечения к площади отверстия

Укажите, какое преобразование энергии происходит при истечении идеальной жидкости из отверстия в стенке резервуара?

2. потенциальная энергия жидкости в резервуаре превращается в кинетическую

Какое отверстие в стенке цилиндрического резервуара считается большим?

1. если размер отверстия более 0,1 от напора

Источник

Потери энергии в местных сопротивлениях

Изменение характеристик потока жидкости, таких как скорость, направление движения, расход за счет слияния или разделения потоков и т.п., приводит к потерям энергии (напора, давления). Поскольку указанные изменения происходят на коротком участке, то такие потери называют местными. Элементы трубопроводов, в которых наблюдаются местные потери энергии, называют местными сопротивлениями. К ним относят: клапаны, краны, всевозможные регуляторы расхода и давления, золотники, колена, тройники, фильтры и т.п.

Аналитическое определение местных потерь энергии возможно только в некоторых простейших случаях. Для практических расчетов используют формулу Дарси

, (1.51)

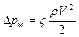
где 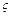– коэффициент местных потерь, определяемый экспериментальным путем.

Потери энергии при внезапном расширении потока

Примером аналитического определения местных потерь энергии является задача о внезапном расширении движущейся жидкости.

Рассмотрим поток, движущийся со скоростью V₁ в круглой цилиндрической трубе, площадь поперечного сечения которой равна S₁. При внезапном увеличении площади трубы до величины S₂ струя жидкости постепенно заполнит все поперечное сечение большей трубы, и на некотором расстоянии от места расширения установится течение со скоростью V₂ р₁). Повышение давления связано с уменьшением скорости потока. Это справедливо как для идеальной, так и для реальной жидкостей. В реальной жидкости повышение давления несколько ниже, чем в идеальной, из-за потери энергии потока в вихрях, возникающих в результате проявления вязкости.

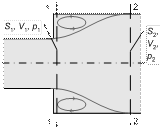
Для определения разности давлений в сечениях 1-1 и 2-2 воспользуемся уравнением изменения количества движения (уравнением импульса), согласно которому изменение количества движения потока во времени равно главному вектору приложенных к нему внешних сил. Изменение количества движения за единицу времени можно представить следующим выражением

.

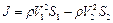
Внешней силой, приложенной к выделенному объему, является сила, возникающая в результате разности давлений, действующих на торцевые поверхности

.

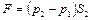
Приравнивая эти выражения, получим

.

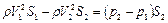
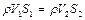
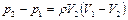
Принимая во внимание, что массовый расход жидкости постоянен, , последнее уравнение преобразуется к виду

.

При внезапном расширении идеальной жидкости, изменение давления между рассматриваемыми сечениями определяется на основании уравнения Бернулли

.

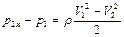
Разность этих уравнений дает потерю энергии, обусловленную вязкостью жидкости, которая превращается в теплоту

.

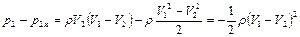
Полученное выражение получило название формулыБорда. Ее можно преобразовать к виду, соответствующему уравнению Дарси,

.

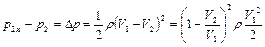
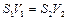
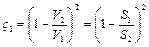
Первый сомножитель в правой части уравнения представляет собой коэффициент местного сопротивления при внезапном расширении, который, с учетом уравнения неразрывности ( ), можно представить в следующем виде

.

Дата добавления: 2015-01-24 ; просмотров: 1384 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

В какую энергию превращается энергия потерянная потоком в местном сопротивлении

9. МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

9.1. Общие сведения о местных сопротивлениях

9.2. Внезапное расширение трубопровода

9.3. Постепенное расширение трубы

9.6. Местные сопротивления при ламинарном течении

9.1. Общие сведения о местных сопротивлениях

Потери энергии (напора) состоят из потерь на трение по длине и потерь в местных гидравлических сопротивлениях.

Местными сопротивлениями называются участки трубопроводов, на которых из-за изменения размеров или конфигурации русла происходит деформация потока и изменения значения или направления скоростей движения жидкости, при этом возникают отрыв потока от стенок трубы и вихреобразования.

К таким сопротивлениям относятся: вентили, диафрагмы, внезапные расширения и сужения, колено, поворот на некоторый угол и другие.

Потери энергии, отнесенные к единице веса потока жидкости подсчитывают формуле (Вейсбаха-Дарси):

Сложные случаи местных сопротивлений это соединения или комбинации сопротивлений. Так, например, при течении жидкости через вентиль поток искривляется, меняет своё направление, сужается и, наконец, расширяется до первоначальных размеров, при этом возникают интенсивные вихреобразования

Значения коэффициентов местных сопротивлений в большинстве случаев получают из опытов, на основании которых составляют таблицы или строят графики. Для некоторых случаев эти коэффициенты могут быть получены теоретически.

9.2. Внезапное расширение трубопровода

При внезапном расширении трубы (рис. 1.63) поток расширяется до большего диаметра не сразу, жидкость отрывается от стенок и дальше движется в виде свободной струи, отделенной от остальной жидкости поверхностью раздела. Поверхность раздела неустойчива, в кольцевом пространстве между потоком и стенкой трубы образуются вихри. Струя постепенно расширяется, пока на некотором расстоянии l от начала расширения не заполняет все сечение «2-2» трубы

.

Прежде чем составлять исходные уравнения, сделаем три допущения:

1) распределение скоростей в сечениях 1-1 и 2-2 равномерное; т. е. α₁ = α₂ = 1, что обычно принимается при турбулентном режиме.

2) учитывая, что участок 1-2 невелик, силами трения пренебрегаем;

(9.1)

«Сила, действующая на тело равна изменению количества движения тела за единицу времени».

Соответствующее изменение количества движения является разностью между секундным количеством движения, выносимым из рассматриваемого объема и вносимым в него:

(9.4.),

Сгруппировав члены, получим

По уравнению расхода

полученный результат можно выразить относительно скорости V 1 в узкой трубе, в сечении «1-1»:

(9.5)

Коэффициент потерь для внезапного расширения трубопровода:

(9.6)

Формула хорошо подтверждается опытом при турбулентном течении и широко используется в расчетах.

Когда площадь S _2, весьма велика по сравнению с площадью S ₁ и, следовательно, скорость V ₂ можно считать равной нулю, потеря на расширение

Т. е. в этом случае теряется весь скоростной напор (вся кинетическая энергия, которой обладает жидкость); коэффициент потерь ξ = 1.

Такому случаю соответствует, например, подвод жидкости по трубе к резервуару достаточно больших размеров.

9.3. Постепенное расширение трубы

Местное сопротивление, при котором труба расширяется постепенно, называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, а, следовательно, преобразование кинетической энергии жидкости в энергию давления. Частицы движущейся жидкости преодолевает нарастающее давление за счет своей кинетической энергия, которая уменьшается вдоль диффузора в том числе и направлении от оси к стенке. Слои жидкости, прилежащие к стенкам, обладают столь малой кинетической энергией, что иногда оказываются не в состоянии преодолевать повышенное давление, они останавливаются или даже начинают двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразование (рис.9.2). Интенсивность этих явлений возрастает с увеличением угла расширения диффузора, а вместе с этим растут и потери на вихреобразование в нем.

Кроме того, в диффузоре имеются потери на трение.

Полную потерю напора в диффузоре условно найдем, как сумму двух слагаемых:

где h _тр и h _п.р. — потери напора на трение и расширение (на вихробразование)

Потерю напора на трение можно приближенно подсчитать следующим способом. Рассмотрим круглый диффузор с прямолинейной образующей и с углом α при вершине.

Пусть радиус входного отверстия диффузора равен r ₁, выходного r ₂ (рис.9.3). Так как радиус сечения и скорость движения жидкости являются переменными вдоль диффузора, то следует взять элементарный отрезок диффузора длиной dl вдоль образующей и для него выразить элементарную потерю напора на трение по основной формуле

Из элементарного треугольника следует: dl = dr / Sin ( α /2).

Подставим эти выражения в формулу для dh _ТР и выполним интегрирование в пределах от r ₁ до r ₂, т.е. вдоль всего диффузора, считая при этом коэффициент λ_Т – постоянным:

Откуда, после интегрирования получим

(9. 8)

Потеря напора на расширение имеет в диффузоре ту же природу, что и при внезапном расширении. Поэтому определяется по формуле Борда с поправочным коэффициентом k _п.р. меньшим единицы и называемым также коэффициентом смягчения.

(9. 9)

Учитывая полученные формулы (9.8) и (9. 9) можно исходное выражение (9. 7) переписать в виде

(9.11)

А коэффициент сопротивления диффузора можно выразить формулой

(9.12)

Важно выяснить характер зависимости ξ_диф от угла α. С увеличением угла α при заданных λ_т и n первое слагаемое в формуле (9.12), обусловленное трением, уменьшается, так как диффузор становится короче, а второе слагаемое, обусловленное вихреобразованием и отрывом потока, увеличивается. При уменьшении же угла α вихреобразование уменьшается, но возрастает трение, так как при заданной степени n расширения диффузор удлиняется, и поверхность его трения увеличивается.

Функция ξ_диф = f ( α) имеет минимум при некотором наивыгоднейшем оптимальном значении угла α (рис.9.4).

Для сокращения длины диффузора при заданном n обычно принимают несколько большие углы, а именно 7 ÷ 9°. Эти же значения угла можно рекомендовать и для прямоугольных диффузоров.

Для прямоугольных диффузоров с расширением в одной плоскости (плоские диффузоры) оптимальный угол больше, чем для круглых и квадратных, и составляет 10 ÷ 12°.

Если габариты не позволяют установить углы α близкие к оптимальным, то при

α > 15 ÷ 25° целесообразно отказаться от диффузора с прямолинейной образующей и применить один из специальных диффузоров, например, диффузор, обеспечивающий постоянный градиент давления вдоль оси dp / dx = const и, следовательно, приблизительно равномерное нарастание давления (при прямой образующей градиент давления убывает вдоль диффузора) (рис.9.5б).

Уменьшение потери энергии в таких диффузорах по сравнению с обычными будет тем больше, чем больше угол α, и при углах 40 — 60° доходит до 40 % от потерь в обычных диффузорах. Кроме того, поток в криволинейном диффузоре отличается большей устойчивостью, т. е. в нем меньше тенденций к отрыву потока. Хорошие результаты дает также ступенчатый диффузор, состоящий из обычного диффузора с оптимальным углом и следующего за ним внезапного расширения.

9.4. Сужение трубопровода

Внезапное сужение трубы (рис.9.6) всегда вызывает меньшую потерю энергии, чем внезапное расширение с таким же соотношением площадей. В этом случае потеря обусловлена, во-первых, трением потока при входе в узкую трубу и, во-вторых, потерями па вихреобразование. Последние вызываются тем, что поток не обтекает входной угол, а срывается с него и сужается. Кольцевое же пространство вокруг суженной части потока заполняется завихренной жидкостью.

В процессе дальнейшего расширения потока происходит потеря напора

(9.13)

Для практических расчетов можно пользоваться полуэмпирической формулой Идельчика:

Из формулы следует, что в том частном случае, когда можно считать S ₂/ S ₁= 0, т.е. при выходе трубы из резервуара достаточно больших размеров и при отсутствии закруглений входного угла, коэффициент сопротивления

Закруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе в трубу.

Постепенное сужение трубы, т. е. коническая сходящаяся труба, называется конфузором (рис.9.7). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления, так как давление жидкости в начале конфузора выше, чем в конце, причин к возникновению вихреобразований и срывов потока, как в диффузоре, нет. В конфузоре имеются лишь потери на трение. В связи с этим сопротивление конфузора всегда меньше, чем сопротивление такого же диффузора.

Потерю напора на трение в конфузоре можно подсчитать так же, как это делали для диффузора, т. е. сначала выразить потерю для элементарного отрезка, а затем выполнить интегрирование. В результате получим следующую формулу:

(9.15)

Потери на вихреобразование определяются по формуле

Кпс. при 40 градусах равен 0,2. при осмтаьных значениях угла он увеличивается. Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора вместе соединения конической трубы с цилиндрической. Для ликвидации вихреобразования и связанных с ним потерь рекомендуется коническую часть плавно сопрягать с цилиндрической или конической частью заменять криволинейной, плавно переходящей в цилиндрическую (рис.(9.16).

При этом можно допустить значительную степень сужения n при небольшой длине вдоль оси и небольших потерях.

1. Внезапный поворот трубы, или колено без закругления (рис. 9.17), обычно вызывает значительные потери энергии, так в нем происходят отрыв потока и вихреобразование, причем эти потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

Коэффициент сопротивления колена круглого сечения ξ _кол возрастает с увеличением δ очень круто (рис.9.17) и при δ = 90° достигает единицы.

Для отводов круглого сечения с при турбулентном течении можно пользоваться эмпирической формулой, которая для отводов является основной:

Для углов меньше δ

9.6. Местные сопротивления при ламинарном течении

Изложенное в предыдущих параграфах данной главы, относилось к местным гидравлическим потерян при турбулентном режиме течения в трубопроводе. При ламинарном режиме, во-первых, местные сопротивления обычно играют малую роль по сравнению с сопротивлением трения и, во-вторых, закон сопротивления является более сложным и исследован в меньшей степени, чем при турбулентном течении.

Учитывая закон сопротивления при ламинарном течении, выражении и λ_л =64/ Re с поправкой на начальный участок, а также формулу

h _м = ζм V 2 /(2 g ), выражение (1.119) можно представить в виде:

где А и В — баразмерные коэффициенты, зависящие в основном от формы местного сопротивления.

После деления уравнения (1.119) на скоростной напор получим общее выражение для коэффициента местного сопротивления при ламинарном течении в трубопроводе

В таких местных сопротивлениях, где имеется узкий канал, длина которого значительно превышает его поперечный размер с плавными очертаниями входа и выхода, как, например, показано на рис. 1.76а, и числа Re малы, потеря напора определяется в основном трением, и закон сопротивления близок к линейному.

Второй член в формулах (1.119) и (1.120) в этом случае равен нулю или очень мал по сравнению с первым.

Если же в местном сопротивлении трение сведено к минимуму, например, благодаря острой кромке, как на рис. 176б, и имеются отрывы потока и вихреобразование, а числа Re достаточно велики, то потери напора пропорциональны скорости и расходу приблизительно во второй степени.

Иногда вместо двучленной формы выражения местных гидравлических потерь применяют степенной одночлен.

где k размерная величина, m — показатель степени, зависящий от формы местного сопротивления и Re и изменяющийся d пределах от 1 до 2.

Тогда суммарное значение потерь на трение увеличится на величину l _экв

Численные значения эквивалентных длин (отнесенных к диаметру трубопровода) для различных местных сопротивлений обычно находят опытным путем.

Как показывают экспериментальные исследования, коэффициент потерь для внезапного расширения

Когда по трубе подводится жидкость со скоростью V ₁ к резервуару больших размеров, где V ₂ = 0, то можно считать, что теряется вся удельная кинетическая энергия жидкости, которая для стабилизированного ламинарного потока в круглой трубе равна

Причем коэффициент Кориолиса α _л тем больше, чем больше число Re и чем более удален от входа в трубу расчетный участок.

Если же поток не является стабилизированным, длина трубы l l нач, то коэффициент α _л следует определять по графику, данному на рис. 1.46.

Источник