в какую фигуру нельзя вписать окружность
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
\[ S = \frac<1><2>(a+b+c) \cdot r = pr \]
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
\[ S = \frac<1><2>(a+b+c+d)\cdot r = pr \]
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Описанная окружность
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
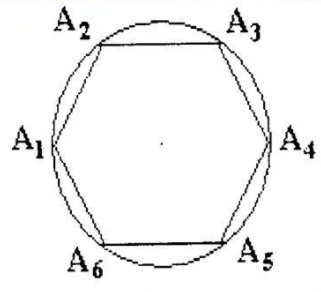
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.
Вписанная окружность
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.
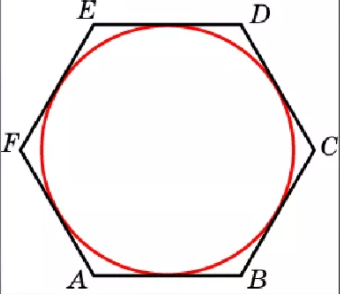
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.
Вписанный и описанный треугольники
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
В любой треугольник можно вписать окружность: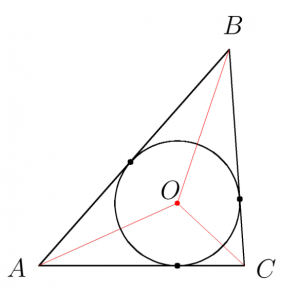 
Центр вписанной окружности
Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Вписанный и описанный четырехугольники
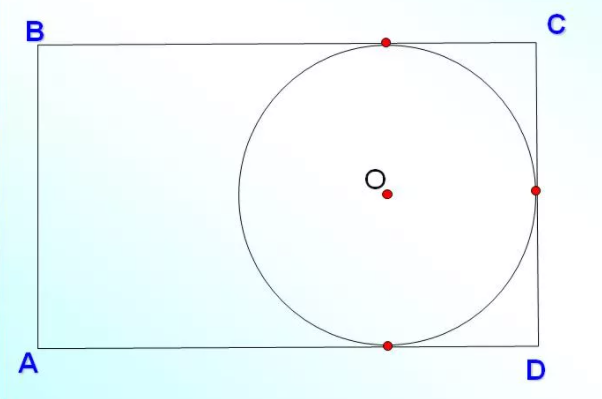
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.
Условие вписанной в 4-х угольник окружности
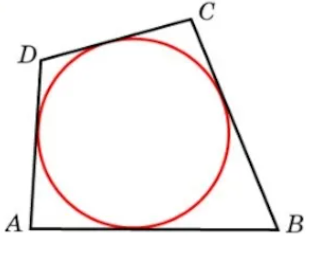
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.
На рисунке выполняется данное условие, то есть AD + BC=DC + AB
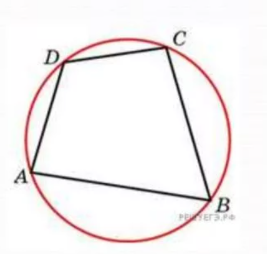
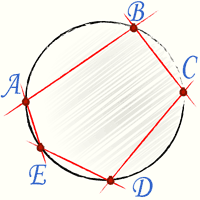
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.
На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.
Геометрический тест: как хорошо вы знаете математику?
Какой из этих ученых не имеет отношения к геометрии?
Численная величина, которая характеризует размер фигуры
Сумма длины всех сторон
Вместимость области пространства
Все фигуры имеют одинаковый периметр. Какая из них имеет наибольшую площадь?
Какая фигура изображена на картинке?
Как называется эта геометрическая фигура?
Какое геометрическое тело изображено на картинке?
Сумма всех углов треугольника составляет.
Формула Герона используется для.
Вычисления площади треугольника
Вычисления площади прямоугольника
Вычисления площади ромба
В какую фигуру нельзя вписать окружность?
Линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Часть прямой, которая ограничена двумя точками
Часть прямой, которая имеет начало, но не имеет конца
Отношением противолежащего катета к гипотенузе называется.
Как называется утверждение, требующее доказательства?
Поздравляем! Вы закончили проходить геометрический тест! Расскажите друзьям о своем результате!
Дебютный снимок Земли из космоса был сделан ещё в 1946 году — за десять лет до того, как первый спутник вышел в безвоздушное пространство. Как сделали фотографию? Очень просто. Запустили фотокамеру на ракете «Фрау-2». Устройство достигло отметки 105 километров, сделало несколько снимков, прежде, чем развалиться на части. Конечно, по качеству те фотографии с современными не сравнить.Чёткость современных снимков невероятная. Вы можете рассмотреть не только очертания континентов, но и яркую подсветку городов. Поможет ли вам высокое разрешение правильно определить страну по её космической фотографии?
С грамотным и образованным человеком всегда приятно вести беседу. Но искусство общения требует постоянной практики и не всем дается легко. Кто умеет правильно и грамотно говорить и писать, тот всегда желанный гость на всех мероприятиях. Каков уровень твоей грамотности и образования, как хорошо ты знаешь русский язык? Проверь себя!
Чтобы выжить за границей, не обязательно быть полиглотом. Сегодня, зная разговорный английский, вы запросто объяснитесь в любом уголке мира, особенно в Европе. Большинство преподавателей дают своим ученикам узкую, профессиональную лексику, которая в реальной жизни не поможет. Давай проверим, на каком уровне находится твой разговорный английский и сможешь ли ты с ним путешествовать по миру.
Чтобы ответить на вопросы этого теста недостаточно знать географию; твой кругозор должен быть широким, знания – великолепными, а зрительная память – отличной. Если сможешь ответить хотя бы на 8 из 10 вопросов, то твоей эрудиции можно позавидовать. Проверь себя и свои знания. Поехали!
Современного человека не просто удивить, особенно в интернете. Кажется, что все удивительные факты уже разошлись по глобальной сети. Однако мы заметили, что это практически не задело литературу, поэтому решили восстановить справедливость. Пройди наш тест и попробуй отгадать, где правда, а где вымысел.
Фразеологизмы – это крылатые выражения, не имеющие автора. Эти «изюминки» прочно вошли в наш язык, и воспринимаются как естественный элемент речи, идущий от народа, из глубины веков. Пройди тест, получи новую порцию знаний, придай своим выражениям эмоциональную окраску.
Встречают по одежке, а провожают по уму. Поэтому, путешествуя по миру, стоит не забыть заглянуть в словарик и узнать, к кому же вы на самом деле едете в гости. Пройди тест и узнай, как правильно называть жителей стран мира.
На Земле есть города, которые сконцентрировали в себе что-то очень притягательное. Миллионы туристов каждый год собирают чемоданы, чтобы увидеть их своими глазами. Предлагаем сыграть в игру и попробовать угадать, каким городам принадлежат названные факты. Поехали!
Древняя и в то же время современная, экзотическая и удивительная, уникальная страна с богатой историей – Турция. Здесь сочетаются культура Европы и Азии. Именно сюда чаще всего стремятся люди, чтобы провести свой отпуск. Мечети, пляжи, горы, термальные источники – это не весь список достоинств страны. А что знаешь о Турции ты? Проверь себя.
Современному человеку необходимо быть в курсе всех событий, в том числе и политических. Ситуация в мире довольно напряжённая, и решения о её урегулировании принимают именно главы государств. Проверим, что ты о них знаешь!
Если вы хорошо учились в школе, то вам не составит труда пройти этот тест с высоким результатом. Учитывая то, что сейчас большой процент общения приходится на социальные сети и мессенджеры, крайне важно писать грамотно. Если ваш собеседник образован, он обязательно обратит на это внимание. Начнём же проверку!
Выбрать в качестве профессии писательство может только человек особенный, который сознательно подвергает себя на серьезные физические и душевные мучения. Достоевский говорил, что, единожды издав поэму или роман, у автора есть только два пути: писать или застрелиться. Сможешь ли ты определить какой пагубной привычкой страдала та или иная известная личность?
В русском языке много правил, исключений и просто непонятных вещей. Сегодня мы предлагаем разобраться с «не» и «ни». Знаешь ли ты, где и как они употребляются? Сейчас проверим!
Считаете себя знатоком географии? Тогда назовите без подсказки самую большую пустыню Евразии. И заодно вспомните, какой пролив разделяет Евразию и Америку. На эти вопросы среднестатистический школьник ответит, если подумает. Вы уже, скорее всего, позабыли большую часть базового материала. Мы подобрали интересные вопросы из школьной программы по географии и предлагаем вам проверить свои знания. Немногие врослые справляются с тестом. Давайте узнаем, кто умнее — вы или среднестатистический школьник. Не надейтесь, что вопросы будут легкими.
Собор Парижской Богоматери — самое популярное среди туристов место Парижа. Писатели посвящали ему романы, а верующие называют место святым. В этом году собор прославился на весь мир, к сожалению, в связи с печальными обстоятельствами: случайный пожар разрушил большую часть здания. На протяжении пяти лет храм будет закрыт, его ждет масштабная реставрация. И если в ближайшие годы посетить его не удастся, то узнать больше об этой достопримечательности ничто не мешает. Давайте проверим, что вы знаете о соборе Парижской Богоматери!
Вписанные и описанные многоугольники
Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.
Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.
 Вписанный многоугольник | 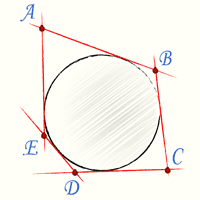 Описанный многоугольник |
Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.
Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них
Для треугольника всегда возможны и вписанная окружность и описанная окружность.
Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.
Правильные многоугольники
Итак, слово «правильный» в условии задачи сразу говорит нам о том, что все стороны и все углы многоугольника одинаковые. Количество углов (вершин) и количество сторон определяем по названию многоугольника. Далее в формулах и задачах будем обозначать это количество символом n.
и так далее.
правильный пятиугольник.
Чтобы построить другие правильные многоугольники, задайте количество сторон n (от 3-ёх до 12-ти).
Многоугольники можно вписывать в окружность или описывать вокруг неё. Однако, это получается не для всех и не всегда. Говоря математическим языком, не всегда существует окружность, которая удовлетворяет определению.
Четырехугольник вписан в окружность.
Четырехугольник описан около окружности.
Рассмотрим другие примеры.
Параллелограмм нельзя вписать в окружность. Описать можно только ромб.
В окружность можно вписать только равнобочную трапецию, описать около окружности тоже можно не всякую трапецию.
Существование вписанной и описанной окружности для произвольных многоугольников связано с величинами их углов и сторон. Есть специальные теоремы, позволяющие определить будет ли многоугольник являться вписанным и/или описанным. Сейчас мы на них останавливаться не будем. Сейчас важно отметить следующее:
Треугольник вписан в зеленую окружность, описан вокруг синей.
Пятиугольник вписан в зеленую окружность, описан вокруг синей.
Правильные многоугольники имеют центр, точнее совпадающие в одной точке центр симметрии, центр тяжести, центры вписанной и описанной окружностей. Если соединить с центром правильного n-угольника его вершины, то многоугольник разобьется на n равных равнобедренных треугольников.
При решении задач на правильный многоугольник, часто бывает удобно дорисовать внешнюю (описанную) или внутреннюю (вписанную) окружность даже, если они не упоминаются в условии, и соединить вершины и точки касания с центром. Получатся равнобедренные или прямоугольные треугольники, о которых много известно, поэтому задачу будет решать легко.
Синие треугольники равнобедренные потому, что их боковые стороны это радиусы одной и той же окруюности.
Оранжевые треугольники прямоугольные потому, что касательная к окружности перпендикулярна её радиусу.
На ОГЭ по математике в 9-ом классе и на ЕГЭ в 11-ом встречаются задачи с правильными многоугольниками, часто они включают в себя и вписанную или описанную окружность.
Задачи на правильные многоугольники
Внимание: задачи с решениями, но они временно скрыты. Сначала сделайте попытку решить задачу самостоятельно, и только после этого нажимайте кнопки «Посмотреть ответ» и «Посмотреть решение». Cовпадать обязан только ответ. Способ решения может отличаться.
Ответ: S = pr
Примечание: Отношение сторон многоугольников можно найти иначе, например, достроить другие внутренние отрезки и рассмотреть прямоугольные треугольники.
Ответ: 85
В круг вписан правильный шестиугольник ABCDEF. Найти площадь круга, если радиус окружности, вписанной в треугольник ADE, равен r.
Определим площадь треугольника ADE двумя способами:
через произведение катетов \[S = \frac<
Ответ: 2πr 2 (2 + √3 _ )
Найти отношение площади правильного двадцатичетырёхугольника, вписанного в некоторую окружность, к площади правильного двенадцатиугольника, вписанного в ту же окружность.
Ответ: 4sin15° ≈ 1,04
Примечание: Если Вы не догадались использовать свойство медиан треугольника, то можно рассматривать треугольники AOC, AOH и т.п., теорему косинусов или теорему Пифагора. Ответ будет получен с чуть большим объёмом вычислений.
Ответ: 7