в какую тоновую качественную величину при обращении переходят увеличенные интервалы ответ
Увеличенные и уменьшенные интервалы: как их построить?
Вы знаете, что интервалы бывают чистыми, малыми и большими, но также они могут быть увеличенными и уменьшенными, а кроме того – дважды увеличенными и дважды уменьшенными. Но как такие интервалы получить, как их построить и определить? Об этом мы сегодня и поговорим.
Предыдущие важные темы:
ЧТО ТАКОЕ ИНТЕРВАЛЫ И КАКИЕ ОНИ БЫВАЮТ – ЧИТАТЬ ЗДЕСЬ
КОЛИЧЕСТВЕННАЯ И КАЧЕСТВЕННАЯ ВЕЛИЧИНА ИНТЕРВАЛА – ЧИТАТЬ ЗДЕСЬ
Что такое увеличенные и уменьшенные интервалы?
Увеличенные интервалы получаются, если прибавить полтона к чистому или большому интервалу, то есть если немного изменить качественную величину. Увеличить можно все интервалы – от примы до октавы. Сокращенный способ обозначения таких интервалов – «ув».
Давайте сравним в следующей таблице количество тонов и полутонов в обычных интервалах, то есть чистых и больших, и в увеличенных.
Таблица — Качественная величина чистых, больших и увеличенных интервалов
| Исходный интервал | Сколько тонов | Увеличенный интервал | Сколько тонов |
| ч.1 | 0 т. | ув.1 | 0,5 т. |
| б.2 | 1 т. | ув.2 | 1,5 т. |
| б.3 | 2 т. | ув.3 | 2,5 т. |
| ч.4 | 2,5 т. | ув.4 | 3 т. |
| ч.5 | 3,5 т. | ув.5 | 4 т. |
| б.6 | 4,5 т. | ув.6 | 5 т. |
| б.7 | 5,5 т. | ув.7 | 6 т. |
| ч.8 | 6 т. | ув.8 | 6,5 т. |
Уменьшенные интервалы, наоборот, возникают при сужении чистых и малых интервалов, то есть при уменьшении их качественной величины на полтона. Уменьшить любой интервал, кроме чистой примы. Дело в том, что в приме – ноль тонов, из которых больше ничего не вычтешь. Сокращенно уменьшенные интервалы записываются как «ум».
Для большей наглядности также построим таблицу со значениями качественной величины для увеличенных интервалов и их прототипов: чистых и малых.
Таблица — Качественная величина чистых, малых и уменьшенных интервалов
| Исходный интервал | Сколько тонов | Уменьшённый интервал | Сколько тонов |
| ч.1 | 0 т. | нет | нет |
| м.2 | 0,5 т. | ум.2 | 0 т. |
| м.3 | 1,5 т. | ум.3 | 1 т. |
| ч.4 | 2,5 т. | ум.4 | 2 т. |
| ч.5 | 3,5 т. | ум.5 | 3 т. |
| м.6 | 4 т. | ум.6 | 3,5 т. |
| м.7 | 5 т. | ум.7 | 4,5 т. |
| ч.8 | 6 т. | ум.8 | 5,5 т. |
Как строить увеличенные и уменьшенные интервалы?
Чтобы построить любой увеличенный и уменьшенный интервал, проще всего представить себе его «исходник», то есть большой, малый или чистый интервал и просто что-то в нем изменить (сузить его или расширить).
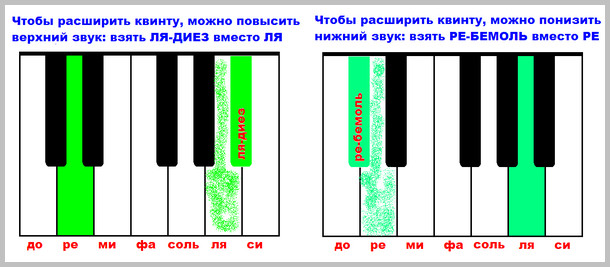
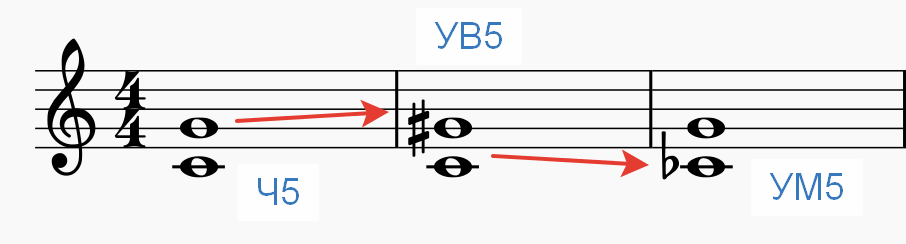
Как можно расширить интервал? Для этого можно либо его верхний звук повысить с помощью диеза на полтона, либо нижний спустить с помощью бемоля. Очень наглядно это видно, если взять интервал на клавиатуре фортепиано. Давайте для примера возьмем чистую квинту РЕ-ЛЯ и посмотрим, как ее можно увеличить:
Какие результаты получились? Увеличенная квинта от исходной чистой – это либо РЕ и ЛЯ-ДИЕЗ, либо РЕ-БЕМОЛЬ и ЛЯ, в зависимости от того, какой звук мы выбрали изменить. Кстати, если мы изменим сразу оба звука, то квинта станет дважды увеличенной, то есть расширится сразу на два полутона. Посмотрите, как эти результаты выглядят в нотной записи:
Как можно сузить интервал? Нужно действовать наоборот, то есть сворачивать его внутрь. Для этого мы либо верхний звук теперь уже понижаем на полтона или, если манипулируем нижним звуком, т о его повышаем, немного приподнимаем. В качестве примера рассмотрим ту же самую квинту РЕ-ЛЯ и попробуем ее сузить, то есть уменьшить.
Чего мы добились? Была чистая квинта РЕ-ЛЯ, мы получили два варианта уменьшенной квинты: РЕ и ЛЯ-БЕМОЛЬ, РЕ-ДИЕЗ и ЛЯ. Если изменить сразу оба звука квинты, то выйдет дважды уменьшенная квинта РЕ-ДИЕЗ и ЛЯ-БЕМОЛЬ. Смотрим нотный пример:
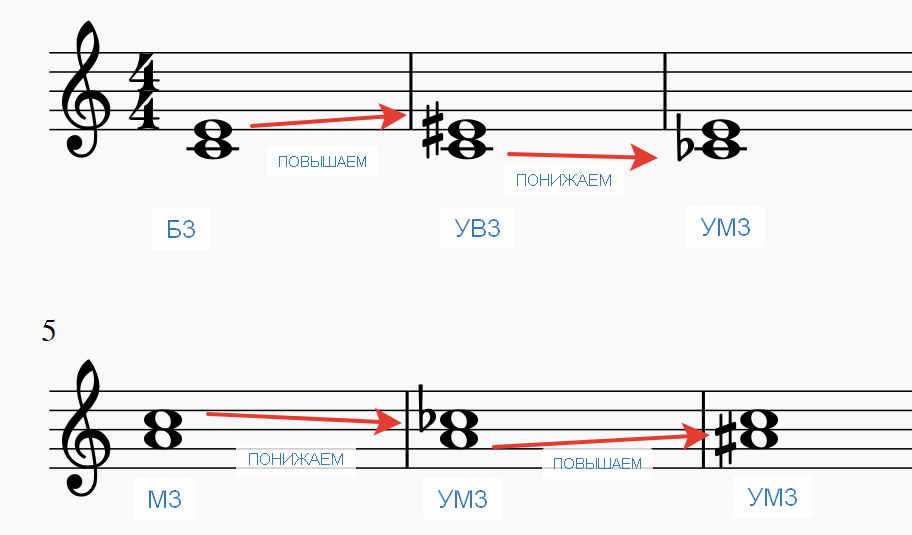
Посмотрите, что можно сделать с другими интервалами. Сейчас перед вами четыре нотных примера. Сравните их и понаблюдайте, как из одних интервалов получаются другие, путем манипулирования верхним звуком – он то повышается, то понижается на полтона.
Пример 1. Чистые и большие интервалы от РЕ, построенные вверх
Пример 2. Увеличенные интервалы от РЕ вверх
Пример 3. Чистые и малые интервалы от РЕ, построенные вверх
Пример 4. Уменьшенные интервалы от РЕ вверх
Энгармонизм интервалов
Зачем мы об этом вообще завели разговор? Вы, когда рассматривали таблицу с количеством тонов в начале статьи, когда потом смотрели наши примеры, наверное, удивлялись: «Как это в увеличенной приме может быть полтона, ведь полтона – в малой секунде?» или «Что еще за РЕ-ЛЯ-ДИЕЗ, напиши РЕ-СИ-БЕМОЛЬ и получится у тебя нормальная малая секста, зачем все эти увеличенные квинты?». Были такие мысли? Признайтесь, что были. Это как раз и есть примеры энгармонизма интервалов.
Давайте посмотрим больше примеров энгармонизмов. Возьмем те же интервалы от РЕ. Увеличенная секунда звучит как малая терция, большая терция равна уменьшенной кварте, увеличенная кварта совпадает с уменьшенной квинтой и т.д.
Строить увеличенные и уменьшенные интервалы несложно тому, кто хорошо научился строить обычные интервалы. Поэтому, если у вас имеются пробелы в практике, то срочно их ликвидируйте. На этом все. В следующих выпусках мы будем говорить о консонансах и диссонансах, о том, как звучат гармонические и мелодические интервалы. Ждем вас в гости!
Увеличенные и уменьшенные интервалы (Характерные интервалы)
В этой статье рассмотрим основные особенности и характеристику увеличенных интервалов и научимся их строить, как в тональности, так и от произвольного звука.
Вспомним, что интервал это расстояние между двумя звуками или если выразиться более научно это соотношение или сочетание двух звуков. Для того, что бы найти интервал от любого звука нам нужно пройти определенное расстояние, которое мы измеряем по 2 параметрам:
Сколько шагов по диатонике ( то есть по нотам CDEFGAB) нужно сделать, чтобы перейти от одной ноты до другой. Например, есть интервал CA между этими звуками находится еще 5 нот (белых клавиш на фортепиано) — это звуки DEFG. Получается, что всего мы делаем 6 шагов CDEFGA. Шесть шагов дают интервал сексты (шесть — секст).
Сколько полутонов и тонов в одном интервале. Если бы расстояние между всеми звуками диатоники было равным, то и интервалы были бы однозначными, но так как между звуками EF и BC расстояние в полтона, то даже одно и тоже расстояние по шагам будет неравнозначным по количеству тонов или полутонов. Например, сделаем 6 шагов от звука D (EFGA) B – получили интервал DB это тоже секста, как и в предыдущем примере. Но расстояние от ноты C до ноты A = 4, 5 тонам, а расстояние от D до B = 4 тонам. Получается, что если мы скажем секста от ноты С и секста от ноты D, то это будет лишь частичная информация о расстоянии, так как она не содержит указаний на количество тонов или полутонов. Поэтому мы говорим, что секста CA большая или мажорная, так как она строится на первой ступени мажорного лада, а секста DB малая или минорная.
Как появляются увеличенные или уменьшенные интервалы?
Здесь нет ничего сложного. Причина появления этих интервалов опять же в точности обозначения ступеневого и тонового соотношения (величины) интервалов.
Например, если мы возьмем такое соотношение звуков F – G# и попробуем посчитать, что это за интервал, то получим следующее.
Считаем сколько шагов мы делаем. FG это 2 шага, то есть интервал секунда.
Считаем количество тонов — оно равно 1,5 тона
То есть по ступеням это интервал секунда, а по количеству тонов интервал малой терции. Получается, что этот интервал больше на полтона чем большая секунда FG. Такой интервал мы называем увеличенным.
Явление при котором интервалы имеют одинаковую тоновую величину, но разное количество ступеней называется энгармонизмом интервалов, а сами интервалы называются энгармоническими.
Некоторые могут спросить, а зачем записывать это как FG#, если можно записать как FAb и получить малую терцию? Такой вопрос, как правило, связан с непониманием природы тональности.
Например, интервал FG# возможно получить в тональности Am, но ноты Ab в тональности Am нет и быть не может, так как незыблемое правило гласит — тоника изменятся не может, так как мы получим другую тональность. Кроме того, интервал увеличенной секунды в мелодии звучит не также, как интервал малой терции, что объясняется свойством ступеней лада, а также напоминает о дотемперированой эпохе музыкального строя.
Итак, если интервал больший чем большая секунда мы называем увеличенным, то отсюда делаем простой вывод интервал меньший чем малый мы называем уменьшенным.
Например, малая терция AC, а ACb будет уменьшенной терцией. То есть для того, чтобы получить увеличенный интервал нам нужно поднять на полтона верхний звук, без изменения его названия или понизить нижний, а для получения уменьшенного понизить верхний или повысить нижний.
Кроме малых и больших интервалов у нас есть еще чистые. Для них все еще проще. Повышая чистый интервал мы получаем увеличенный, понижая уменьшенный.
Повышая или понижая увеличенные и уменьшенные интервалы дальше, мы можем получить дважды увеличенные и дважды уменьшенные интервалы.
Увеличенные и уменьшенные интервалы обращаются друг в друга, то есть ув в ум, а ум в ув.
Увеличенные и уменьшенные интервалы в тональности
В обычной тональности мы можем построить только один увеличенный интервал и один уменьшенный это всем известный тритон. Как видите по другому записать эти интервалы нельзя, что является их характерной особенностью.
Другие увеличенные и уменьшенные интервалы образуются в гармонических и мелодических видах ладов, а также при использовании альтераций.
В гармоническом мажоре 6 низкая ступень позволяет построить интервалы:
В гармоническом миноре получаем интервалы:
Для того, чтобы запомнить интервалы в тональности используем простую формулу.
Мажор переводится как большой — значит на 6 низкой ступени мажора строятся увеличенные (то есть больше чем нужно)
В миноре (переводится, как малый) на 7 повышенной строятся уменьшенные интервалы.
Интервалы ув2, ум7, ум4, ув5 появляются только в разновидностях ладов и ХАРАКТЕРИЗУЮТ их звучание, то они также называются характерными. Также они являются хроматическими, так содержат один недиатонический звук.
Разрешение характерных интервалов
При освоении гармонии и голосоведения важно знать, как разрешить интервалы.
Здесь работает очень простое правило:
Уменьшенные интервалы стремятся к уменьшению, а увеличенные к увеличению. Например, разрешение интервалов в тональности до мажор:
Получается, что наша задача просто найти ближайший устойчивый звук тональности и перейти в него.
Количественная и качественная величина интервала
Каждый интервал имеет две величины – количественную и качественную.
Количественная (или ступеневая) величина интервала – это количество охватываемых интервалом ступеней, она обозначается цифрой.
Например: интервал, содержащий три ступени – это терция и т.д.
В зависимости от количественной величины интервал получает своё название.
Качественная (или тоновая) величина интервала – это количество содержащихся в интервале тонов, она обозначается буквой.
Например: интервал, содержащий три ступени и два тона – это большая терция и т.д.
Качественная величина интервала определяет различие звучания однородных интервалов, например: малой и большой терции и т.д.
Диатонические и хроматические интервалы
Между основными ступенями звукоряда в пределах октавы образуются простые интервалы.
Они называются диатоническими или основными, так как образуются между ступенями натуральногомажора или минора.
К ним относятся все чистые, малые, большие интервалы и тритоны (увеличенная кварта и уменьшённая квинта).
Все остальные увеличенные и уменьшенные интервалы (кроме тритонов) называются хроматическими.
Интервал. Обращение интервала.
Интервалом называется расстояние между двумя звуками (cтупенями лада). Нижний звук интервала называется основанием, а верхний – вершиной.
Обращением интервала называется перенос (перемещение) нижнего звука интервала на октаву вверх или верхнего звука на октаву вниз.
В результате перемещения получается новый интервал.
Вместе с первоначальным интервалом новый интервал (его крайние звуки) составляет интервал октаву.
Первый способ – это перенос нижнего звука на октаву вверх.
Второй способ – перенос верхнего звука на октаву вниз.
При обращении интервала получается новый интервал, изменяя его вид (количественную величину и качество).
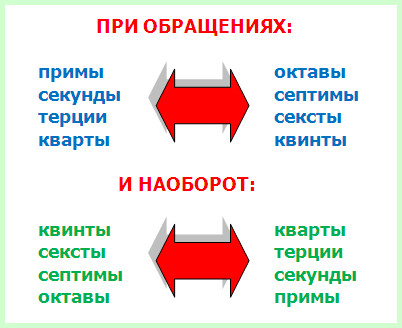
По количеству ступеней интервалы обращаются:
Прима (1) – в октаву (8),
секунда (2) – в септиму (7),
терция (3) – в сексту (6),
кварта (4) – в квинту (5). И наоборот:
Квинта (5) – в кварту (4),
секста (6) – в терцию (3),
септима (7) – в секунду (2),
октава (8) – в приму (1).
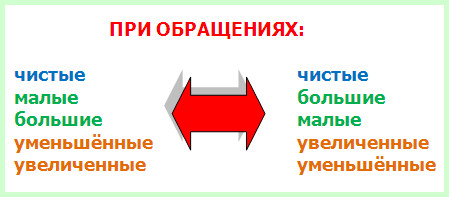
По качеству интервалы обращаются:
Малые (м) – в большие (б),
большие (б) – в малые (м),
чистые (ч) – в чистые (ч),
увеличенные (ув) – в уменьшённые (ум),
уменьшённые (ум) – в увеличенные (ув).
Аккорд. Виды трезвучий.
Аккорд – это созвучие трёх и более звуков. Из всех существующих аккордов самым распространённым является трезвучие.
Трезвучие— это аккорд, состоящий из трех звуков, расположенных по терциям (это аккорд терцового строения).
Каждый звук трезвучия имеет своё название (относительно основного тона):
Нижний звук трезвучия называется примой или основным тоном,
средний– терцией или терцовым тоном,
В зависимости от терций, входящих в состав трезвучия существует 4 вида трезвучий:
1. Мажорное трезвучие, обозначается Б5/3= б3+м3
2. Минорное трезвучие, обозначается М5/3= м3+б3
3. Увеличенное трезвучие, обозначается Ув5/3= б3+б3
4. Уменьшённое трезвучие, обозначается Ум5/3= м3+м3
Обращение интервалов или волшебство на уроках сольфеджио
Обращение интервалов – это превращение одних интервала в другие путём перестановки верхнего и нижнего звука. Как известно, нижний звук интервала называется его основанием, а верхний – вершиной.
И, если, поменять местами вершину и основание, или, другими словами, попросту перевернуть интервал вверх тормашками, то в результате получится новый интервал, который и будет являться обращением первого, исходного музыкального интервала.
Как выполняются обращения интервалов?
Сначала разберём манипуляции только с простыми интервалами. Обращение выполняется путём переноса нижнего звука, то есть основания, на чистую октаву вверх, или перемещением нижнего звука интервала, то есть вершины, на октаву вниз. Результат получится один и тот же. Перемещается только один из звуков, второй звук остаётся на своём месте, его трогать не нужно.
Например, возьмём большую терцию «до-ми» и обратим её любым способом. Сначала, основание «до» перенесём на октаву вверх, у нас получится интервал «ми-до» — малая секста. Затем попробуем поступить наоборот и перенесём вниз на октаву верхний звук «ми», в результате также получаем малую сексту «ми-до». На картинке желтым цветом выделен звук, который остаётся на месте, а сиреневым – тот, который перемещается на октаву.
Ещё пример: дан интервал «ре-ля» (это чистая квинта, так как ступеней между звуками пять, а качественная величина – три с половиной тона). Попробуем сделать обращение этого интервала. Переносим «ре» выше – получаем «ля-ре»; или переносим «ля» ниже и тоже получаем «ля-ре». В обоих случаях чистая квинта обратилась в чистую кварту.
Кстати, путём обратных действий, можно вернуться к исходным интервалам. Так, сексту «ми-до» можно обратить в терцию «до-ми», от которой мы сначала отталкивались, ну а кварту «ля-ре» легко снова превратить в квинту «ре-ля».
О чём это говорит? Это говорит о том, что между разными интервалами есть какая-то связь, и о том, что существуют пары взаимно обращаемых интервалов. Эти интересные наблюдения легли в основу законов интервальных обращений.
Законы обращения интервалов
Мы знаем, что у любого интервала есть два измерения: количественная и качественная величина. Первая выражается в том, сколько ступеней охватывает тот или иной интервал, обозначается числом, и от неё зависит название интервала (прима, секунда, терция и другие). Вторая указывает на то, сколько в интервале тонов или полутонов. И, благодаря ей, у интервалов появляются дополнительные уточняющие названия из слов «чистый», «малый», «большой», «увеличенный» или «уменьшённый». Следует отметить, что оба параметра интервала меняются при обращении – и ступеневый показатель, и тоновый.
Законов-правил всего два.
Правило 1. Чистые интервалы при обращении остаются чистыми, малые превращаются в большие, а большие, наоборот, в малые, уменьшённые делаются увеличенными, ну а увеличенные интервалы, в свою очередь, уменьшёнными.
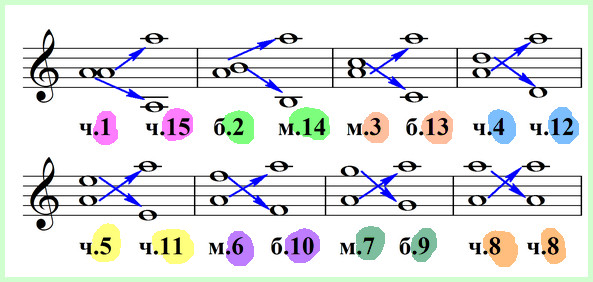
Правило 2. Примы обращаются в октавы, а октавы – в примы; секунды переходят в септимы, а септимы – в секунды; терции становятся секстами, а сексты – терциями, кварты перевоплощаются в квинты, а квинты, соответственно, в кварты.
Сумма обозначений взаимообращающихся простых интервалов равна девяти. Например, прима обозначается числом 1, октава – числом 8. 1+8=9. Секунда – 2, септима – 7, 2+7=9. Терции – 3, сексты – 6, 3+6=9. Кварты – 4, квинты – 5, вместе снова получается 9. И, если вдруг вы забыли, кто куда обращается, то просто из девятки вычитайте числовое обозначение данного вам интервала.
Давайте посмотрим действие этих законов на практике. Даны несколько интервалов: чистая прима от ре, малая терция от ми, большая секунда от до-диеза, уменьшённая септима от фа-диеза, увеличенная кварта от ре. Обратим их и выявим изменения.
Итак, после обращения чистая прима от ре превратилась в чистую октаву: тем самым находят подтверждения два момента: во-первых, чистые интервалы и после обращения остаются чистыми, а, во-вторых, прима стала октавой. Далее, малая терция «ми-соль» после обращения явилась как большая секста «соль-ми», что снова подтверждает уже сформулированные нами законы: малое выросло в большое, терция стала секстой. Следующий пример: большая секунда «до-диез и ре-диез» превратилась в малую септиму из тех же звуков (малое – в большое, секунда – в септиму). Аналогично и в других случаях: уменьшённое становится увеличенным и наоборот.
Проверь себя!
Предлагаем немного потренироваться для лучшего закрепления темы.
ЗАДАНИЕ: Дан ряд интервалов, нужно определить, что это за интервалы, затем мысленно (или письменно, если трудно так сразу) обратить их и сказать, во что они превратятся после обращения.
1) даны интервалы: м.2; ч.4; м.6; б.7; ч.8;
2) после обращения из м.2 получаем б.7; из ч.4 – ч.5; из м.6 – б.3; из б.7 – м.2; из ч.8 – ч.1.
Фокусы с составными интервалами
Составные интервалы тоже могут участвовать в обращении. Напомним, что составными называются интервалы, которые шире октавы, то есть ноны, децимы, ундецимы и другие.
Чтобы получить при обращении из простого интервала составной, нужно переместить одновременно и вершину, и основание. Причём, основание – на октаву вверх, а вершину – на октаву вниз.
Например, возьмём большую терцию «до-ми», переместим основание «до» на октаву выше, а вершину «ми», соответственно, на октаву ниже. В результате такого двойного перемещения у нас получился широкий интервал «ми-до», секста через октаву, или, если быть точнее, малая терцдецима.
Подобным же образом, и другие простые интервалы можно превратить в составные и, наоборот, из составного интервала можно получить простой, если вершину его на октаву опустить, а основание поднять.
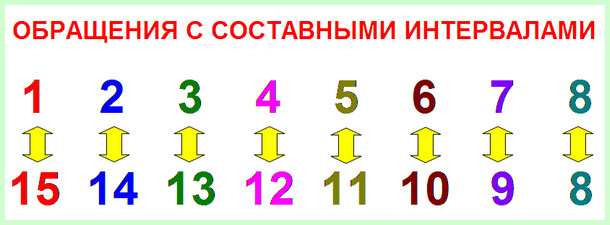
Какие будут соблюдаться закономерности? Сумма обозначений двух взаимообращаемых интервалов будет равна шестнадцати. Так:
Применение обращений интервалов
Не стоит думать, что обращения интервалов, так подробно изучаемые в курсе школьного сольфеджио, не имеют никакого практического применения. Напротив, это очень важная и нужная штука.
Практическая область применений обращений связана не только с пониманием того, как возникли некоторые интервалы (да-да, исторически некоторые интервалы были обнаружены путём обращения). Если брать теоретическую область, то обращения очень помогают, например, в запоминании тритонов или характерных интервалов, изучаемых в старших классах и в колледжах, в понимании устройства некоторых аккордов.
Если брать область творческую, то обращения широко применяются при сочинении музыки, причём иногда мы даже их не замечаем. Послушайте, например, кусочек красивой мелодии в романтическом духе, он весь построен на восходящих интонациях терций и секст.
Вы, кстати, тоже легко можете попробовать сочинить нечто подобное. Даже, если взять те же терции и сексты, только в нисходящей интонации:
P.S. Дорогие друзья! На этой ноте мы завершаем сегодняшний выпуск. Если у вас остались ещё вопросы об обращениях интервалов, то, пожалуйста, задайте их в комментариях к этой статье.
P.P.S. Для окончательного усвоения данной темы предлагаем вам посмотреть забавное видео от замечательного учителя сольфеджио наших дней Анны Наумовой.