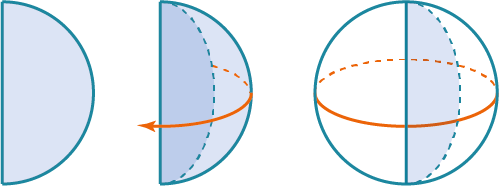
в результате вращения какой фигуры получается сфера

Тела вращения и их сечения

Телом вращения называется тело, образованное в результате вращения какой-либо линии вокруг прямой.

Примеры тел вращения.

Шар − образован полукругом, вращающимся вокруг диаметра разреза.

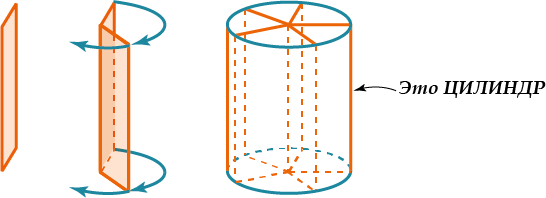
Цилиндр − образован прямоугольником, вращающимся вокруг одной из сторон.

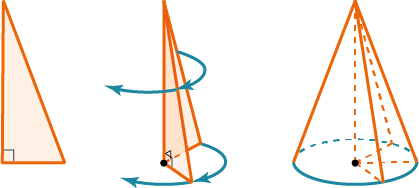
Конус − образован прямоугольным треугольником, вращающимся вокруг одного из катетов.

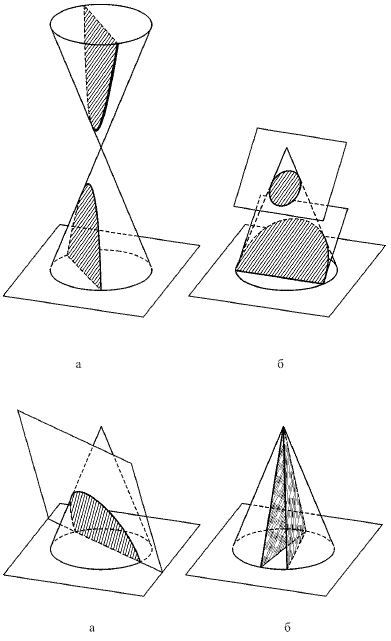
При пересечении тела вращения плоскостью получается плоская фигура, ограниченная в большинстве случаев кривой линией. В частных случаях фигурой сечения может быть прямоугольник (для цилиндра) и треугольник (для конуса).

Осевым сечением цилиндра называется сечение плоскостью, проходящей через ось цилиндра. Осевое сечение цилиндра – прямоугольник, две стороны которого – образующие цилиндра, а две другие стороны – диаметры оснований цилиндра.

Секущая плоскость, перпендикулярная оси цилиндра, пересекает его по кругу.

Если плоскость проходит через высоту конуса FO, то сечение конуса этой плоскостью называют осевым и оно представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса, а боковыми сторонами – образующие конуса.

Сечение поверхности цилиндра

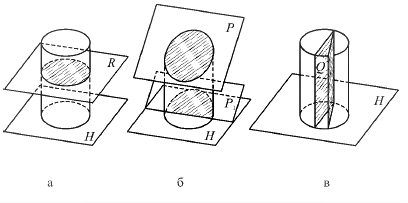
Бывают следующие случаи сечения поверхности прямого кругового цилиндра плоскостью:

1) окружность, если секущая плоскость Р перпендикулярна оси цилиндра, причем она параллельна основанию цилиндра;

2) эллипс, если секущая плоскость Р не перпендикулярна и не параллельна оси цилиндра;

3) пара прямых, если секущая плоскость Q содержит ось цилиндра или параллельна ей.

Рис. 104. Возможные случаи сечения поверхности цилиндра плоскостью: а – окружность; б – эллипс; в – пара прямых

Сечение поверхности конуса

В общем случае круговая коническая поверхность включает в себя две совершенно одинаковые полости, которые имеют общую вершину. Образующие одной полости представляют собой продолжение образующих другой полости.

Бывают различные случаи сечения поверхности кругового конуса плоскостью.

1. Эллипс, если секущая плоскость не параллельна ни одной образующей (рис. 107 б). Здесь секущая плоскость пересекает поверхность только одной полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса меньше угла, который образующая конуса составляет с основанием конуса. Здесь угол является углом, который образующая составляет с основанием.

Рис. 107. Различные случаи сечения поверхности кругового конуса плоскостью: а – гипербола; б – эллипс; в – парабола; г – пара прямых

2. Парабола, если секущая плоскость параллельна только одной образующей (рис. 107 в).

3. Гипербола, если секущая плоскость параллельна двум образующим (рис. 107 а). При этом секущая плоскость пересекает обе полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса больше угла.

4. Пара прямых, если секущая плоскость проходит через вершину конуса и угол ее наклона к основанию конуса больше угла. Этот случай иногда рассматривают как частный случай гиперболы.

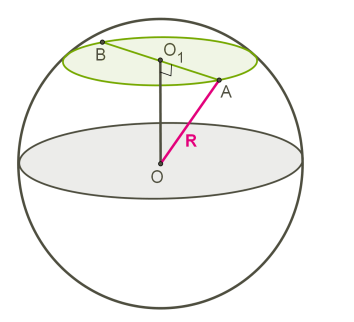
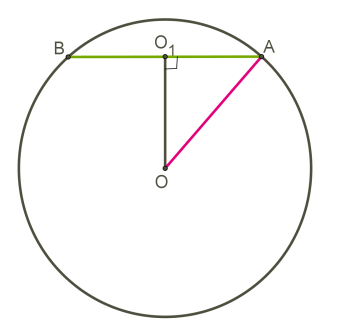
Сечение шара

Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара). Основание перпендикуляра, проведенного из центра шара к пересекаемой плоскости, есть центр круга, полученного в сечении.

При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.

Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.

Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).

Источник

Тела и поверхности вращения. Шар. Цилиндр. Конус

Тела и поверхности вращения.

Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.

Подробная теория с наглядными иллюстрациями и основные формулы.

Читай эту статью, здесь все это есть.

Всего за 15 минут ты полностью во всём разберешься!

Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.

Вот самый простой пример: цилиндр.

Берем прямоугольник и начинаем вращать его вокруг одной из сторон.

А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.

Что получится? Бублик. А по-научному – ТОР.

Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.

Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.

Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.

Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)

Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.

Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:

«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.

Ну, в общем, шар он и есть шар.

Названия, которые ты должен знать:

Незнакомое тебе, наверное, только одно.

Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.

Площадь поверхности сферы

Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.

Объем шара

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.

Если ты знаком с производной, то можешь заметить это:

И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!

Цилиндр

Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.

Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:

Основания у цилиндра – это круги

Еще у цилиндра есть так называемая развертка.

Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.

Что получится? Представь себе, прямоугольник.

Развертка цилиндра – прямоугольник.

Площадь боковой поверхности цилиндра

\( H\) – высота, она же образующая.

Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник \( 2\pi R\cdot H\).

Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра.

Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому

Площадь полной поверхности цилиндра

Прибавляем теперь площадь двух кругов – оснований и получаем:

Можно вынести (хотя и не обязательно) \( 2\pi R\):

Но эту формулу неудобно запоминать!

Объем цилиндра

\( R\) – радиус основания \( H\) – высота

\( V=<_<основания>>\cdot H\), только у призмы и параллелепипеда \( <_<основания>>\) — это площадь многоугольника, а у цилиндра \( <_<основания>>\) — это площадь круга.

Конус

Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.

И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».

Названия, относящиеся к конусу:

Что тут нужно твердо помнить?

Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.

У конуса тоже есть развертка.

Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?

Представь себе сектор круга. Пусть длина образующей равна \( l\).

Развертка конуса – сектор круга радиуса \( l\)

Площадь поверхности конуса

Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.

По формуле площади сектора \( <_<бок.>>=<^<2>>\cdot \frac<\alpha ><2>\) Где \( \alpha \) – угол при вершине в радианах.

И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.

Но если все же даны только образующая и радиус основания, как быть?

Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна \( 2\pi R\).

С другой стороны, длина этой же дуги равна \( \alpha \cdot l\), так как это дуга окружности радиуса \( l\). Поэтому

\( R\) — радиус окружности основания,

\( l\) — длина образующей

Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:

Можно вынести \( \pi R\):

Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.

Объём конуса

\( R\) – радиус основания \(

Это так же, как у пирамиды

\( <_<осн. >>\) — это не площадь многоугольника, а площадь круга.

А вот откуда взялась \( \frac<1><3>\)?, по-прежнему остается загадкой, потому что эта \( \frac<1><3>\) получена в результате довольно хитрых рассуждений умных математиков.

А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта \( \frac<1><3>\) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.

Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

К ЕГЭ можно подготовиться абсолютно бесплатно. У нас на сайте полно качественных материалов. Но вы должны знать что вы делаете.

Если у вас с этим сложности, приходите к нам.

И если вам нужен действительно высокий балл, приходите на наши курсы:

Мы качественно готовим к ЕГЭ даже тех, у кого «нет способностей».

Твой ход!

Ну как тебе? Понравилось?

Держу пари, даже если ты первый раз слышишь о телах вращения, ты сейчас чувствуешь себя намного увереннее в этой теме!

А теперь мы хотим услышать тебя. Нам очень интересно твое мнение об этой статье!

Напиши его в комментариях ниже!

Помогла ли тебе эта статья? Достаточна ли она подробна?

Остались вопросы? Задай их!

Мы ответим. Мы читаем все.

Добавить комментарий Отменить ответ

Один комментарий

Некоторые комментарии прошлых лет к этой статье:

Мария
07 февраля 2018
Очень понятно, доступно

Александр (админ)
07 февраля 2018
Мария, мы рады! Заходи к нам и делись с друзьями!

Евгений
05 марта 2018
Сайт замечательный! Совокупность лёгкого и понятного для прочтения текста и самих рисунков отличная.

Александр (админ)
05 марта 2018
Спасибо, Евгений! Заходи… )

Левон
09 мая 2018
Потрясающе! Я в восторге. Всё так хорошо расписано и показано, даже предлагают как можно легче формулами воспользоваться. Продолжайте в том же духе!

Александр (админ)
09 мая 2018
Спасибо большое, Левон!

Дилдора
18 мая 2018
Да, отлично! Мне тоже понравился. А как можно скачать, чтобы воспользоваться.

Александр (админ)
18 мая 2018
Дилдора, привет! К сожалению пока скачать никак нельзя ((( Только если по кускам делать скриншоты и потом распечатать. Руки не доходят сделать.

Таня
18 июня 2018
Молодцы, ребята. Это доступно, лаконично, толково. Успехов Вам и нам.

Максим
23 мая 2019
Прекрасный сайт. Дела. сейчас реферат по этой теме, обычно приходится сокращать, а здесь наоборот лить воду) Купил бы что-нибудь не для того, чтобы читать, а чтобы этот сайт жил, но, к сожалению, сам студент и деняк нема(

Александр (админ)
23 мая 2019
Ничего, Максим, студенты становятся профи и начинают зарабатывать. Все будет тип-топ! За добрые слова спасибо!

Геннадий
31 июля 2019
А если образующая колонны — дуга вытянутого эллипса, то какова боковая поверхность этой колонны?

Алексей Шевчук
01 августа 2019
Геннадий, здесь не обойтись без интеграла. Нужно знать зависимость радиуса колонны от высоты (например, можно вывести из уравнения эллипса).

Геннадий
09 августа 2019
Алексей! В одной из традиций такие образующие могли строить по контрольным точкам. Эллипс с полуосями 1040 и 65 (соотношение 16 к 1) модулей являет 36 точек с целочисленными координатами. Высота колонны — 256 модулей, верхний радиус — 14 модулей, а нижний — 16 модулей. Ось колонны паралельна вертикальной оси разметочного эллипса. Растояние между этими осями — 49 модулей. Основание колонны проецируем на малую ось данного эллипса.

Алексей Шевчук
13 августа 2019
Геннадий, ни эллипсы, ни интегрирование (на нужном для этой задачи уровне) в школьной программе не проходятся. Вкратце Ваша задача решается так: 1) Сначала необходимо составить уравнение эллипса. Например, в виде (x-x0)^2/a^2+(y-y0)^2/b^2 = 1 (рекомендую взять x0=49 и y0=0). 2) Пользуясь этим уравнением, можно вывести зависимость радиуса колонны от высоты (при х0=49 и у0=0 нужно будет просто выразить x из уравнения). 3) Нужно вычислить, на каких высотах y1 и y2 радиусы равны 14 и 16 (таких пар будет несколько, зависит от того, выпуклая колонна или вогнутая) — в Вашем случае всё просто, это 256 и 0. 4) наконец, нужно взять определённый интеграл по dy с пределами y1 и y2 от функции 2*pi*x (длины окружности на каждой высоте). Чтобы упростить вычисления, рекомендую пользоваться программами типа wolfram alpha.

Геннадий
22 августа 2019
Здравствуйте, Алексей! Спасибо за ответ. Колонна, скажем так, выпуклая. Ее нижний радиус — наибольший, а верхний — наименьший. Локальных перепадов типа «+» — «-» — «+» нет. Мой вопрос (к сожалению) был не очень корректно сформулирован. Интересует не столь площадь боковой поверхности, сколько название этой поверхности (нечто вроде «шарового пояса»). Например «пояс эллиптического тора»?…

Алексей Шевчук
25 августа 2019
Пояс закрытого эллиптического тора вполне подойдёт. Правда, не уверен, что Вы найдёте готовые формулы вычисления для подобных фигур

Геннадий
28 августа 2019
Спасибо. Это был вопрос корректной формулировки. Интересно, что когда полуоси исходного эллипса 65 и 1040, то его «тело» разбивается на 36 простых (последовательных) дуг с целочисленными координатами.

KIZARU
24 октября 2019
Не лезьте в хип-хоп

Александр (админ)
24 октября 2019
Хорошо. Не будем.

Источник

Конспекты по математике на тему «Тела вращения. Объемы тел вращения»

Ищем педагогов в команду «Инфоурок»

Конспекты занятий по математике для студентов первого курса теме «Тела вращения. Объемы тел вращения».

Тела вращения — объёмные тела, полученные при вращении плоской фигуры вокруг своей оси или стороны.

Примеры тел вращения: цилиндр, конус, шар, сфера.

Цили́ндр (от греч. kýlindros, валик, каток) — геометрическое тело, образованное вращением прямоугольника вокруг одной из сторон.

Примеры тел, имеющих цилиндрическую форму: часть водопроводной трубы, консервная банка.

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между его основаниями.

Осью цилиндра называется прямая, проходящая через центр оснований, параллельно образующим.

Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.

Поверхность цилиндра состоит из оснований и боковой поверхности.

Боковая поверхность составлена из образующих.

Основания цилиндра равны и параллельны.

Образующие цилиндра равны и параллельны.

Ко́нус — тело вращения, образованное вращением прямоугольного треугольника, вокруг одного из его катетов.

Шар — тело вращения, полученное вращением полукруга около его неподвижного диаметра.

Примеры тел, имеющих форму шара или сферы: мыльный пузырь, земля, футбольный и теннисный мячи.

Сфера это поверхность шара .

Концы любого диаметра называются диаметрально противоположными точками шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

1. Уравнение шара с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 ≤ R 2

2. Уравнение шара с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

Формулы объема цилиндра, конуса и шара.

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

3. Объем усеченного конуса.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Источник

Фигуры вращения

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Описание слайда:

ПОВОРОТ
Пусть теперь в пространстве задана прямая a и точка A, не принадлежащая этой прямой. Через точку A проведем плоскость α, перпендикулярную прямой a, и точку пересечения a и  обозначим O. Говорят, что точка A’ пространства получается из точки A поворотом вокруг прямой a на угол φ, если в плоскости α точка A’ получается из точки A поворотом вокруг центра O на угол φ.
Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол φ называется поворотом, или вращением. Прямая a при этом называется осью вращения.

Описание слайда:

ФИГУРЫ ВРАЩЕНИЯ
Говорят,что фигура Ф в пространстве получена вращением фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.
При вращении точки A вокруг прямой a получается окружность.
Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.

Описание слайда:

ФИГУРЫ ВРАЩЕНИЯ
Цилиндр получается вращением прямоугольника вокруг одной из его сторон.
Конус получается вращением прямоугольного треугольника вокруг одного из его катетов.
Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу.

Описание слайда:

ФИГУРЫ ВРАЩЕНИЯ
Если окружность вращать вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек, то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик.
При вращении эллипса вокруг его оси получается поверхность, называемая эллипсоидом вращения.

Описание слайда:

ФИГУРЫ ВРАЩЕНИЯ
При вращении параболы вокруг ее оси получается поверхность, называемая параболоидом вращения.
При вращении гиперболы вокруг ее оси получается поверхность, называемая гиперболоидом вращения.

Описание слайда:

ФИГУРЫ ВРАЩЕНИЯ
Если прямая параллельна оси, то при вращении получается фигура, называемая цилиндрической поверхностью. Если прямая пересекает ось, то при вращении получается фигура, называемая конической поверхностью.

Описание слайда:

ГИПЕРБОЛОИД ВРАЩЕНИЯ
Теорема. При вращении прямой, скрещивающейся с осью вращения, получается гиперболоид вращения.

Описание слайда:

ВРАЩЕНИЕ КУБА 1
При вращении куба вокруг диагонали получается фигура, поверхность которой состоит из боковых поверхностей двух конусов и поверхности гиперболоида вращения.

Описание слайда:

ВРАЩЕНИЕ КУБА 2
При вращении куба вокруг прямой, соединяющей середины двух противоположных ребер, получается фигура, поверхность которой состоит из двух кругов и двух поверхностей гиперболоидов вращения.

Описание слайда:

Упражнение 1
Какая фигура получается при вращении отрезка OA вокруг прямой, проходящей через точку O и перпендикулярной OA?
Ответ: Круг.

Описание слайда:

Упражнение 2
Назовите прямые, при вращении вокруг которых данного прямоугольника получается цилиндр.
Ответ: Прямые, пересекающие прямоугольник по отрезку, параллельному его стороне.

Описание слайда:

Упражнение 3
Какая фигура получается при вращении равнобедренного треугольника вокруг прямой, содержащей высоту, опущенной на основание этого треугольника?
Ответ: Конус.

Описание слайда:

Упражнение 4
Какая фигура получается при вращении полукруга вокруг прямой, содержащей диаметр?
Ответ: Круг.

Описание слайда:

Упражнение 5
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей его катет?
Ответ: Конус.

Описание слайда:

Упражнение 6
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, и проходящей через вершину острого угла перпендикулярно катету?
Ответ: Цилиндр, из которого вырезан конус.

Описание слайда:

Упражнение 7
Какая фигура получается вращением равнобедренного прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, перпендикулярной гипотенузе и проходящей через вершину острого угла.
Ответ: Усеченный конус, из которого вырезан конус.

Описание слайда:

Упражнение 8
Какая фигура получается вращением остроугольного треугольника вокруг прямой, содержащей его сторону?
Ответ: Фигура, состоящая из двух конусов с общим основанием.

Описание слайда:

Упражнение 9
Ответ: Усечённый конус с вырезанным внутри конусом.
Какая фигура получается вращением остроугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через его вершину перпендикулярно стороне?

Описание слайда:

Упражнение 10
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, содержащей его сторону, прилегающую к тупому углу?
Ответ: Фигура, полученная из конуса, вырезанием из него другого конуса.

Описание слайда:

Упражнение 11
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через вершину тупого угла параллельно противолежащей стороне?
Ответ: Цилиндр с вырезанными внутри двумя конусами, имеющими общую вершину.

Описание слайда:

Упражнение 12
Какая фигура получается вращением прямоугольника вокруг прямой, лежащей в плоскости этого прямоугольника, параллельной его стороне, и не имеющей с ним общих точек?
Ответ: Фигура, полученная из цилиндра, вырезанием из него другого цилиндра.

Описание слайда:

Упражнение 13
Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее её основание?
Ответ: Цилинд с вырезанными внутри двумя конусами.

Описание слайда:

Упражнение 14
Какая фигура получается вращением трапеции вокруг прямой, содержащей большее её основание?
Ответ: Цилиндр, на основания которого поставлены конусы.

Описание слайда:

Упражнение 15
Какая фигура получается при вращении куба вокруг прямой, соединяющей центры противоположных граней.
Ответ: Цилиндр.

Описание слайда:

Упражнение 16
Какая фигура получится при вращении правильной n-угольной призмы вокруг прямой, проходящей через центры ее оснований?
Ответ: Цилиндр.

Описание слайда:

Упражнение 17
Какая фигура получается при вращении правильной n-угольной пирамиды вокруг прямой, содержащей ее высоту?
Ответ: Конус.

Описание слайда:

Упражнение 18
Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей середины скрещивающихся ребер?
Ответ: Фигура, ограниченная двумя кругами и гиперболоидом вращения.

Описание слайда:

Упражнение 19
Какая фигура получается при вращении октаэдра вокруг прямой, проходящей через противоположные вершины?
Ответ: Фигура, состоящая из двух конусов с общим основанием.

Описание слайда:

Упражнение 20
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Показательной функции.

Описание слайда:

Упражнение 21
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Синусоиды.

Описание слайда:

Упражнение 22
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ:

Описание слайда:

Упражнение 23
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ:

Описание слайда:

Упражнение 24
Тетраэдр повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является объединением и пересечением исходного тетраэдра и повернутого?
Ответ: Звезда Кеплера, октаэдр.

Описание слайда:

Упражнение 25
Куб повернут вокруг прямой, соединяющей центры противоположных граней, на угол 45о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Правильная 8-я призма.

Описание слайда:

Упражнение 26
Куб повернут вокруг диагонали на угол 60о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Правильная 6-я бипирамида.

Описание слайда:

Упражнение 27
Куб повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Две правильные 4-е пирамиды, поставленные на основания правильной 4-ой призмы.

Описание слайда:

Упражнение 28
Октаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол 45о. Какая фигура является общей частью исходного октаэдра и повернутого?
Ответ: Правильная 8-я бипирамида.

Описание слайда:

Упражнение 29
Октаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на угол 60о. Какая фигура является общей частью исходного октаэдра и повернутого?
Ответ: Правильная усеченная 6-я бипирамида.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Охрана труда

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

Начальные геометрические сведения 7 класс

Решение задач на применение аксиом стереометрии и их следствий

Столбчатые диаграммы 6 класс

Урок геометрии в 8а классе

Свойства производной. Построение графиков функций

Построение объёма

Практическая геометрия у разных народов мира

Задачи на построение сечений

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5246732 материала.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Около половины детей болеют коронавирусом в бессимптомной форме

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

Минтруд предложил проект по реабилитации детей-инвалидов

Время чтения: 1 минута

Средняя зарплата учителей в Москве достигла 122 тыс. рублей

Время чтения: 1 минута

Минпросвещения объявило конкурс «Учитель-международник»

Время чтения: 1 минута

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник