в результате вращения какой фигуры получается усеченный конус

Что такое усеченный конус: определение, основные элементы

В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение усеченного конуса

Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.

Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.

Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.

На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O₁O₂.

Основные элементы усеченного конуса

Развёртка боковой поверхности усеченного конуса выглядит следующим образом:

Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).

Источник

Предмет: Математика (2 семестр) Проверочная работа в тестовой форме.

Предмет: Математика (2 семестр)

Проверочная работа в тестовой форме. Вариант № 1

Отрезок, соединяющий вершину правильной пирамиды с серединой одной из сторон основания, называется:

А). диагональю; Б). апофемой; В). высотой; Г). радиусом.

В результате вращения какой фигуры получается усеченный конус?

А). прямоугольника; Б). шара; В). треугольника; Г). трапеции.

Выберите правильное утверждение, у тетраэдра

А). 6 вершин; Б). 8 ребер; В). 4 грани; Г). 3 стороны.

Если две параллельные плоскости пересечены третьей, то линии их пересечения

А). равны; Б). параллельны;

Если две прямые лежат в одной плоскости и не имеют общих точек, то они называются

А). скрещивающимися; Б). параллельными ;

В). пересекающимися; Г). перпендикулярными.

Какая фигура является осевым сечением шара?

А). прямоугольник; Б).круг; В).окружность; Г). трапеция.

Областью определения функции

является:

А). (0; Б).(3; 2); В). (-; Г). (10;0)

Производная любой постоянной равна:

А). 0; Б). 2; В). ; Г). 10

Если диагональ куба равна 3 ед., то ребро куба равно:

А). 2; Б). 9 ; В). 1; Г).

В правильной усеченной пирамиде периметры верхнего и нижнего оснований соответственно равны 4 см и 10 см, а апофема равна 20 см. Определить площадь боковой поверхности.

Определите площадь осевого сечения цилиндра, если оно имеет форму квадрата, а радиус основания цилиндра равен 3 см.

А). 9см2; Б). 18см2; В). 36см2

Чему равен объем конуса, если его высота равна радиусу основания и равна см?

А). ; Б). ; В)1; Г). р.

Определите радиус сферы, если ее площадь равна 400р см2.

А). ; Б). 50; В).100

Чему равна площадь боковой поверхности прямого параллелепипеда, если каждое его ребро равно 2 см.

А). 8см2; Б). 16см2; В). 24см2 2

Найти предел последовательности:

А). 3; Б). 2; В). ; Г). 1;

Найти предел функции:

Найти производную функции:

А).; Б). 2; В). ; Г). 5

Найти:

А). Б). 0; В). ; Г). 3

Вычислить:

Найти площадь фигуры, ограниченной линиями:

А). 2ед2; Б). 5ед2; В). ед2

Предмет: Математика (2 семестр)

Проверочная работа в тестовой форме. Вариант № 2

Производная функции равна:

А). 3; Б). 0; В). ; Г). 10

Если две прямые имеют одну общую точку, то они называются

А). параллельными; Б).скрещивающимися ; В).пересекающимися; Г).перпендикулярными.

Отрезок, соединяющий вершину правильной пирамиды с центром основания, называется:

А). апофемой ; Б). радиусом Г). диагональю; В). высотой.

Многогранник, все грани которого являются квадратами, называется

А). пирамидой; Б). шаром;

Если две прямые параллельны третьей, то они между собой

А). параллельны ; Б). равны;

В). перпендикулярны; Г). скрещиваются.

Выберите правильное утверждение, у октаэдра

А). 6 вершин ; Б). 8 ребер; В). 4 грани; Г).3 стороны.

В результате вращения какой фигуры получается конус?

Б). треугольника; В). трапеции; Г). шара.

Какая фигура является осевым сечением конуса?

А). прямоугольник; Б).треугольник; В).трапеция; Г). круг.

Если диагональ куба равна 6 ед, то ребро куба равно:

А). ; Б).1; В). 3;

Г). 2 ед.

В правильной усеченной пирамиде периметры верхнего и нижнего оснований соответственно равны 3 см и 6 см, а апофема равна 10 см. Определить площадь боковой поверхности.

А). 100 см2; Б). 45 см2;

В). 150 см2; Г). 15 см2

Определите площадь осевого сечения цилиндра, если оно имеет форму квадрата, а радиус основания цилиндра равен 5 см.

Чему равен объем конуса, если его высота равна радиусу основания и равна 3 см?

А). 9р см3; Б). 10р см3;

В). 15р см3. В). 5р см3.

Определите радиус сферы, если ее площадь равна 800р см2.

А). 10 ; Б). ; В). 5 . Г).1.

Чему равна площадь боковой поверхности прямого параллелепипеда, если каждое его ребро равно 3 см.

Найти предел последовательности:

А). 3; Б). 2; В). ; Г). 1;

Найти предел функции:

Найти производную функции:

А).4; Б). 2; В). ; Г). 5

Найти:

А). Б). 0; В). ; Г).

Вычислить:

Найти площадь фигуры, ограниченной линиями:

А). 2ед2; Б). 5ед2; В). 9ед2

Предмет: Математика (2 семестр)

Проверочная работа в тестовой форме. Вариант № 3

Если две прямые не лежат в одной плоскости, то они называются

В результате вращения какой фигуры получается конус?

А). прямоугольника; Б). трапеции ; В). треугольника; Г). круга.

Отрезки параллельных прямых, заключенные между параллельными плоскостями

А). равны; Б). не лежат в одной плоскости; В). пропорциональны.

Выберите правильное утверждение: у тетраэдра

А). 4 грани; Б).6 вершин;

В). 8 ребер; Г). 3 стороны.

Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:

А). высотой пирамиды;

Б). апофемой; В). диагональю.

Производная равна:

А). 3; Б). 0; В). ; Г). 1

Областью определения функции является:

А). (0; Б). (3; 2); В). (-;

Какая фигура является осевым сечением цилиндра?

А). прямоугольник; Б).круг; В).окружность; Г). трапеция.

Радиус основания цилиндра 3 см. Чему равна площадь осевого сечения цилиндра, если оно имеет форму квадрата?

А). 36 см2 Б). 18 см2 В). 9см2

Чему равен объем конуса, если его высота равна радиусу основания и равна см?

А). см3; Б). р см3; В). р см3;

Чему равен объем шара, если его радиус равен см?

А). см3; Б). 4рсм3; В).2см3;

Чему равна площадь полной поверхности тетраэдра, если все его ребра равны по 2 см?

А). 4 см2; Б). 8 см2; В). 8 см2;

Если диагональ куба равна 3ед, то ребро куба равно:

А). ед; Б). 2 ед;

Определите радиус сферы, если ее площадь равна 100р см2.

А). 1см ; Б). ;

В). . Г)..

Найти предел последовательности:

А). 3; Б). 2; В). ; Г). 1;

Найти предел функции:

Найти производную функции:

А).5; Б). 2; В). ; Г). 5

Найти:

А). Б). 0; В). ;

Г). .

Вычислить:

Найти площадь фигуры, ограниченной линиями:

А). 2ед2; Б). 5ед2; В). 9ед2

Источник

Рассмотрение свойств объемных фигур является одной из приоритетных задач геометрии. Важными характеристиками всех пространственных фигур являются объем и площадь поверхности. В статье раскрывается вопрос о том, что это — усеченный конус, и приводятся формулы для определения площади его поверхности и объема.

Фигура конус

Вам будет интересно: «Земляк» – это соотечественник и поддержка на чужбине

Расстояние между вершиной фигуры и основанием называется высотой. Если соответствующий перпендикуляр пересекает основание в геометрическом центре, то фигуру называют прямой.

Вам будет интересно: Полиакриловая кислота: способ получения, свойства, структура и практическое применение

Дальше в статье покажем, как, используя прямой круглый конус, получить усеченную фигуру.

Усеченный конус и способы его получения

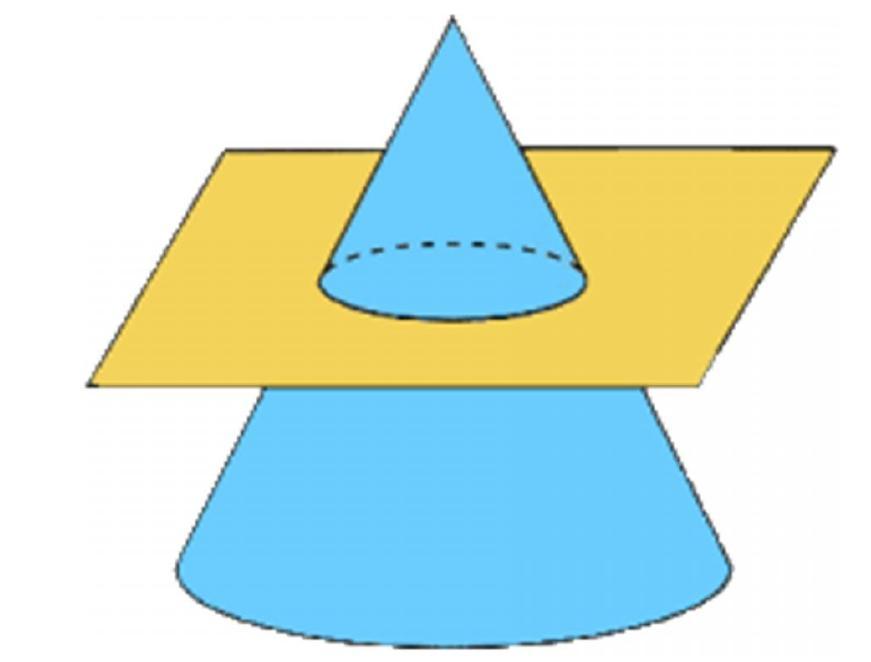
Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.

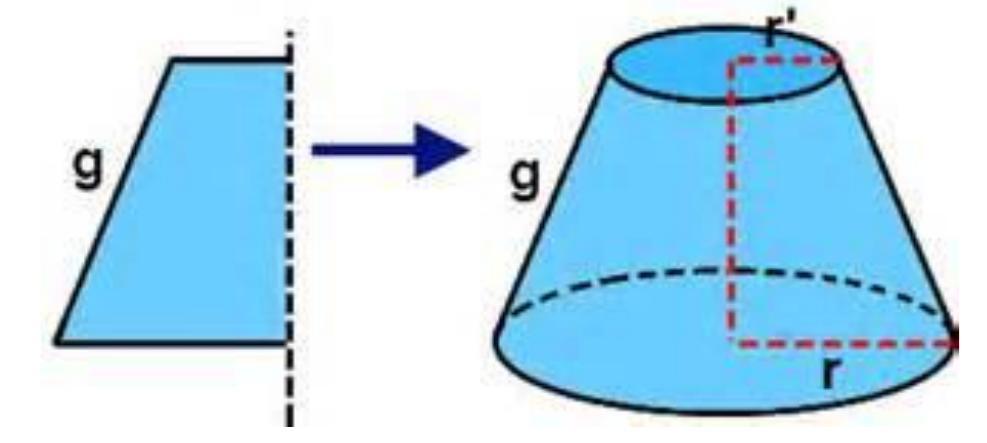
Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.

Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r’.

Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.

Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.

Элементы фигуры и ее линейные характеристики

Все четыре параметра используются для определения площади поверхности и объема.

Поверхность усеченного конуса

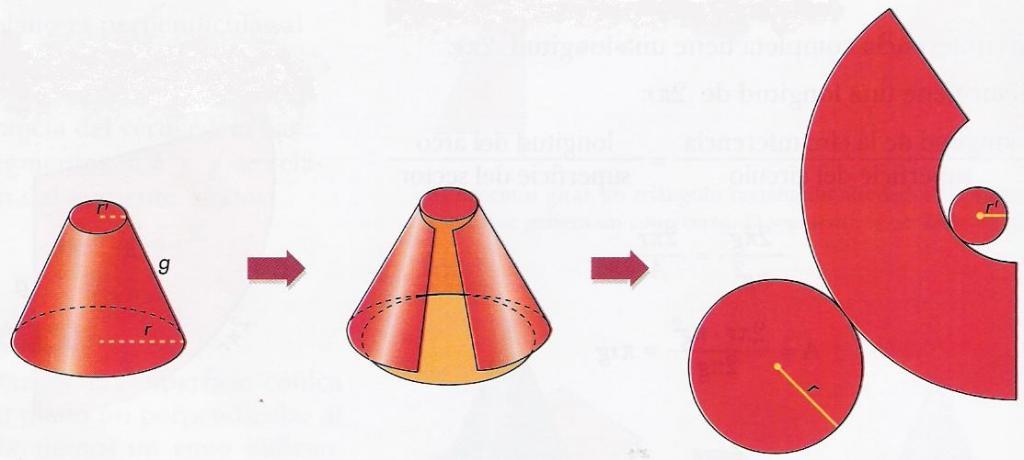
Как отмечалось, состоит поверхность фигуры из трех частей. Если отрезать каждое из оснований от фигуры, а затем вдоль образующей разрезать и развернуть боковую поверхность, то мы получим развертку усеченного конуса. Рисунок ниже показывает, как она выглядит.

Площади оснований усеченного конуса находятся по простой формуле для соответствующей величины круга:

С площадью боковой поверхности дело обстоит несколько сложнее. Можно заметить, что она представляет собой сектор круга, некоего радиуса G, у которого вырезали центральную часть радиусом G-g. Если это учесть, то можно получить формулу для площади боковой поверхности Sb. Здесь ограничимся лишь приведением конечного выражения:

Это выражение можно записать через радиусы и высоту h, однако тогда оно будет иметь несколько громоздкий вид.

Складывая записанные выражения, получаем формулу для определения площади S всей поверхности усеченного конуса:

S = So1 + So2 + Sb = pi × r12 + pi × r22 + pi × (r1 + r2) × g =

= pi × (r12 + r22 + (r1 + r2) × g)

Объем фигуры

Как и любая фигура в пространстве, усеченный конус тоже обладает некоторым объемом. Этот объем ограничен двумя основаниями и боковой поверхностью. Здесь не будем приводить подробный вывод соответствующей формулы для V. Запишем, как и в случае с площадью поверхности, лишь конечный результат:

V = h × pi / 3 × (r12 + r22 + r1 × r2)

Эта формула, в отличие от выражения для площади S, в качестве параметров содержит радиусы усеченного конуса и его высоту.

Далее в статье покажем, как следует использовать приведенные формулы для решения конкретной геометрической задачи.

Задача на определение площади и объема усеченного конуса

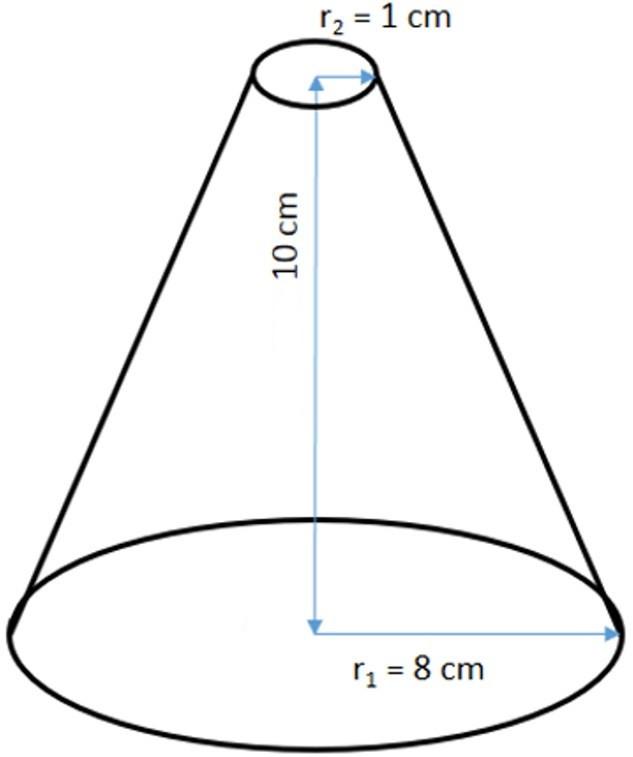
Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.

Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:

V = h × pi / 3 × (r12 + r22 + r1 × r2) =

= 10 × 3,14 / 3 × (82 + 12 + 8 × 1) ≈ 764,07 см3

Найденное значение соответствует 0,76 литра.

Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:

Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:

S = pi × (r12 + r22 + (r1 + r2) × g) = 3,14 × (82 + 12 + (8 + 1) × 12,21) ≈ 549,15 см2

Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.

Источник