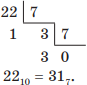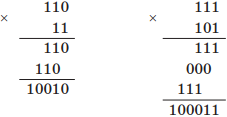за единицу измерения информации в теории кодирования принимается
Информатика. 7 класс
Конспект урока
Единицы измерения информации
Перечень вопросов, рассматриваемых в теме:
Каждый символ информационного сообщения несёт фиксированное количество информации.
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный объём сообщения определяется по формуле:
I – объём информации в сообщении;
К – количество символов в сообщении;
i – информационный вес одного символа.
Теоретический материал для самостоятельного изучения.
Любое сообщение несёт некоторое количество информации. Как же его измерить?
Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.
Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
Информационный вес одного символа этого алфавита составляет 4 бита.
Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.
Математически это произведение записывается так: I = К · i.
Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?
I = 180 · 5 = 900 бит.
Итак, информационный вес всего сообщения равен 900 бит.
В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.
I = 23 · 8 = 184 бита.
Значит, сообщение весит 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.
В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.
Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.
Разбор решения заданий тренировочного модуля
№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?
№2. Выразите в килобайтах 2 16 байтов.
2 6 = 64, а 2 10 байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.
№3. Тип задания: выделение цветом
8 х = 32 Кб, найдите х.
За единицу измерения информации в теории кодирования принимается
Электронные облака
Лекции
Рабочие материалы
Тесты по темам
Template tips
Задачи
Логика вычислительной техники и программирования
Лекция «Технология кодирования и измерения количества информации»
Качество и количество информации
Анализируя информацию, мы сталкиваемся с необходимостью определения качества и определения количества полученной информации. Определить качество информации чрезвычайно сложно, а часто и вообще невозможно. Какие-либо сведения, например исторические, могут десятилетиями считаться ненужными и вдруг их ценность может резко возрасти.
Вместе с тем определить количество информации не только можно, но и нужно. Это необходимо для того, чтобы сравнить друг с другом различные массивы информации, а также определить, какие размеры должны иметь материальные объекты (бумага, магнитные носители и т.д.), хранящие эту информацию.
Далее, говоря об измерении информации, мы будем иметь в виду определение ее количества.
Единая форма кодирования и измерения количества информации
Как измерять количество информации? Для этого нужно иметь универсальный способ, позволяющий представить любую ее форму (текстовую, графическую и др.) в едином стандартном виде.
За такой способ принята так называемая двоичная форма представления информации. Она заключается в записи любой информации в виде последовательности только двух символов: 0 и 1 (то есть в виде двоичных чисел) и с технической точки зрения наиболее проста и удобна (есть ток/нет тока, намагничено/размагничено, высокое напряжение/низкое напряжение).
Рассмотрим сначала одноразрядное двоичное число – бит. Оно может принимать два различных значения: 0 и 1
Если с помощью одноразрядного числа попробовать закодировать какую-либо информацию (например, ответ на вопрос «идет ли дождь?»), то мы успешно справимся с поставленной задачей, поскольку количество различных вариантов кодирования в данном случае равно двум (0-не идет, 1-идет).
К = 2 n °, где n – число разрядов двоичного числа.
В общем случае, верно, что чем больше различных видов однотипной информации требуется закодировать, тем больше разрядов двоичного числа (бит) требуется.
Единицы измерения информации
Таким образом, можно утверждать: информацию можно измерять в битах, то есть в количестве двоичных разрядов. Бит является наименьшей единицей измерения количества информации.
В 100 Мб можно уместить:
| Страниц текста | 50000 |
| Цветных слайдов высочайшего качества | 150 |
| Аудиозапись | 1,5 часа |
| Музыкальный фрагмент качества CD-стерео | 10 минут |
| Фильм высокого качества записи | 15 секунд |
| Протоколы операций по банковским счетам | За 1000 лет |
Представление текстовой информации в компьютере. Кодовые таблицы
Кодирование текстового сообщения
Каждому символу ставится в соответствие двоичное число, причем таким образом, что чем дальше символ расположен от начала алфавита, тем больше значение двоичного числа, которое является кодом данного символа. Сколько разрядов (бит) требуется, чтобы закодировать все буквы, знаки препинания, математические и специальные символы? Легко подсчитать:
Находим, что для кодирования всех символов необходимо 8-разрядное двоичное число. Каждому символу ставится в соответствие свое уникальное значение восьмиразрядного двоичного числа. Так, если 10000000 – код буквы А, а 10001100 – код буквы М, то слово «МАМА» кодируется последовательностью из 32-х двоичных цифр (бит):
10000000 10001100 10000000 10001100, именно в такой форме данное текстовое сообщение и будет закодировано компьютером с использованием ровно 32-х бит.
Таблица кодирования ASCII
Как мы уже выяснили, традиционно для кодирования одного символа используется 8 бит. И, когда люди определились с количеством бит, им осталось договориться о том, каким кодом кодировать тот или иной символ, чтобы не получилось путаницы, т.е. необходимо было выработать стандарт – все коды символов сохранить в специальной таблице кодов. В первые годы развития вычислительной техники таких стандартов не существовало, а сейчас наоборот, их стало очень много, но они противоречивы. Первыми решили эти проблемы в США, в Институте стандартизации. Этот институт ввел в действие таблицу кодов ASCII (American Standard Code for Information Interchange – стандартный код информационного обмена США).
Рассмотрим таблицу кодов ASCII:
Таблица ASCII разделена на две части. Первая – стандартная – содержит коды от 0 до 127. Вторая – расширенная – содержит символы с кодами от 128 до 255.
Первые 32 кода отданы производителям аппаратных средств и называются они управляющие, т.к. эти коды управляют выводом данных. Им не соответствуют никакие символы.
Коды с 32 по 127 соответствуют символам английского алфавита, знакам препинания, цифрам, арифметическим действиям и некоторым вспомогательным символам.
Коды расширенной части таблицы ASCII отданы под символы национальных алфавитов, символы псевдографики и научные символы.
Все буквы расположены в них по алфавиту, а цифры – по возрастанию. Этот принцип последовательного кодирования позволяет определить код символа, не заглядывая в таблицу.
Коды цифр берутся из этой таблицы только при вводе и выводе и если они используются в тексте. Если же они участвуют в вычислениях, то переводятся в двоичную систему счисления.
Альтернативные системы кодирования кириллицы
Таблица Unicode разделена на несколько областей. Область с кодами от 0000 до 007F содержит символы набора Latin 1 (младшие байты соответствуют кодировке ISO 8859-1). Далее идут области, в которых расположены знаки различных письменностей, а также знаки пунктуации и технические символы. Часть кодов зарезервирована для использования в будущем (29000). 6000 кодовых комбинаций оставлено программистам.
Символам кириллицы выделены коды в диапазоне от 0400 до 0451.
Использование Unicode значительно упрощает создание многоязычных документов, публикаций и программных приложений.
Решение задач
1. Закодируйте с помощью ASCII слово: МИР
Решение: открываем таблицу ASCII,
по таблице ищем букву М, её код 204
по таблице ищем букву И, её код 200
по таблице ищем букву Р, её код 208
Ответ: код слова МИР – 204 200 208
2. Декодируйте тексты, заданные десятичным кодом: 192 203 195 206 208 200 210 204
Решение: открываем таблицу ASCII, в таблице ищем коды и соответствующую им букву:
192 – А; 203 – Л; 195 – Г; 206 – О; 208 – Р; 200 – И; 210 – Т; 204 – М, т. е. получили слово: АЛГОРИТМ
Ответ: 192 203 195 206 208 200 210 204 – АЛГОРТИМ
3. Десятичный код буквы «I» в таблице ASCII равен 73. Не пользуясь таблицей, составьте последовательность кодов, соответствующих слову MIR
Решение: Зная, что все буквы расположены по алфавиту, а цифры по возрастанию делаем следующие выводы: I – 73, J – 74, K – 75, L – 76, M – 77, N – 78, O – 79, P – 80, Q – 81, R – 82
Ответ: MIR – 77 73 82
4. Каков информационный объём текста, содержащего слово МИР:
а) в 16-битовой кодировке; б) в 8-битовой кодировке
Решение:
Зная, что в 8-битовой кодировке 1 символ – 8 бит делаем следующие выводы:
МИР – 3 символа = 24 бит (3*8)
Зная, что в 16-битовой кодировке 1 символ – 16 бит делаем следующие выводы:
МИР – 3 символа = 48 бит (3*16)
Ответ: а) 48 бит; б) 24 бит.
5. Текст занимает полных 2 страницы. На каждой странице размещается 45 строк по 45 символов. Определить объём оперативной памяти, который займёт этот текст.
Кодирование графической информации
Общие понятия о графической информации
Графическая информация представляет собой изображение, сформированное из определенного числа точек – пикселей. Добавим к этой информации новые сведения. Процесс разбиения изображения на отдельные маленькие фрагменты (точки) называется пространственной дискретизацией. Ее можно сравнить с построением рисунка из мозаики. При этом каждой мозаике (точке) присваивается код цвета.
От количества точек зависит качество изображения. Оно тем выше, чем меньше размер точки и соответственно большее их количество составляет изображение. Такое количество точек называется разрешающей способностью и обычно существуют четыре основных значений этого параметра: 640×480, 800×600, 1024×768, 1280×1024.
Качество изображения зависит также от количества цветов, т.е. от количества возможных состояний точек изображения, т.к. при этом каждая точка несет большее количество информации. Используемый набор цветов образует палитру цветов.
Кодирование цвета
Рассмотрим, каким образом происходит кодирование цвета точек. Для кодирования цвета применяется принцип разложения цвета на составляющие. Их три: красный цвет (Red, R), синий (Blue, В) и зелёный (Green, G). Смешивая эти составляющие, можно получать различные оттенки и цвета – от белого до черного.
Сколько бит необходимо выделить для каждой составляющей, чтобы при кодировании изображения его качество было наилучшим?
Если рисунок черно-белый, то общепринятым на сегодняшний день считается представление его в виде комбинации точек с 256 градациями серого, т.е. для кодирования точки достаточно 1 байта.
Если же изображение цветное, то с помощью 1 байта можно также закодировать 256 разных оттенков цветов. Этого достаточно для рисования изображений типа тех, что мы видим в мультфильмах. Для изображений же живой природы этого недостаточно. Если увеличить количество байт до двух (16 бит), то цветов станет в два раза больше, т.е. 65536. Это уже похоже на то, что мы видим на фотографиях и на картинках в журналах, но все равно хуже, чем в живой природе. Увеличим еще количество байтов до трех (24 бита). В этом случае можно закодировать 16,5 миллионов различных цветов. Именно такой режим позволяет работать с изображениями наилучшего качества.
Количество бит, необходимое для кодирования цвета точки называется глубиной цвета. Наиболее распространенными значениями глубины цвета являются 4, 8, 16 и 24 бита на точку.
Решение задач
1. Какой объём видеопамяти необходим для хранения четырёх страниц изображения при условии, что разрешающая способность дисплея равна 640Х480 точек, а используемых цветов – 32?
Теперь все параметры нам известны, находим объём:
V = 640*480*5*4 =6144000 бит = 750 Кбайт (т.к. в 1 байте – 8 бит и в 1 Кбайте – 1024 байт)
Ответ: 750 Кбайт
2. 256-цветный рисунок содержит 1 Кбайт информации. Из скольки точек он состоит?
Переведём известный объём в биты: 1Кбайт = 1024 байт*8бит = 8192 бит
Зная глубину и объём находим количество точек на изображении: 8192:8 = 1024 точек
Кодирование звуковой информации
Оцифровка звука
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Для человека звук тем громче, чем больше амплитуда сигнала, и тем выше тон, чем больше частота сигнала. Непрерывный сигнал не несет в себе информации, поэтому он должен быть превращен в последовательность двоичных нулей и единиц – двоичный (цифровой) код.
Оцифровку звука выполняет специальное устройство на звуковой плате. Называется оно аналого-цифровой преобразователь (АЦП). Обратный процесс – воспроизведение закодированного звука производится с помощью цифро-аналогового преобразователя (ЦАП).
Весь процесс кодирования и декодирования представить в виде следующей схемы:
Схема кодирования звука:
В процессе кодирования непрерывного звукового сигнала производится дискретизация по времени, или, как говорят, «временная дискретизация». Звуковая волна разбивается на отдельные маленькие временные участки и для каждого участка устанавливается определенная величина амплитуд. Данный метод называется импульсно-амплитудной модуляцией РСМ Code Modulation).
Таким образом, гладкая кривая заменяется на последовательность «ступенек».. Каждой «ступеньке» присваивается значение громкости звука (1, 2, 3). Чем больше «ступенек», тем большее количество уровней громкости выделено в процессе кодирования, и тем большее количество информации будет нести значение каждого уровня и более качественным будет звучание.
Характеристики оцифрованного звука
Качество звука зависит от двух характеристик – глубины кодирования и частоты дискретизации. Рассмотрим эти характеристики.
Современные звуковые карты обеспечивают 16-битную глубину кодирования звука, и тогда общее количество различных уровней будет: N=2 16 = 65536.
Частота дискретизации (М) – это количество измерений уровня звукового сигнала в единицу времени. Эта характеристика показывает качество звучания и точность процедуры двоичного кодирования. Измеряется в герцах (Гц). Одно измерение за одну секунду соответствует частоте 1 Гц, 1000 измерений за одну секунду – 1 килогерц (кГц). Частота дискретизации звукового сигнала может принимать значения от 8 до 48 кГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD.
Высокое качество звучания достигается при частоте дискретизации 44,1 кГц и глубины кодирования звука, равной 16 бит. Для мрачного, приглушенного звука характерны следующие параметры: частота дискретизации – 11 кГц, глубина кодирования – 8 бит.
| Глубина кодирования | Частота дискретизации | |
| Радиотрансляция | 8 бит | До 8 кГц |
| Среднее качество | 8 бит или 16 бит | 8-48 кГц |
| Звучание CD-диска | 16 бит | До 48 кГц |
Для того, чтобы найти объем звуковой информации, необходимо воспользоваться следующей формулой:
V= M*I*t,
где М — частота дискретизации (в Гц),
I — глубина кодирования (в битах),
t — время звучания (в секундах).
Решение задач
1. Определить объём памяти для хранения моноаудиофайла, время звучания которого составляет пять минут при частоте дискретизации 44 кГц и глубине кодирования 16 бит.
Решение: Воспользуемся формулой: V = M*I*t
В нашем случае М = 44 кГц = 44000 Гц
I = 16 бит
t = 5 минут,
подставляем в формулу и получаем:
V = 44000*16*5 = 3520000 бит = 430 Кбайт (примерно)
Методы измерения количества информации
Теория к заданию 10 из ЕГЭ по информатике
Информация и ее кодирование
Различные подходы к определению понятия «информация». Виды информационных процессов. Информационный аспект в деятельности человека
Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:
Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.
Основными социально значимыми свойствами информации являются:
В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.
Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.
Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).
Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.
Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.
Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.
Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.
Язык как способ представления и передачи информации
Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.
В зависимости от способа восприятия знаки делятся на:
Для долговременного хранения знаки записывают на носители информации.
Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).
По способу связи между формой и значением знаки делятся на:
Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.
Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.
Методы измерения количества информации: вероятностный и алфавитный
Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:
Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:
I = log2 32 = 5 битов.
Если N не является целой степенью 2, то число log2N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log2N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.
Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:
N = 26; N’ = 32; I = log2N’ = log2(2 5 ) = 5 битов.
Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:
Примеры решения задач
Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log2101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log2128 = 7 битов. Для 80 измерений общий информационный объем равен:
80 · 7 = 560 битов = 70 байтов.
Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
$N$ — количество возможных событий;
Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Единицы измерения количества информации
Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).
Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.
В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.
Производные единицы измерения количества информации:
1 килобайт (Кб) = 1024 байта = 2 10 байтов
1 мегабайт (Мб) = 1024 килобайта = 2 20 байтов
1 гигабайт (Гб) = 1024 мегабайта = 2 30 байтов
1 терабайт (Тб) = 1024 гигабайта = 2 40 байтов
Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче
Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.
В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.
Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).
Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.
Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.
Примеры решения задач
Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.
Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 01002 = В416.
Скорость передачи информации и пропускная способность канала связи
Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.
Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.
Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.
Примеры решения задач
Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.
Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:
Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2 8 ⋅ 10 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = (2 8 ⋅ 125 ⋅ 2 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = 125 ⋅ 45 = 5625 Кбайт.
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$a$ — цифры численной записи, соответствующие разрядам;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 1310;
17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
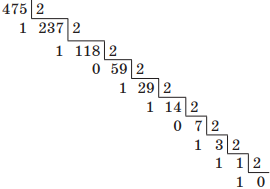
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –2 31 = –214748364810.
Максимальное положительное число равно
А = 2 31 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Формат с плавающей запятой
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
Число в экспоненциальном формате представляется в таком виде:
$q$ — основание системы счисления;
Например, десятичное число 2674,381 в экспоненциальной форме запишется так:
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.
Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.
Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 11111112 = 12710. Так как числа представляются в двоичной системе счисления, то
Аналогично, максимальное значение мантиссы равно
Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы
Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.
Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.
Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2 I = 2 8 = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:
Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.
В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2 16 = 65536 ). Коды символов могут принимать значение от 0 до 65535.
Примеры решения задач
Пример. С помощью кодировки Unicode закодирована следующая фраза:
Я хочу поступить в университет!
Оценить информационный объем этой фразы.
Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.