зачем нужно кодирование сообщений при передаче данных по сетевой среде

Сетевое кодирование

Сетевое кодирование — раздел теории информации изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах.

Содержание

Основы сетевого кодирования

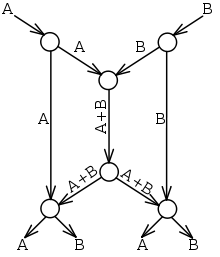
Узлы-получатели имеют возможность восстановить исходные пакеты из информации об одном полученном пакете и их комбинации. В результате увеличивается пропускная способность сети — по два пакета может быть передано двум получателям одновременно (за каждый такт), хотя минимальное сечение сети содержит всего три канала передачи данных.

Случайное сетевое кодирование

В качестве основного способа рассматривается включение в передаваемый пакет дополнительной информации, идентифицирующей пакет в рамках некоторой сессии (считается, что комбинироваться могут пакеты принадлежащие только одной сессии). Например, это может быть простое битовое поле. Для рассмотренной выше сети бабочка данное битовое поле может состоять из двух бит для каждого пакета:

Пакет	Битовое поле
	1 0
	0 1
	1 1

Первый получатель получит два пакета с битовыми полями «1 0» и «1 1», второй получатель — «0 1» и «1 1». Используя это поле как информацию о коэффициентах линейного уравнения для пакетов, получатель может восстановить исходные пакеты, если они были переданы без ошибок.

Защита информации от искажения

Рассматривая сеть «бабочка», можно показать, что для первого получателя вероятность принять пакет без ошибок больше, чем для пакета , даже если предположить одинаковые, но отличные от нуля вероятности ошибок в принятых получателем пакетах и .

Для того, чтобы уменьшить подобный эффект авторы предлагают модифицировать способ итеративного декодирования пакетов A и B (при, например, использовании LDPC-кодирования), когда итерации декодирования пакетов проводятся одновременно и декодеры обмениваются между собой об информации о вероятностях ошибок в конкретных битах пакетов. Для полного избавления от данного эффекта авторы предлагают также разбить исходные пакеты на несколько частей и передавать их различными путями. Как показал численный эксперимент, это действительно уравнивает вероятности декодирования пакетов.

Методы, используемые для декодирования в случайном сетевом кодировании, рассматривают все принятые пакеты как единый объект (часто — матрицу), построенной из принятых пакетов-строк. Если первая часть пакета представляет собой битовое поле, то операции с матрицей сводятся, во-первых, к приведению левой её части к диагональному виду (с помощью метода Гаусса), а затем к исправлению ошибок в правой части матрицы. Для исправления ошибок можно использовать ранговые коды, которые могут исправить не только ошибки в столбцах матрицы (из-за неправильно принятых битов данных), но и ошибки в строках матрицы (из-за ошибок передачи в битовом поле).

Источник

Инфокоммуникационные системы и сети (ИКСС)

Конспект лекций по теме 1.2

Структура локальных сетей

Отличительные признаки локальной вычислительной сети [1] :

-высокая скорость передачи информации (не менее 10 Мбит/с);

высокоэффективный, быстродействующий механизм управления обменом;

-регламентированное количество компьютеров, подключаемых к сети.

При таких свойствах понятно, что глобальные сети отличаются от локальных тем, что они рассчитаны на неограниченное число абонентов. Кроме того, они чаще всего используют не слишком качественные каналы связи и относительно низкую скорость передачи данных, а механизм управления обменом в этих сетях не может быть гарантированно быстрым.

Вместе с тем компьютерные сети имеют и существенные недостатки:

-сеть требует дополнительных, иногда значительных материальных затрат на покупку оборудования, сетевого программного обеспечения, на создание сетевой инфраструктуры и обучение персонала;

-сеть требует приема на работу специалиста (администратора сети), который будет заниматься обеспечением работоспособности сети, ее модернизацией, управлением доступом к сетевым ресурсам, устранением неисправностей, защитой информации, резервным копированием и архивированием данных;

-проводная сеть ограничивает возможности перемещения компьютеров, подключенных к ней, так как в этом случае может понадобиться перекладка соединительных кабелей;

-сеть является средой для распространения компьютерных вирусов, поэтому вопросам защиты от них придется уделять больше внимания, чем в случае автономного использования компьютеров;

-сеть значительно повышает риск несанкционированного доступа к информации (информационная защита требует проведения комплекса, соответствующих организационных и технических мероприятий).

Основные определения и термины

Клиентом называется абонент сети, который только использует сетевые ресурсы, но сам свои ресурсы в сеть не отдает. Компьютер-клиент также называют рабочей станцией.

[1] Кондратенко С., Новиков Ю. Основы локальных сетей [Электронный ресурс]

[2] Бабешко, В.Н. Распределенные информационно-вычислительные системы в туманных вычислительных сетях.

Источник

Кодирование и Шифрование

В наш век интернет-технологий, когда мы доверяем все свои данные интернет-сервисам, нужно знать и понимать, как они их хранят и обрабатывают.

Но зачем это вообще нужно знать? Чтобы попросту не попасть в ситуацию, когда ваши личные данные, пароли от аккаунтов или банковских карт окажутся в руках мошенников. Как говорится: «Доверяй, но проверяй»

Важные аспекты в хранении данных, будь то на внешних серверах или домашнем компьютере, – это прежде всего кодирования и шифрование. Но чем они отличаются друг от друга? Давайте разбираться!

Ни для кого не секрет, что компьютер может хранить информацию, но он не может хранить её в привычной для нас форме: мы не сможем просто так написать на флешки реферат, не можем нарисовать на жестком диске картинку так, чтобы её мог распознать компьютер. Для этого информацию нужно преобразовать в язык понятный компьютеру, и именно этот процесс называется кодированием. Когда мы нажимаем на кнопку на клавиатуре мы передаем код символа, который может распознать компьютер, а не сам символ.

Определения и различия

Кодирование – процесс преобразования доступной нам информации в информацию понятную компьютерную.

Шифрование – процесс изменения информации таким образом, чтобы её смогли получить только нужные пользователи.

Шифрование применялось и задолго до создания компьютеров и информатики как таковой. Но зачем? Цели её применения можно было понять из определения, но я опишу их ещё раз более подробно. Главные цели шифрования это:

конфиденциальность – данные скрыты от посторонних

целостность – предотвращение изменения информации

идентифицируемость – возможность определить отправителя данных и невозможность их отправки без отправителя

Оценить стойкость шифра можно с помощью криптографической стойкости.

Криптографическая стойкость – это свойство шифра противостоять криптоанализу, изучению и дешифровки шифра.

Криптостойкость шифра делится на две основные системы: абсолютно стойкие системы и достаточно стойкие системы.

Абсолютно стойкие системы – системы не подверженные криптоанализу. Основные критерии абсолютно стойких систем:

Ключи должны генерироваться для каждого сообщения отдельно

Генерация ключей независима

Длина ключа должна быть не меньше длины сообщения

К сожалению, такие системы не удобны в своём использовании: появляется передача излишней информации, которая требует мощных и сложных устройств. Поэтому на деле применяются достаточно стойкие системы.

Достаточно стойкие системы – системы не могут обеспечить полную защиту данных, но гораздо удобнее абсолютно стойких. Надежность таких систем зависит от возможностей крипто аналитика:

Количества перехваченных сообщений

Времени и вычислительных способностей

А также от вычислительной сложности шифра.

Вычислительная сложность – совокупность времени работы шифрующей функции, объема входных данных и количества используемой памяти. Чем она больше, тем сложнее дешифровать шифр.

История шифрования

Шифрование берет своё начало ещё из древних времен. Примерно 1300 лет до нашей эры был создан один из первых методов шифрования – Атбаш. Принцип шифрования заключается в простой подставке символов по формуле:, где:

n – количество символов в алфавите

i – порядковый номер символа.

С тех самых пор шифрование активно развивалось вместе с развитием нашей цивилизации

Хоть шифры и менялись, но их принцип нет – для расшифровки сообщения требуется ключ. В случае с Абашем ключом может считать последовательность порядковых номеров исходных символов, но этот ключ ещё надо как-то передать. Методы шифрования, которые используются сейчас, научились-таки передавать ключи по открытым и незащищённым каналам связи. Казалось бы, передача ключей шифрования по обычным каналам — это добровольное жертвование своими данными, но не всё так просто. Разберём это на примере популярного алгоритма шифрования «RSA», разработанного в 1977 году.

Первым делом выбирается два случайный простых числа, которые перемножаются друг на друга – именно это и есть открытый ключ.

К слову: Простые числа — это те числа, которые могут делиться без остатка либо на 1, либо на себя.

Длина таких чисел может быть абсолютно любая. К примеру, возьмем два простых числа 223 и 13. Их произведение 2899 – будет являться открытым ключом, который мы и будем передавать по открытому каналу связи. Далее нам необходимо вычислить функцию «Эйлера» для произведения этих чисел.

Функция Эйлера – количество натуральных чисел, меньших чем само число и, которые будут являть взаимно простыми числами с самим числом.

Возможно, звучит непонятно, но давайте это разберем на небольшом примере:

φ (26) [фи от двадцати шести] = какому-то числу чисел, которое всегда будет меньше 26, а сами числа должны иметь только один общий делитель единицу с 26.

1 – подходит всегда, идем дальше;

7 – только на 1 – подходит;

Общее количество таких чисел будет равно 12. А найти это число можно по формуле: φ(n*k) = (n-1)(k-1) в нашем случае 26 можно представить как 2 * 13, тогда получим φ(26) = φ(2 * 13) = (2-1)*(13-1) = 1 * 12 = 12

Теперь, когда мы знаем, что такое функция Эйлера и умеем её вычислять найдем её для нашего открытого ключа – φ(2899) = φ(223 * 13) =(223 – 1)*(13-1) = 222 * 12 = 2664

После чего нам нужно найти открытую экспоненту. Не пугайтесь, тут будет гораздо проще чем с функцией «Эйлера».

Открытая экспонента – это любое простое число, которое не делится на функцию Эйлера. Для примера возьмем 13. 13 не делится нацело на число 2664. Вообще открытую экспоненту лучше выбирать по возрастанию простым перебором, а не просто брать случайную. Так для нашего примера разумнее было бы взять число 5, но давайте рассмотрим на примере 13

e – открытая экспонента

mod – остаток отделения

В обоих случаях у нас получится число 205

На этом подготовка отправки сообщения успешно завершается и начинается самое веселое – отправка данных для дешифрования сообщения. На этом шаге мы отправляем открытый ключ и открытую экспоненту человеку, сообщение которого хотим получить. Предположим, что в этот момент наш ключ и экспоненту перехватили 3-е лица, но до нужного нам человека они всё так же дошли

Теперь этому человеку нужно отправить нам сообщение, для простоты предположим, что это какое-то число, например: 92. Для этого ему нужно отправить нам остаток от деления 92 в степени открытой экспоненты на открытый ключ – T ^ e mod n , где

T – шифруемый текст

e – открытая экспонента

mod – остаток от деления

Предположим, что и в этот раз сообщение перехватили, но нам оно всё так же дошло

С – зашифрованный текст

d – закрытая экспонента

mod – остаток от деления

235 ^ 205 mod 2899 = 92.

Вуаля, и мы имеет исходное число. Но, что насчет перехваченных сообщений? У злоумышленника есть сообщение, ключ и экспонента, но как мы помни для дешифровки ему ещё нужна секретная экспонента, она же секретный ключ, но для того, чтобы вычислить её, ему придется разложить исходный ключ 2899 на множители, а сделать это не так уж и просто, особенно когда вместо двух чисел 223 и 13, будут использовать числа длиной несколько десятков символов

Но ничто в мире не идеально, в том числе и этот метод.

Его первый недостаток – это подборка пары чисел для открытого ключа. Нам нужно не просто сгенерировать случайно число, но ещё и проверить на то простое ли оно. На сегодняшний нет методов, которые позволяют делать это сверх быстро.

Второй недостаток – так же связан с генерацией ключа. Как мы с вами помним: «ключи должны генерировать независимо от каких-либо факторов», но именно это правило нарушается, когда мы пытается сгенерировать строго простые числа.

Третий недостаток – подбор и перебор чисел для экспонент.

Четвертый – длина ключей. Чем больше длина, тем медленнее идет процесс декодирования, поэтому разработчики пытаются использовать наименьшие по длиннее ключи и экспоненты. Даже я акцентировал на это внимание, когда говорил, что лучше взять число 5, вместо 13 для открытой экспоненты. Именно из-за этого и происходит большая часть взломов и утечек данных

Но не стоит печалиться, ведь как я и говорил: криптография и шифрование развивается вместе с развитием цивилизации. Поэтому довольно скоро все мы будем шифровать свои данные с помощью Квантового шифрование.

Этот метод основывается на принципе квантовой суперпозиции – элементарная частица может сразу находится в нескольких положениях, иметь разную энергию или разное направление вращения одновременно. По такому принципу и работает передача ключей шифрования по протоколу BB-84.

Есть оптоволокно, по которому передаются единичные фотоны света. Мы, как отправитель может сгенерировать абсолютно любой двоичный ключ, по тому же принципу квантовой супер позиции, ну или использовать обычные генераторы псевдослучайных чисел. Допустим мы хотим передать ключ 101001011. Для этого нам нужно принять за обозначение какое положение фотона соответствует единице, а какое нулю. Представим, что вертикальное положение – это 1, а горизонтальное – 0. Если оставить все так, то от передачи ключей таким образом не будет никакого смысла, ведь тогда злоумышленник всегда сможет измерить фотон, получить его значение, создать и отправить точно такой же обратно человеку, которому мы хоти передать ключ. Поэтому были введены ещё два положение – диагональные. Предоставим вертикальную волну, или же значение 1 и отклоним её на 45 градусов влево. Это будет вторая единица. Вернемся обратно и отклоним на 45 градусов вправо – это будет второй 0.

Вернемся к нашему ключу 101001011. Мы случайным образом выбираем направление – обычное или диагональное. Для удобства присвоим обычному номер 1, а диагональному 2.

Давайте отправим ключ – 1(1), 0(2), 1(1), 0(1), 0(1), 1(2), 0(2), 1(1), 1(2). Теперь человеку, которому мы отправляем ключ, нужно точно так же, совершенно случайно, выбрать случайное направление.

Допустим он выбрал направления: 221111212. Поскольку есть всего 2 плоскости отправки: 1 и 2, они же называются: канонический и диагональный базис, то шанс того, что он выбрал правильные направления 50%.

Если он угадал базис – он получил верное значение, если нет – неверное. Учитывая его направления, он получил: 001000011. Теперь нужно отсеять неправильные значения: можно сделать это обменом базисов по любому, даже не защищенному, каналу связи. После этого у нас обоих останется ключ: 0100011. Теперь с помощью его мы можем передавать и кодировать сообщения по обычному методу шифрования.

Заключение

Причитав и разобрав эту статью, мы с вами узнали, чем отличается кодирование от шифрования, их историю с будущим, узнали каким должен быть идеальный шифр и немного поговорили про крипто анализ. Уже с этими знаниями, которые были предоставлены в этой статье, можно спокойно идти и делать какую-нибудь систему авторизации или пытаться взломать какой-то сайт, главное не перебарщивать.

Источник

Сетевое кодирование

Статья опубликована в №5 (671) от 17 февраля

Когда речь идет о повышении пропускной способности сети, то обычно говорят о более быстрых интерфейсах, агрегировании трафика, плотном мультиплексировании и других аппаратных решениях. Однако поднять производительность сети (речь идет не о повышении скорости работы сетевых приложений) можно и без радикальных изменений в инфраструктуре. Одним из способов достичь этого является сетевое кодирование, которое особенно эффективно при многоадресных передачах.

Рис. 1. Простой пример сетевого кодирования

Сегодня сетевые коммуникации базируются на одном и том же фундаментальном принципе работы. Во всех случаях, будь-то передача пакетов через Интернет или сигналов по телефонной сети, информация транспортируется подобно тому, как автомобили разделяют автомагистраль или потоки – трубопровод. Другими словами, потоки данных могут использовать общие сетевые ресурсы, однако информация в них не смешивается. Маршрутизация, хранение данных, контроль ошибок и в конечном итоге все сетевые функции основываются на этом предположении.

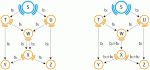Рис. 2. Многоадресная передача в коммуникационной сети.

Данную концепцию нарушает сетевое кодирование (network coding) – новое направление в теории информации, позволяющее достичь максимального потока информации в сети. Оно предполагает, что узлы вместо обычной передачи пакетов могут комбинировать несколько входных пакетов в один или в несколько выходных. Эту идею можно проиллюстрировать простым примером из беспроводных коммуникаций. На рис. 1 узлы А и В хотят обменяться пакетами через базовую станцию S. При традиционном методе А и В посылают S соответственно пакеты а и b, а затем S выполняет их широковещательную рассылку. Таким образом, узел А (соответственно узел В) получает ненужный ему собственный пакет, а обмен пакетами занимает четыре цикла передачи. При использовании сетевого кодирования станция S, получив пакеты a и b, посылает результат выполнения над ними операции XOR (исключительное ИЛИ). Узлы затем могут извлечь интересующие их пакеты из результирующего, а обмен данными выполняется только за три цикла.

Линейное сетевое кодирование в общем похоже на этот пример, с той лишь разницей, что операция XOR заменяется линейной комбинацией данных, интерпретируемых как числа из конечного поля (необходимые сведения из алгебры будут приведены ниже). Сетевое кодирование повышает эффективную пропускную способность сети, оно также подходит для тех случаев, когда решение принимается на основе неполной или неопределенной информации. Подобно кодированию в каналах со стиранием успешный прием информации здесь не зависит от получения специфического содержания пакета, а скорее от получения достаточного количества независимых пакетов.

Следует, конечно, отметить, что сетевое кодирование требует повышенных вычислительных возможностей узлов. Однако закон Мура приводит к понижению стоимости вычислений, а проблемы современных сетей вызываются в основном недостаточной пропускной способностью. Таким образом, линейное кодирование использует дешевые вычислительные мощности для увеличения эффективности сетей.

Для понимания дальнейшего нам необходимы некоторые сведения из абстрактной алгебры, приведенные здесь в минимальном объеме и без излишней строгости.

Конечные поля

Можно было бы сразу дать определение конечного поля, однако для удобства дальнейшего изложения введем сначала понятие группы.

Прежде всего приведем следующее:

Определение 1. Соответствие, в силу которого каждой паре а и b элементов множества М, взятых в данном порядке, соответствует третий элемент с того же множества М, называется алгебраической операцией, определенной в М.

Обычно это записывается в виде ab = c. Примерами алгебраических операций могут служить четыре известных арифметических действия на множестве всех действительных чисел, причем в случае деления нужно исключить число 0.

В одном и том же множестве может быть задано несколько алгебраических операций. Рассматривая множества с одной алгебраической операцией, мы приходим к первому из основных понятий современной алгебры – к понятию группы.

Определение 2. Непустое множество G называется группой, если в нем определена алгебраическая операция, называемая умножением, которая каждым двум элементам a и b из G ставит в соответствие элемент ab = с также из G, называемый их произведением. Выполняются также следующие аксиомы:

Если для любых двух элементов группы a и b выполняется равенство ab = ba, то такая группа называется коммутативной, или абелевой. Часто групповая операция в коммутативных группах обозначается знаком «+», и группу называют аддитивной. Примерами могут служить все целые, все рациональные и все действительные числа с операцией арифметического сложения, играющего роль групповой операции умножения. Другой простой пример группы – множество всех рациональных (и действительных) чисел (исключая число 0) с операцией арифметического умножения.

Опираясь на понятие группы, приведем теперь упрощенное определение поля.

Определение 3. Непустое множество F называется полем, если в нем определены две алгебраические операции: сложение и умножение, такие, что для них выполняются все свойства соответствующих арифметических операций (коммутативность и ассоциативность относительно сложения, коммутативность и ассоциативность относительно умножения, дистрибутивность умножения относительно сложения), и все элементы F являются группой относительно сложения, а все ненулевые элементы F – группой относительно умножения. Называются они соответственно аддитивной и мультипликативной группами поля F.

Полями, как нетрудно видеть, являются множества всех рациональных и действительных чисел со сложением и умножением в качестве алгебраических операций.

Нам понадобится еще определить отношение эквивалентности на множестве целых чисел, которое называется сравнением по модулю натурального числа.

Определение 4. Говорят, что два целых числа a и b сравнимы по модулю натурального числа n и записывают a = b (mod n), если при делении на n они дают одинаковые остатки. К примеру, 7 = 2 (mod 5).

Поле GF(2) содержит два элемента: 0 и 1. Операции в этом поле определяются следующим образом:

Как видно, алгебраическая операция сложение и обратная ей вычитание идентичны и выполняются посредством оператора XOR, а умножения – AND. Поскольку 1 является единственным обратным элементом в мультипликативной группе, то операция деления совпадает с умножением.

Для дальнейшего особо интересны поля типа GF(2 n ). Их элементы могут быть представлены в виде двоичных чисел. Для поля GF(2 8 ) это будут октеты, или байты, к примеру <01010011>, <11001010>и т. п. Операция сложения выполняется посредством применения оператора XOR к битам, находящимся на одинаковых позициях: <01010011>+ + <11001010>= <10011001>.

Сложение выполняется обычным методом с приведением коэффициентов по модулю 2. Умножение двух полиномов P и Q может быть выполнено следующим образом. Сначала находится их произведение W = P • Q, а затем вычисляется остаток по модулю R.

Для поля GF(2 8 ) первому двоичному символу из вышеприведенного примера соответствует полином x 6 + x 4 + x + 1, а второму – полином x 7 + x 6 + x 3 + x. Примером неприводимого полинома для этого поля может служить x 8 + x 4 + x 3 + x + 1.

На этом мы окончим необходимое математическое вступление и перейдем непосредственно к вопросу.

. Что такое сетевое кодирование?

Для наших целей достаточно ограничиться линейным сетевым кодированием.

Рассмотрим систему, действующую как ретранслятор информации, такой как маршрутизатор, узел в произвольной сети или узел в одноранговой распределенной сети. Обычно, когда пакет с данными достигает некоторого другого узла, тот просто повторяет его. Как уже упоминалось выше, при сетевом кодировании предполагается, что узел образует некую комбинацию из полученных пакетов и создает один или несколько выходных пакетов.

Предположим, что каждый пакет содержит L бит. Если комбинируемые пакеты имеют не одинаковые размеры, то меньшие дополним хвостовыми нулями. Мы будем интерпретировать s последовательных битов пакета как символ над полем GF(2 s ), а каждый пакет – как вектор, содержащий L/s символов. При линейном кодировании выходной пакет является линейной комбинацией полученных пакетов, где операция сложения выполняется над полем GF(2 s ). Смысл выбора линейной комбинации заключается в том, что при этом алгоритмы кодирования и декодирования весьма прозрачны.

Следует заметить, что линейная комбинация пакетов не является их конкатенацией: если мы образуем линейную комбинацию пакетов длины L, то результирующий пакет также имеет длину L. Рассмотрим теперь непосредственно процедуру линейного кодирования.

,

где суммирование выполняется по каждой позиции символа. Другими словами,

,

,

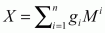
Кодирование может выполняться рекурсивно, а именно, применяться к уже закодированным пакетам. Рассмотрим теперь вкратце принципы декодирования.

,

Альтернативный подход заключается в детерминистических алгоритмах выбора комбинаций. Так, разработаны алгоритмы для многоадресных рассылок с полиномиальным временем работы, которые последовательно рассматривают узлы сети и решают, какую линейную комбинацию должен выбрать каждый из них. Так как любой из узлов использует фиксированный набор коэффициентов, то передавать необходимо только информационный вектор.

Как уже упоминалось выше, декодирование требует решения системы линейных уравнений. На практике это может быть выполнено следующим образом. Узел хранит закодированные векторы, которые он получает, а также собственные оригинальные пакеты строка за строкой в так называемой декодирующей матрице. Первоначально в ней содержатся только незакодированные (оригинальные) пакеты, которые этот узел должен отослать, и соответствующий кодирующий вектор. Когда поступает закодированный пакет, он вставляется в качестве последней строки в декодирующую матрицу. Затем матрица преобразуется к треугольному виду с помощью метода исключения Гаусса. Как только в матрице получится строка в форме e_i, то этот узел знает, что x равен оригинальному пакету M_i. Это происходит в самом конце, когда получено n линейно независимых закодированных векторов. Заметим, что декодирование выполняется не всеми узлами сети, а только получателями.

Какова польза от сетевого кодирования?

Основная причина, по которой вспыхнул интерес к сетевому кодированию, заключалась в том, что оно может увеличить емкость сети при многоадресной рассылке.

Эварист Галуа (1811—1832)

Представим сеть как ориентированный граф (в типичном случае это проводная сеть). Пусть вершины графа соответствуют терминалам, а ребра – каналам. Предположим, что у нас имеется М источников, каждый из которых посылает данные при некоторой заданной скорости, и N приемников. Все приемники хотят принимать пакеты от всех источников. Приведем весьма интересную теорему и примем ее без доказательства.

Теорема. Предположим, что скорости передачи пакетов источниками таковы, что без сетевого кодирования сеть может изолированно поддерживать любой из приемников (т. е. этот приемник может получать пакеты всех источников, как если бы он был единственным в сети). Тогда при подходящем выборе коэффициентов линейного кодирования сеть может поддерживать все приемники одновременно.

Сетевое кодирование может обеспечивать повышение пропускной способности сети не только в случае многоадресных потоков, но также и для одноадресных.

Особенно эффективно сетевое кодирование для обеспечения надежности и адаптивности сети. Обратимся снова к рис. 1 и предположим, что узлы A и B могут переходить в спящий режим или выйти за зону досягаемости без оповещения станции S. Если базовая станция S широковещательно передает пакет a (или b), он может быть полностью потерян, так как адресат может его не получить. Однако если базовая станция широковещательно отправит пакет a XOR b или, более общо, случайную линейную комбинацию информационных пакетов, передача доставит новую информацию всем активным узлам.

Вероятно, одним из наиболее известных приложений, использующих сетевое кодирование, является одноранговая (peer-to-peer) сеть Avalanche. В ней файл, который должен распределяться, расщепляется на небольшие блоки. Однако узлы вместо простой передачи блоков передают их случайную линейную комбинацию вместе со случайными коэффициентами данной линейной комбинации. Этим устраняется необходимость для каждого узла иметь полную информацию о распределении блоков в сети.

Небольшое заключение

Конечно, читатель вправе высказать некоторое недоумение по поводу того, что статья несколько перегружена математикой. С другой стороны, для понимания, что представляют собой современные сети, полезно знать, как уже упоминалось выше, что это не только оптоволоконные и медные кабели, радиопередатчики, коммутационные фабрики, порты и интерфейсы, но и весьма изысканная математика. Представьте себе, аппарат, созданный для исследования проблемы решения алгебраических уравнений в радикалах в 1831 г., более чем через 170 лет находит применение в информационных технологиях.

В связи с этим необходимо сказать несколько слов о его создателе, безусловно гениальном французском математике Эваристе Галуа (род. в 1811 г.), жизнь которого можно сравнить с падающей звездой. В возрасте 20 лет он дал исчерпывающий ответ на вопрос, три века бывший вызовом для математиков всего мира. Хотя понятие группы впервые появилось в работах Лагранжа и Руфини, сам термин «группа» был введен Галуа. Его идеи оказались плодотворными во всех областях математики и теоретической физики. Он погиб на дуэли в 1832 г., причем ни причина дуэли, ни его противник достоверно неизвестны.

Вы можете подписаться на нашу страницу в LinkedIn!

Напечатать Отправить другу

Источник