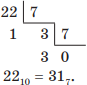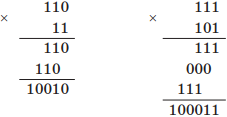задача кодирования источников информации
Практическая работа «Кодирование и декодирование информации. Решение задач»
Новые аудиокурсы повышения квалификации для педагогов
Слушайте учебный материал в удобное для Вас время в любом месте
откроется в новом окне
Выдаем Удостоверение установленного образца:
Тема: «Кодирование и декодирование информации. Решение задач»
Цель работы: Получить навыки кодирования и декодирования информации
Требования к оформлению работы:
Название практического занятия;
Ответы на контрольные вопросы;
Вывод о проделанной работе.
1. Изучить теорию по теме «Теория кодирования»
4. Ответить на контрольные вопросы:
5. Что изучает теория кодирования?
6. Объясните термины: кодирование и декодирование.
8. В чем заключается алфавитное кодирование?
9. Как кодируются тексты?
10. Как кодируются изображения?
11. Как кодируются звук и видео?
Теория кодирования – это раздел теории информации, изучающий способы отождествления сообщений с отражающими их сигналами. Задачей теории кодирования является согласование источника информации с каналом связи.
Объектом кодирования служит как дискретная, так и непрерывная информация, которая поступает к потребителю через источник информации. Понятие кодирование означает преобразование информации в форму, удобную для передачи по определенному каналу связи.
Обратная операция – декодирование – заключается в восстановлении принятого сообщения из закодированного вида в общепринятый, доступный для потребителя.
В теории кодирования существует ряд направлений:
— статическое или эффективное кодирование;
С появлением управляющих систем, в частности ЭВМ, роль кодирования существенно возросла и изменилась, так как без кодирования невозможна передача информации. В последнее время в связи с развитием телекоммуникационных систем и широким использованием вычислительной техники для обработки и хранения информации возникла новая область знаний – информационная безопасность.
Кодированием называют универсальный способ отображения информации при ее хранении, обработке и передаче в виде системы соответствий между сигналами и элементами сообщений, при помощи которых эти элементы можно зафиксировать.
Код – это правило однозначного преобразования сообщения из одной символической формы представления сообщения в другую, обычно без каких-либо потерь информации.
Если все кодовые слова имеют одинаковую длину, то код называется равномерным, или блочным.
Под абстрактным алфавитом будем понимать упорядоченное дискретное множество символов.
Алфавитное кодирование. Алфавитное, т.е. побуквенное, кодирование можно задать таблицей кодов. Фактически кодом преобразования является некоторая подстановка.
Тогда 


Компьютерная обработка данных основана на применении двоичного кода. Этот универсальный способ кодирования годится для любых данных, независимо от их происхождения и содержания.
Мощность алфавита в системе кодирования UNICODE составляет 216=65 536 разных кодов, из которых 63 484 кода соответствуют символам большинства алфавитов, а оставшиеся 2048 кодов разделены пополам и образуют таблицу размером 1024 столбцов х 1024 строк. В этой таблице более миллиона ячеек, в которых можно разместить еще более миллиона различных символов. Это символы «мертвых» языков, а также символы, не имеющие лексического содержания, указатели, знаки и т.п. Для записи этих дополнительных символов необходима пара 16-разрядных слов (16 разрядов для номера строки и 16 разрядов для номера столбца).
Таким образом, система UNICODE является универсальной системой кодирования всех символов национальных письменных систем и обладает возможностью существенного расширения.
Каждый пиксель на экране состоит из трех близко расположенных элементов, светящихся этими цветами.
Код цвета пикселя содержит информацию о доле каждого базового цвета.
Если все три составляющих имеют одинаковую интенсивность (яркость), то из их сочетаний можно получить 8 различных цветов:
Кодирование информации
Код — система условных знаков (символов) для передачи, обработки и хранения информации (сообщения).
Кодирование — процесс представления информации (сообщения) в виде кода.
Все множество символов, используемых для кодирования, называется алфавитом кодирования. Например, в памяти компьютера любая информация кодируется с помощью двоичного алфавита, содержащего всего два символа: 0 и 1.
Научные основы кодирования были описаны К.Шенноном, который исследовал процессы передачи информации по техническим каналам связи (теория связи, теория кодирования). При таком подходе кодирование понимается в более узком смысле: как переход от представления информации в одной символьной системе к представлению в другой символьной системе. Например, преобразование письменного русского текста в код азбуки Морзе для передачи его по телеграфной связи или радиосвязи. Такое кодирование связано с потребностью приспособить код к используемым техническим средствам работы с информацией (см. “Передача информации”).
Декодирование — процесс обратного преобразования кода к форме исходной символьной системы, т.е. получение исходного сообщения. Например: перевод с азбуки Морзе в письменный текст на русском языке.
В более широком смысле декодирование — это процесс восстановления содержания закодированного сообщения. При таком подходе процесс записи текста с помощью русского алфавита можно рассматривать в качестве кодирования, а его чтение — это декодирование.
Цели кодирования и способы кодирования
Способ кодирования одного и того же сообщения может быть разным. Например, русский текст мы привыкли записывать с помощью русского алфавита. Но то же самое можно сделать, используя английский алфавит. Иногда так приходится поступать, посылая SMS по мобильному телефону, на котором нет русских букв, или отправляя электронное письмо на русском языке из-за границы, если на компьютере нет русифицированного программного обеспечения. Например, фразу: “Здравствуй, дорогой Саша!” приходится писать так: “Zdravstvui, dorogoi Sasha!”.
Существуют и другие способы кодирования речи. Например, стенография — быстрый способ записи устной речи. Ею владеют лишь немногие специально обученные люди — стенографисты. Стенографист успевает записывать текст синхронно с речью говорящего человека. В стенограмме один значок обозначал целое слово или словосочетание. Расшифровать (декодировать) стенограмму может только стенографист.
Приведенные примеры иллюстрируют следующее важное правило: для кодирования одной и той же информации могут быть использованы разные способы; их выбор зависит от ряда обстоятельств: цели кодирования, условий, имеющихся средств. Если надо записать текст в темпе речи — используем стенографию; если надо передать текст за границу — используем английский алфавит; если надо представить текст в виде, понятном для грамотного русского человека, — записываем его по правилам грамматики русского языка.
Еще одно важное обстоятельство: выбор способа кодирования информации может быть связан с предполагаемым способом ее обработки. Покажем это на примере представления чисел — количественной информации. Используя русский алфавит, можно записать число “тридцать пять”. Используя же алфавит арабской десятичной системы счисления, пишем: “35”. Второй способ не только короче первого, но и удобнее для выполнения вычислений. Какая запись удобнее для выполнения расчетов: “тридцать пять умножить на сто двадцать семь” или “35 х 127”? Очевидно — вторая.
Однако если важно сохранить число без искажения, то его лучше записать в текстовой форме. Например, в денежных документах часто сумму записывают в текстовой форме: “триста семьдесят пять руб.” вместо “375 руб.”. Во втором случае искажение одной цифры изменит все значение. При использовании текстовой формы даже грамматические ошибки могут не изменить смысла. Например, малограмотный человек написал: “Тристо семдесять пят руб.”. Однако смысл сохранился.
В некоторых случаях возникает потребность засекречивания текста сообщения или документа, для того чтобы его не смогли прочитать те, кому не положено. Это называется защитой от несанкционированного доступа. В таком случае секретный текст шифруется. В давние времена шифрование называлось тайнописью. Шифрование представляет собой процесс превращения открытого текста в зашифрованный, а дешифрование — процесс обратного преобразования, при котором восстанавливается исходный текст. Шифрование — это тоже кодирование, но с засекреченным методом, известным только источнику и адресату. Методами шифрования занимается наука под названием криптография (см. “Криптография”).
История технических способов кодирования информации
С появлением технических средств хранения и передачи информации возникли новые идеи и приемы кодирования. Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе. Телеграфное сообщение — это последовательность электрических сигналов, передаваемая от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Эти технические обстоятельства привели С.Морзе к идее использования всего двух видов сигналов — короткого и длинного — для кодирования сообщения, передаваемого по линиям телеграфной связи.
Сэмюэль Финли Бриз Морзе (1791–1872), США
Такой способ кодирования получил название азбуки Морзе. В ней каждая буква алфавита кодируется последовательностью коротких сигналов (точек) и длинных сигналов (тире). Буквы отделяются друг от друга паузами — отсутствием сигналов.
Самым знаменитым телеграфным сообщением является сигнал бедствия “SOS” (Save Our Souls — спасите наши души). Вот как он выглядит в коде азбуки Морзе, применяемом к английскому алфавиту:
Три точки (буква S), три тире (буква О), три точки (буква S). Две паузы отделяют буквы друг от друга.
На рисунке показана азбука Морзе применительно к русскому алфавиту. Специальных знаков препинания не было. Их записывали словами: “тчк” — точка, “зпт” — запятая и т.п.
Характерной особенностью азбуки Морзе является переменная длина кода разных букв, поэтому код Морзе называют неравномерным кодом. Буквы, которые встречаются в тексте чаще, имеют более короткий код, чем редкие буквы. Например, код буквы “Е” — одна точка, а код твердого знака состоит из шести знаков. Это сделано для того, чтобы сократить длину всего сообщения. Но из-за переменной длины кода букв возникает проблема отделения букв друг от друга в тексте. Поэтому приходится для разделения использовать паузу (пропуск). Следовательно, телеграфный алфавит Морзе является троичным, т.к. в нем используется три знака: точка, тире, пропуск.
Равномерный телеграфный код был изобретен французом Жаном Морисом Бодо в конце XIX века. В нем использовалось всего два разных вида сигналов. Не важно, как их назвать: точка и тире, плюс и минус, ноль и единица. Это два отличающихся друг от друга электрических сигнала. Длина кода всех символов одинаковая и равна пяти. В таком случае не возникает проблемы отделения букв друг от друга: каждая пятерка сигналов — это знак текста. Поэтому пропуск не нужен.
Жан Морис Эмиль Бодо (1845–1903), Франция
Код Бодо — это первый в истории техники способ двоичного кодирования информации. Благодаря этой идее удалось создать буквопечатающий телеграфный аппарат, имеющий вид пишущей машинки. Нажатие на клавишу с определенной буквой вырабатывает соответствующий пятиимпульсный сигнал, который передается по линии связи. Принимающий аппарат под воздействием этого сигнала печатает ту же букву на бумажной ленте.
В современных компьютерах для кодирования текстов также применяется равномерный двоичный код (см. “Системы кодирования текста”).
Методические рекомендации
Тема кодирования информации может быть представлена в учебной программе на всех этапах изучения информатики в школе.
В пропедевтическом курсе ученикам чаще предлагаются задачи, не связанные с компьютерным кодированием данных и носящие, в некотором смысле, игровую форму. Например, на основании кодовой таблицы азбуки Морзе можно предлагать как задачи кодирования (закодировать русский текст с помощью азбуки Морзе), так и декодирования (расшифровать текст, закодированный с помощью азбуки Морзе).
Выполнение таких заданий можно интерпретировать как работу шифровальщика, предлагая различные несложные ключи шифрования. Например, буквенно-цифровой, заменяя каждую букву ее порядковым номером в алфавите. Кроме того, для полноценного кодирования текста в алфавит следует внести знаки препинания и другие символы. Предложите ученикам придумать способ для отличия строчных букв от прописных.
При выполнении таких заданий следует обратить внимание учеников на то, что необходим разделительный символ — пробел, поскольку код оказывается неравномерным: какие-то буквы шифруются одной цифрой, какие-то — двумя.
Предложите ученикам подумать о том, как можно обойтись без разделения букв в коде. Эти размышления должны привести к идее равномерного кода, в котором каждый символ кодируется двумя десятичными цифрами: А — 01, Б — 02 и т.д.
Подборки задач на кодирование и шифрование информации имеются в ряде учебных пособий для школы [4].
В базовом курсе информатики для основной школы тема кодирования в большей степени связывается с темой представления в компьютере различных типов данных: чисел, текстов, изображения, звука (см. “Информационные технологии” ).
В старших классах в содержании общеобразовательного или элективного курса могут быть подробнее затронуты вопросы, связанные с теорией кодирования, разработанной К.Шенноном в рамках теории информации. Здесь существует целый ряд интересных задач, понимание которых требует повышенного уровня математической и программистской подготовки учащихся. Это проблемы экономного кодирования, универсального алгоритма кодирования, кодирования с исправлением ошибок. Подробно многие из этих вопросов раскрываются в учебном пособии “Математические основы информатики” [1].
1. Андреева Е.В., Босова Л.Л., Фалина И.Н. Математические основы информатики. Элективный курс. М.: БИНОМ. Лаборатория Знаний, 2005.
2. Бешенков С.А., Ракитина Е.А. Информатика. Систематический курс. Учебник для 10-го класса. М.: Лаборатория Базовых Знаний, 2001, 57 с.
3. Винер Н. Кибернетика, или Управление и связь в животном и машине. М.: Советское радио, 1968, 201 с.
4. Информатика. Задачник-практикум в 2 т. / Под ред. И.Г. Семакина, Е.К. Хеннера. Т. 1. М.: БИНОМ. Лаборатория Знаний, 2005.
5. Кузнецов А.А., Бешенков С.А., Ракитина Е.А., Матвеева Н.В., Милохина Л.В. Непрерывный курс информатики (концепция, система модулей, типовая программа). Информатика и образование, № 1, 2005.
6. Математический энциклопедический словарь. Раздел: “Словарь школьной информатики”. М.: Советская энциклопедия, 1988.
7. Фридланд А.Я. Информатика: процессы, системы, ресурсы. М.: БИНОМ. Лаборатория Знаний, 2003.
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Кодирование и декодирование информации
Теория к заданию 5 из ЕГЭ по информатике
Информация и ее кодирование
Различные подходы к определению понятия «информация». Виды информационных процессов. Информационный аспект в деятельности человека
Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:
Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.
Основными социально значимыми свойствами информации являются:
В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.
Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.
Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).
Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.
Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.
Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.
Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.
Язык как способ представления и передачи информации
Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.
В зависимости от способа восприятия знаки делятся на:
Для долговременного хранения знаки записывают на носители информации.
Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).
По способу связи между формой и значением знаки делятся на:
Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.
Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.
Методы измерения количества информации: вероятностный и алфавитный
Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:
Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:
I = log2 32 = 5 битов.
Если N не является целой степенью 2, то число log2N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log2N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.
Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:
N = 26; N’ = 32; I = log2N’ = log2(2 5 ) = 5 битов.
Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:
Примеры решения задач
Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log2101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log2128 = 7 битов. Для 80 измерений общий информационный объем равен:
80 · 7 = 560 битов = 70 байтов.
Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
$N$ — количество возможных событий;
Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Единицы измерения количества информации
Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).
Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.
В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.
Производные единицы измерения количества информации:
1 килобайт (Кб) = 1024 байта = 2 10 байтов
1 мегабайт (Мб) = 1024 килобайта = 2 20 байтов
1 гигабайт (Гб) = 1024 мегабайта = 2 30 байтов
1 терабайт (Тб) = 1024 гигабайта = 2 40 байтов
Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче
Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.
В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.
Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).
Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.
Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.
Примеры решения задач
Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.
Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 01002 = В416.
Скорость передачи информации и пропускная способность канала связи
Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.
Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.
Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.
Примеры решения задач
Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.
Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:
Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2 8 ⋅ 10 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = (2 8 ⋅ 125 ⋅ 2 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = 125 ⋅ 45 = 5625 Кбайт.
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$a$ — цифры численной записи, соответствующие разрядам;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 1310;
17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
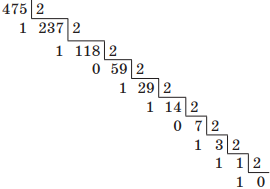
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –2 31 = –214748364810.
Максимальное положительное число равно
А = 2 31 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Формат с плавающей запятой
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
Число в экспоненциальном формате представляется в таком виде:
$q$ — основание системы счисления;
Например, десятичное число 2674,381 в экспоненциальной форме запишется так:
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.
Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.
Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 11111112 = 12710. Так как числа представляются в двоичной системе счисления, то
Аналогично, максимальное значение мантиссы равно
Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы
Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.
Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.
Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2 I = 2 8 = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:
Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.
В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2 16 = 65536 ). Коды символов могут принимать значение от 0 до 65535.
Примеры решения задач
Пример. С помощью кодировки Unicode закодирована следующая фраза:
Я хочу поступить в университет!
Оценить информационный объем этой фразы.
Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.