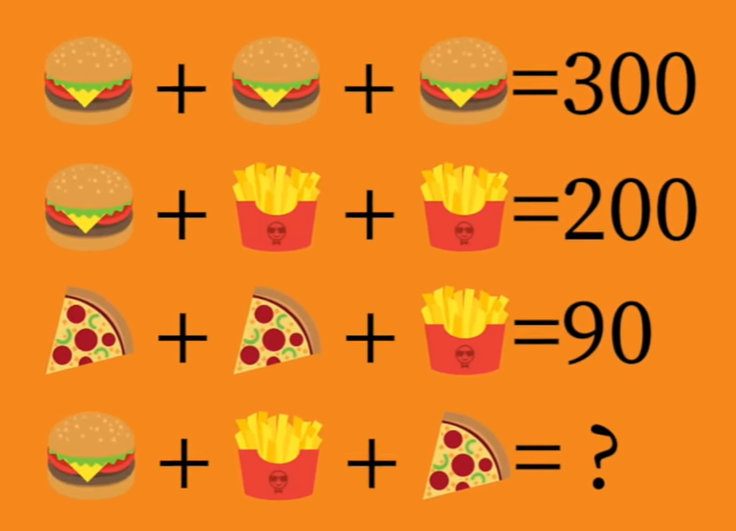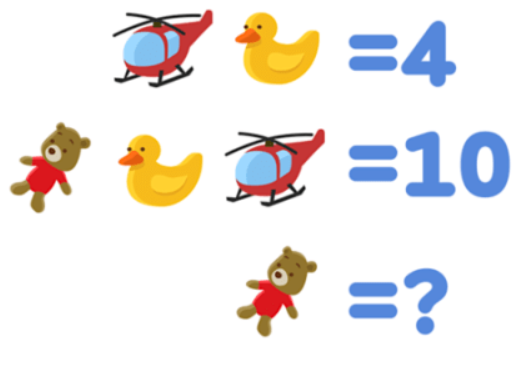задачи для решения в уме
Время размять мозги: решаем задачи на логику
В детстве в учебниках по математике всегда были задачи, помеченные звездочкой, так называемые «задачи повышенной сложности». Некоторые учителя по какой-то причине их либо пропускали, либо уделяли очень мало внимания, либо оставляли на самостоятельный разбор в качестве домашнего задания, либо просто не располагали временем для их разбора. На самом деле эти задачи активно развивают мышление ребенка, его интеллектуальные способности, в особенности логику.
«Зачем вообще развивать логику?» – спросите вы. К примеру, человек работает бухгалтером или филологом, биологом или тренером в спортивном зале. Вот, к чему в его практике акцентировать внимание на логическом мышлении? Ответ прост: развитая логика означает развитое мышление, способность видеть очевидные вещи, приходить к ним самостоятельно, а не с чьей-то помощью, делать практические выводы, которые помогают в обыденных ситуациях. Иногда логически поразмыслив, мы приходим к, казалось бы, простым и очевидным вещам, хотя до этого их не замечаем.
Кстати, развитие логического мышления, а также других навыков поможет вам учиться быстрее, эффективнее и интереснее. Этот же результат вы получите по прохождении нашей 5-недельной онлайн-программы «Лучшие техники самообразования».
Хорошо. Допустим, момент с задачками со звездочкой упущен, не вернешь былые школьные годы. Означает ли это, что нам уже никак не получится развить логику, действительно ли поезд с интеллектуальным капиталом ушел? Однозначно нет! И в этой статье мы попытаемся потренировать нашу логику. Так что включайтесь в работу и айда решать задачки на развитие логического мышления.
Ниже вы увидите ряд заданий. Не торопитесь открывать окошко с ответом, подумайте над решением, попытайтесь подойти к решению нестандартно, рассмотрите возможные варианты, перенесите смысловые акценты в задании, в общем, постарайтесь мыслить с разнопланово. В любом случае, не отчаивайтесь, если не придете к правильному ответу. Терпение и труд все перетрут. А мы желаем вам успехов!
Задача №1
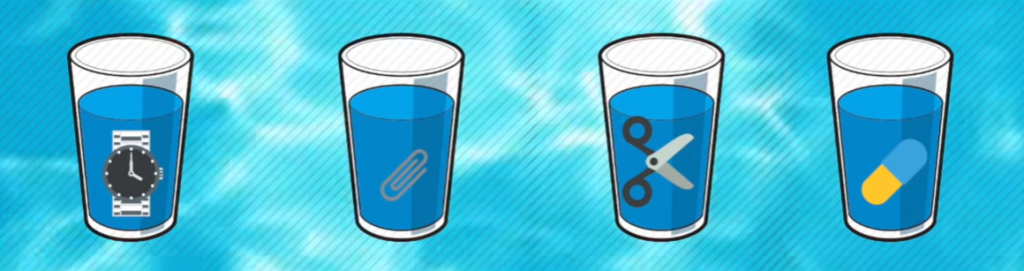
Представьте, перед вами четыре стакана, наполненных водой. В каждом стакане находятся предметы. Так:
При этом уровень воды во всех стаканах одинаковый. Визуально это выглядит следующим образом:
Вопрос: в каком стакане воды больше, чем в остальных?
Во втором стакане. Все дело в скрепке, которая по сравнению с другими предметами имеет меньший объём. Соответственно, для необходимого уровня воды требуется больше.
Размялись? Согласитесь, это было несложно. Продолжаем…
Задача №2
Давайте немного вспомним арифметические действия и применим их к задаче.
В кафе быстрого питания зашли четыре посетителя. При этом:
Схематично эту ситуацию можно представить так:
Вопрос: сколько заплатил четвертый посетитель?
Если три бургера составили 300 рублей, то один бургер стоит 100 рублей (300/3). Если второй посетитель заплатил 100 рублей за бургер, то еще 100 рублей приходится на две порции картофеля, то есть одна порция картофеля фри стоит 50 рублей (100/2). Если третий посетитель заплатил 90 рублей, потратив 50 рублей на картофель, а сорок рублей на две пиццы, то одна пицца стоит 20 рублей (40/2). Соответственно четвертый посетитель заплатил: 100 + 50 + 20 = 170 рублей.
Задача №3
Мы располагаем сковородой, на которую помещается две колеты. Нам необходимо пожарить три котлеты за 3 минуты, при том, что одна сторона котлеты жарится ровно 1 минуту (котлеты необходимо прожарить с обеих сторон).
1 минута: кладем первую и вторую котлеты, жарим с одной стороны.
2 минута: переворачиваем первую котлету; вторую (прожаренную с одной стороны) убираем и вместо нее кладем третью котлету (полностью сырую).
3 минута: убираем со сковороды первую полностью прожаренную котлету; переворачиваем третью котлету, жарим до конца и возвращаем вторую прожаренную с одной стороны котлету, её тоже жарим до готовности.
Вуаля. Котлеты поданы.
Задача №4
Предположим, у нас имеется круглый торт. Нам нужно разрезать его на восемь кусков, при этом сделав только три надреза.
Вопрос: как это сделать?
Если мы подумаем немного нестандартным путём, а именно разрежем торт не только вертикально, как мы привыкли, но и горизонтально, то получится то, что нужно. Итак, мы совершаем два надреза – крест-накрест. Получается четыре куска. Затем режем торт горизонтально посередине. В таком случае каждый кусок из уже имеющихся четырех станет вдвое ниже (или тоньше). Вот такая нехитрая технология.
Задача №5
Царь решил проверить своих троих мудрецов на мудрость, пригласил их и сказал: «Мудрецы, у меня есть 5 колпаков – 3 из них черные, а 2 белые. Сейчас вы закроете глаза, и я надену на ваши головы эти колпаки, при этом вы не будете знать, колпак какого цвета у вас на голове, но будете видеть колпаки других мудрецов». После осуществленных действий мудрецы открыли глаза и долго-долго молчали. Затем один из мудрецов произнес: «На моей голове черный колпак!» И он был прав.
Вопрос: как мудрец догадался?
После того, как мудрецы открыли глаза, они долго-долго молчали, что является ключевой фразой, потому что если бы один из мудрецов увидел на двух других белые колпаки, то он бы сразу понял, что на нем черный колпак. Поэтому первый важный вывод: на головах мудрецов нет двух белых колпаков. Соответственно, есть либо один белый, либо вообще нет.
Далее. Наши мудрецы: А, Б и В. Догадался о том, что на нем черный колпак мудрец А. Проследим ход его мыслей:
«Предположим на мне белый колпак, тогда мудрец Б, глядя на меня рассуждал бы так: «Возможно, на мне белый колпак, получается на мудреце А тоже белый колпак, тогда мудрец В сразу же сказал бы, что на нем черный колпак, но этого не происходит, значит на мне черный колпак», но ведь он не говорит, что на нем черный колпак! Значит, мое предположение неверно, и он не видит на мне белого колпака. Значит мой колпак черный!»
Да, такая вот интересная задача.
Помимо задач хотелось бы предложить загадки с подвохом. По возможности уделите время их решению, это будет увлекательно.
Загадка 1
Изначально в аквариуме плавает 10 рыбок. Однако спустя неделю 2 из них утонули, 4 – уплыли, а еще 3 – погибли. Сколько рыбок осталось в аквариуме?
10. Ни одна рыбка не покинула аквариума.
Загадка 2
Что проходит по полям и городам, но остается неподвижным?
Загадка 3
Возраст матери и дочери вместе составляет 77 лет. При этом возраст одной можно получить, если поменять цифры возраста другой. Сколько лет матери и сколько лет дочери?
Здесь возможно несколько вариантов ответа.
70 и 7; 61 и 16; 52 и 25. (Вариант 43 и 34 уже сложно представим).
Загадка 4
Перечислите 5 дней подряд, не пользуясь числами или названиями дней недели.
Загадка 5
Все пять сестер чем-то заняты:
Вопрос: Чем занята Наташа?
Помимо задачек для взрослых хотелось бы предложить задачи на логику для детей, ведь важно развивать логические мышление уже на ранних стадиях. Поэтому зовите своих детей, сестер, братьев и племянников младшего возраста, устраивайтесь поудобнее и начинайте думать.
Задача 1
Профессор всегда мечтал о домашнем животном, и он решил изобрести механических хомячков:
Хомячки, как видно, разного окраса: черный, рыжий и пятнистый. Профессор дал им имена: Уголёк, Рыжик и Пятнышко. Но цвет и имя не совпадают.
Вопрос: Как зовут хомячков, если самого темного зовут Пятнышко?
Задача 2
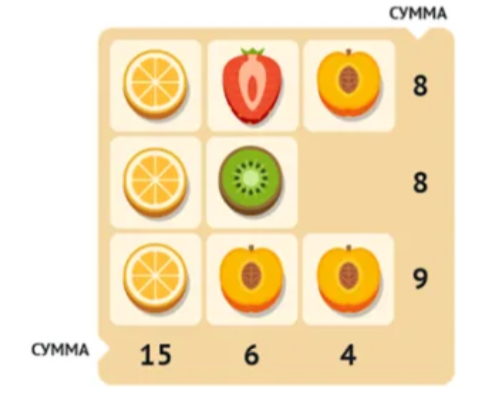
Сумма фруктов по вертикали и по горизонтали представлена на картинке:
Вопрос: сколько стоит клубника?
Задача 3
Каждой из четырёх девочек подарили одну куклу:
У Ани и Маши куклы с голубыми волосами, а у Оли и Даши – с желтыми. У Маши и Даши куклы в платьях, а у Ани и Оли – в блузках с юбками.
Вопрос: кому принадлежит какая кукла?
Задача 4
Давайте обратимся к примерам:
Вопрос: сколько стоит мишка?
Задача 5
Вновь обратимся к рисунку и посмотрим, что говорят Правдиш и Вруниш:
Правдиш всегда говорит правду.
Правдиш смотрит на пирамиду сбоку, а Вруниш – сверху.
Правдиш говорит, что нижнее кольцо красного цвета.
Вруниш говорит, что видит все кольца.
Вопрос: на какую пирамиду смотрят Правдиш и Вруниш?
Задача 6
Люда собирается на вечеринку. Она смотрит на свой гардероб:
Люда располагает четырьмя платьями и тремя парами туфель. Сколько вариантов наряда есть у Люды?
На этом мы заканчиваем наши задачки. Если вам понравилось решать подобные задания, обратите внимание на это видео:
Тут приводятся десять загадок, которые помогут поработать над логикой.
Помните, что логическое мышление имеет большое значение при принятии жизненных решений. Поэтому не ленитесь – проводите свое время за решением нескучных и полезных задачек.
5 логико-математических задач, которые поставят в тупик
Авторизуйтесь
5 логико-математических задач, которые поставят в тупик
А давайте отвлечёмся от кода и перещёлкаем 5 логико-математических задач. Попробуйте решить их в уме и напишите свои ответы в комментариях.
1. Возраст мальчика
Обилечивая человека, кондуктор поинтересовался, сколько лет его сыну. Человек ответил уклончиво:
– Моя дочь в пять раз младше моего сына, а моя жена — в 5 раз его старше. Я, в свою очередь, вдвое старше своей жены. Моя мама сегодня отмечает день рождения — ей исполнился 81 год — столько, сколько мне, жене, дочери и сыну вместе взятым.
Так сколько же лет мальчику?
Получается, что дочери один год, тогда мальчику 1 * 5 = 5 лет.
2. Вёдра с водой
Стоит два ведра ёмкостью 5 л и 9 л. Из реки необходимо набрать 3 литра воды. Как это сделать, если в распоряжении есть только эти два ведра?
Сначала заполним водой из реки девятилитровое ведро, и выльем из него воду в пятилитровое. Выходит, что в девятилитровом останется 4 литра. Выливаем всё из пятилитрового обратно в реку и переливаем в него из девятилитрового оставшиеся 4 литра. Снова наполняем водой из реки девятилитровое ведро и доливаем в меньшее литр воды. Итого в большом ведре остаётся 8 литров. Из меньшего выливаем всю воду обратно в реку и переливаем из девятилитрового в пятилитровое 5 л, после чего в большом ведре останется как раз 3 л воды.
3. Лампочки и переключатели
Есть две комнаты с низкими потолками. В первой висит три лампы накаливания, а в другой установлено три переключателя. Можно сколько угодно раз щёлкать переключатели, но в комнату с лампочками разрешено перейти только один раз.
Как узнать, к какому переключателю подсоединена каждая из лампочек?
В условии сказано, что комнаты с низкими потолками, а перед нами лампы накаливания — то есть они нагреваются. Нам достаточно включить любую из них на некоторое время, затем выключить её и включить любую другую. После этого переходим в комнату с лампочками:
4. Время по верёвкам
А как насчёт такой логико-математической задачи? Предположим, у нас есть две верёвки и бесконечное множество спичек. Каждая из этих верёвок сгорает за один час. Но вот беда — горят они неравномерно, поэтому невозможно узнать наверняка, за какое время сгорит какая-то часть веревки.
Можно ли отмерить этими двумя верёвками 45 минут, и если да, то как это сделать?
Отмерить можно. Пусть верёвки и горят неравномерно, но сгорают они точно за 1 час. В этом случае можно:
5. Баночки с таблетками
Есть двадцать баночек с таблетками. Почти во всех таблетки весят по 1 г, и только в одной — по 1,1 г. У нас есть точные кухонные весы, с помощью которых нужно определить баночку, каждая таблетка которой весит 1,1 г. Как это сделать, если можно взвесить только 1 раз?
Представим, что у нас 2 баночки, в одной из которых таблетки более тяжёлые. Даже если мы поставим их обе на весы, мы ничего не узнаем. Но если мы достанем из одной баночки одну таблетку, а также одну таблетку из другой, и положим их на весы — вот тогда-то и откроется истина. В данном случае вес будет 2,1 г или 2 г (в зависимости от того, какие по весу таблетки мы взяли). Так и определяем нашу баночку.
Вернёмся к задаче. Из каждой баночки нужно доставать разное количество таблеток. То есть из первой баночки 1 таблетку, из второй — 2, из третьей — 3 и так далее. Если бы каждая таблетка весила по 1 г, общий вес составил бы 210 г. Но поскольку в одной из баночек таблетки тяжелее, вес будет больше. Для определения нужной баночки просто воспользуемся формулой:
Понравилось решать логико-математические задачи? Тогда вас могут заинтересовать хитрые задания на логику с собеседований.
Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.
Перейти к регистрации
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
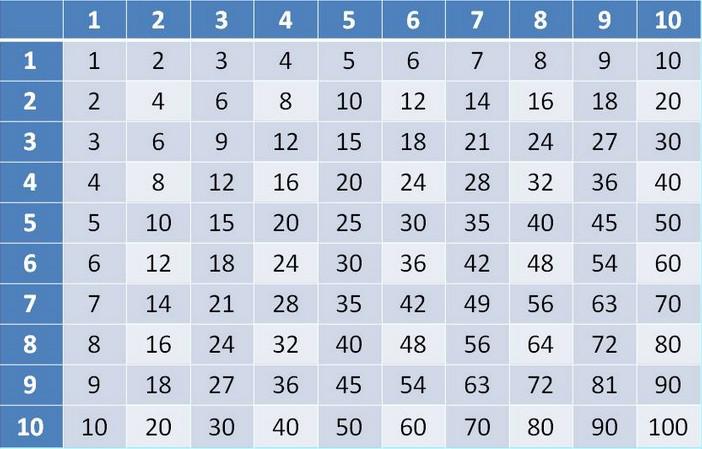
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.