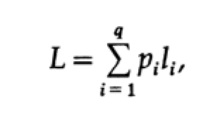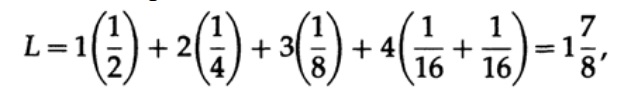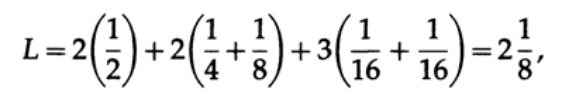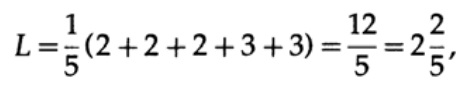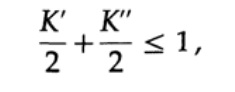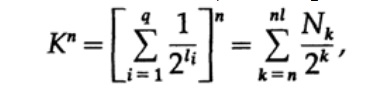заметки по теории кодирования
Описание файла
Просмотр PDF-файла онлайн
Текст из PDF
А. Ромащенко, А. Румянцев, А. ШеньЗаметки по теории кодированияМоскваИздательство МЦНМО, 2011ББК 22.1Р47Р47Ромащенко А. Е., Румянцев А. Ю., Шень А.Заметки по теории кодирования. | М.: МЦНМО, 2011. | 80 с.ISBN 978-5-94057-750-8В этих заметках, написанных по материалам лекций М.
Судана в Массачусетском технологическом институте (с его любезного разрешения), излагаются базовыерезультаты теории кодирования, а также некоторые более новые её достижения,представляющие интерес для computer science. Книга рассчитана на математиков ипрограммистов (начиная со студентов младших курсов), впервые знакомящихся стеорией кодирования.ББК 22.1Оригинал-макет предоставлен авторами.Книга является свободно распространяемой; электронная версиядоступна по адресуftp://ftp.mccme.ru/users/shen/coding.zip (исходные тексты) иftp://ftp.mccme.ru/users/shen/coding.pdf (файл книги)Андрей Евгеньевич РомащенкоАндрей Юрьевич РумянцевАлександр ШеньЗаметки по теории кодированияРедакторы И. П.
Разенштейн, В. В. ШуваловПодписано в печать 31.03.2011 г. Формат 60 × 90 1/16. Бумага офсетная.Печать офсетная. Гарнитура тип таймс. Печ. л. 5. Тираж 1000 экз. Заказ ЂИздательство Московского центра непрерывного математического образования119002, Москва, Большой Власьевский пер., 11. Тел. (499) 241-74-83.Отпечатано с готовых диапозитивов в ООО «Красногорская типография».143400, Московская область, г.
Этотпростейший код позволяет исправлять одну ошибку. (А для исправлениядвух ошибок достаточно повторять каждую букву пять раз.)Придумывая код (способы кодирования и декодирования), мы хотимсразу многого:∙ чтобы код позволял исправлять возможно большее число ошибок;∙ чтобы избыточность кода (насколько длиннее ) была бы поменьше;∙ наконец, чтобы кодирование и декодирование выполнялись бы простыми алгоритмами.Эти требования к коду во многом противоречат друг другу, и различные варианты компромисса между ними и составляют предмет теории4Предисловиекодирования.
(Отметим сразу же, что повторение символов, о которомшла речь | далеко не наилучший способ!)Вопрос о том, при каких сочетаниях параметров (избыточность и число исправляемых ошибок) такое возможно, до сих пор остаётся открытым, хотя придумано множество различных кодов, часто с использованием сложной математической техники (например, алгебраической геометрии). Вместе с тем многие важные результаты можно изложить, ограничиваясь лишь начальными сведениями из алгебры (многочлены и поля,векторные пространства над полем из двух элементов). Такое изложениеи составляет предмет этой книжки, предназначенной для первого знакомства (будущих) программистов и математиков с основными результатамитеории кодирования.
Рассказывали на семинаре в основном А. Ромащенко и А. Румянцев, текст подготовил к печатиА. Шень.Мы благодарны Мадху Судану за любезное разрешение использоватьего материалы при подготовке текста, и предупреждаем, что возможныеошибки в этом пересказе целиком на нашей совести. Мы благодарим также Григория Кабатянского и Сергея Еханина, которые посмотрели этоттекст и указали на некоторые (ныне исправленные) ошибки.А. Ромащенко, А. Румянцев, А. Шень51.
(Очевидно, числоэлементов в шаре не зависит от того, какой у него центр.)В самом деле, если код существует, то шаров с центрами в кодовыхсловах помещаются в пространстве из элементов без пересечений.Логарифмируя, можно переписать это неравенство (которое называюттакже оценкой Хэмминга или границей Хэмминга ) в таком виде: + log (, ) 6 1.Первое слагаемое можно назвать «коэффициентом полезного действия»кода: оно представляет собой отношение длины передаваемой информации к общей длине кода.
(В литературе его часто называют «скоростьюкода»).В англоязычной литературе границу Хэмминга часто называют volumebound (volume | объём).72. âÁÚÏ×ÙÅ ÏÃÅÎËÉГраница ГилбертаЕсли( − 1) (2, )
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Ричард Хэмминг: Глава 10. Теория кодирования — I
«Цель этого курса — подготовить вас к вашему техническому будущему.»

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 28 (из 30) глав. И ведем работу над изданием «в бумаге».
Теория кодирования — I
Рассмотрев компьютеры и принцип их работы, сейчас мы будем рассматривать вопрос представления информации: как компьютеры представляют информацию, которую мы хотим обработать. Значение любого символа может зависит от способа его обработки, у машины нет никакого определенного смысла у используемого бита. При обсуждении истории программного обеспечения 4 главе мы рассматривали некоторый синтетический язык программирования, в нём код инструкции останова совпадал с кодом других инструкций. Такая ситуация типична для большинства языков, смысл инструкции определяется соответствующей программой.
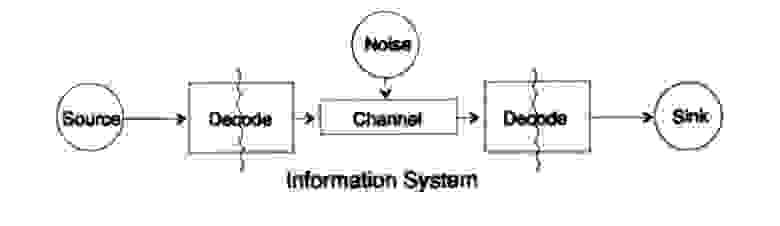
Для упрощения проблемы представления информации рассмотрим проблему передачи информации от точки к точке. Этот вопрос связан с вопросом сохранения информация. Проблемы передачи информации во времени и в пространстве идентичны. На рисунке 10.1 представлена стандартная модель передачи информации.
Рисунок 10.1
Слева на рисунке 10.1 находится источник информации. При рассмотрении модели нам неважна природа источника. Это может быть набор символов алфавита, чисел, математических формул, музыкальных нот, символов, которыми мы можем представить танцевальные движения — природа источника и значение хранящихся в нём символов не является частью модели передачи. Мы рассматриваем только источник информации, с таким ограничением получается мощная, общая теория, которую можно распространить на многие области. Она является абстракцией из многих приложений.
Когда в конце 1940 годов Шеннон создал теорию информации, считалось, что она должна была называться теорией связи, но он настоял на термине информация. Этот термин стал постоянной причиной как повышенного интереса, так и постоянных разочарований в теории. Следователи хотели строить целые «теории информации», они вырождались в теории о наборе символов. Возвращаясь к модели передачи, у нас есть источник данных, которые необходимо закодировать для передачи.
Кодер состоит из двух частей, первая часть называется кодер источника, точное название зависит от типа источника. Источникам разных типов данных соответствуют разные типы кодеров.
Вторая часть процесса кодирования называется кодирование канала и зависит от вида канала для передачи данных. Таким образом, вторая часть процесса кодирования согласована с типом канала передачи. Таким образом, при использовании стандартных интерфейсов данные из источника в начале кодируются согласно требованиям интерфейса, а потом согласно требованиям используемого канала передачи данных.
Согласно модели, на рисунке 10.1 канал передачи данных подвергается воздействию «дополнительного случайного шума». Весь шум в системе объединен в этой точке. Предполагается, что кодер принимает все символы без искажений, а декодер выполняет свою функцию без ошибок. Это некоторая идеализация, но для многих практических целей она близка к реальности.
Фаза декодирования также состоит из двух этапов: канал — стандарт, стандарт- приемник данных. В конце передачи данных передаются потребителю. И снова мы не рассматриваем вопрос, как потребитель трактует эти данные.
Как было отмечено ранее, система передачи данных, например, телефонных сообщений, радио, ТВ программ, представляет данные в виде набора чисел в регистрах вычислительной машины. Повторю снова, передача в пространстве не отличается от передачи во времени или сохранения информации. Есть ли у вас есть информация, которая потребуется через некоторое время, то ее необходимо закодировать и сохранить на источнике хранения данных. При необходимости информация декодируется. Если система кодирования и декодирования одинаковая, мы передаем данные через канал передачи без изменений.
Фундаментальная разница между представленной теорией и обычной теорией в физике — это предположение об отсутствии шума в источнике и приемнике. На самом деле, ошибки возникают в любом оборудовании. В квантовой механике шум возникает на любых этапах согласно принципу неопределённости, а не в качестве начального условия; в любом случае, понятие шума в теории информации не эквивалентно аналогичному понятию в квантовой механике.
Для определенности будем далее рассматривать бинарную форму представления данных в системе. Другие формы обрабатываются похожим образом, для упрощения не будем их рассматривать.
Начнем рассмотрение систем с закодированными символами переменной длины, как в классическом коде Морзе из точек и тире, в котором часто встречающиеся символы — короткие, а редкие — длинные. Такой подход позволяет достичь высокой эффективности кода, но стоит отметить, что код Морзе — тернарный, а не бинарный, так как в нём присутствует символ пробела между точками и тире. Если все символы в коде одинаковой длины, то такой код называется блочным.
Первое очевидное необходимое свойство кода — возможность однозначно декодировать сообщение при отсутствии шума, по крайней мере, это кажется желаемым свойством, хотя в некоторых ситуациях этим требованием можно пренебречь. Данные из канала передачи для приемника выглядят как поток символов из нулей и единичек.
Будем называть два смежных символа двойным расширением, три смежных символ тройным расширением, и в общем случае если мы пересылаем N символов приемник видит дополнения к базовому коду из N символов. Приемник, не зная значение N, должен разделить поток в транслируемые блоки. Или, другими словами, у приемника должна быть возможность выполнить декомпозицию потока единственным образом для того, чтобы восстановить исходное сообщение.
Рассмотрим алфавит из небольшого числа символов, обычно алфавиты намного больше. Алфавиты языков начинается от 16 до 36 символов, включая символы в верхнем и нижнем регистре, числа знаки, препинания. Например, в таблице ASCII 128 = 2^7 символов.
Рассмотрим специальный код, состоящий из 4 символов s1, s2, s3, s4
s1 = 0; s2 = 00; s3 = 01; s4 = 11.
Как приёмник должен трактовать следующее полученное выражение
Как s1s1s4 или как s2s4?
Вы не можете однозначно дать ответ на этот вопрос, этот код однозначно нет декодируется, следовательно, он неудовлетворительный. С другой стороны, код
s1 = 0; s2 = 10; s3 = 110; s4 = 111
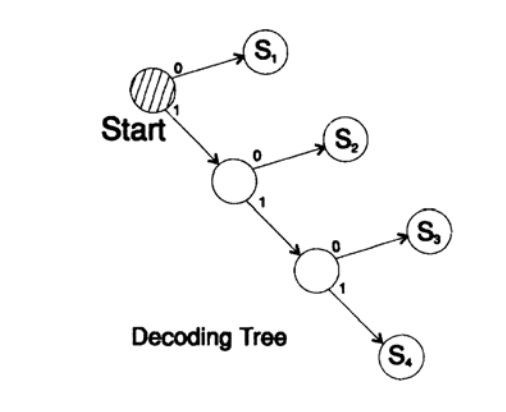
декодирует сообщение уникальным способом. Возьмем произвольную строку и рассмотрим, как ее будет декодировать приемник. Вам необходимо построить дерево декодирования Согласно форме на рисунке 10.II. Строка
может быть разбита на блоки символов
110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110,…
согласно следующему правилу построения дерева декодирования:
Если вы находитесь в вершине дерева, то считываете следующий символ. Когда вы достигаете листа дерева, вы преобразовывает последовательность в символ и возвращайтесь назад на старт.
Причина существования такого дерева в том, что ни один символ не является префиксом другого, поэтому вы всегда знаете, когда необходимо вернуться в начало дерево декодирования.
Необходимо обратить внимание на следующее. Во-первых, декодирование строго поточный процесс, при котором каждый бит исследуется только однажды. Во-вторых, в протоколах обычно включаются символы, которые являются маркером окончания процесса декодирования и необходимы для обозначения конца сообщения.
Отказ от использования завершающего символа является частой ошибкой при дизайне кодов. Конечно же можно предусмотреть режим постоянного декодирования, в этом случае завершающая символ не нужен.
Следующий вопрос — это коды для поточного (мгновенного) декодирования. Рассмотрим код, который получается из предыдущего отображением символов
s1 = 0; s2 = 01; s3 = 011; s4 = 111.
Предположим мы получили последовательность 011111. 111. Единственный способ, которым можно декодировать текст сообщения: группировать биты с конца по 3 в группе и выделять группы с ведущим нулем перед единичками, после этого можно декодировать. Такой код декодируемый единственным способом, но не мгновенным! Для декодирования необходимо дождаться окончания передачи! В практике такой подход нивелирует скорость декодирования (теорема Макмиллана), следовательно, необходимо поискать способы мгновенного декодирования.
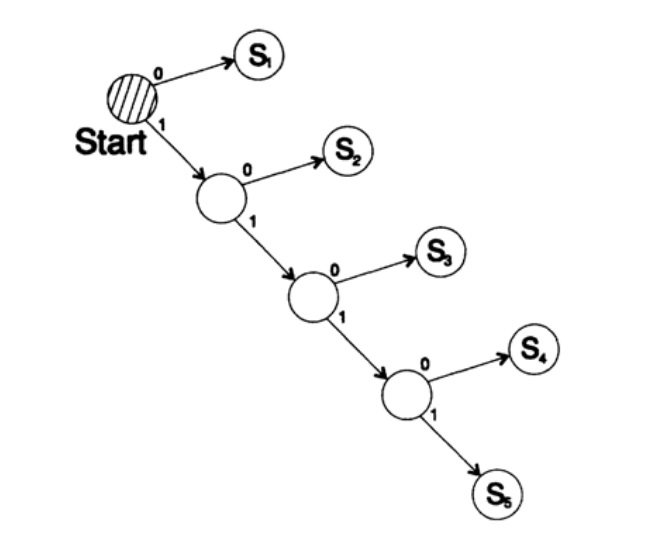
Рассмотрим два способа кодирования одного и того же символа, Si:
s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,
Дерево декодирование этого способа представлено на рисунке 10.III.
s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111,
Дерево декодирование это ухода представлены на рисунке 10.IV.
Наиболее очевидным способом измерения качество кода — это средняя длина для некоторого набора сообщений. Для этого необходимо вычислить длину кода каждого символа, помноженную на соответствующую вероятность появления pi. Таким образом получится длина всего кода. Формула средней длины L кода для алфавита из q символов выглядит следующим образом
где pi — вероятность появления символа si, li — соответствующая длина закодированного символа. Для эффективного кода значение L должно быть как можно меньше. Если P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 и p5 = 1/16, тогда для кода #1 получаем значение длины кода
Полученные значения говорят о предпочтительности первого кода.
Если у всех слов в алфавите будет одинаковая вероятность возникновения, тогда более предпочтительным будет второй код. Например, при pi = 1/5 длина кода #1
этот результат показывает предпочтительность 2 кода. Таким образом, при разработке «хорошего» кода необходимо учитывать вероятность возникновения символов.
Рассмотрим неравенство Крафта, которое определяет предельное значение длины кода символа li. По базису 2 неравенство представляется в виде
Это неравенство говорит о том, что в алфавите не может быть слишком много коротких символов, в противном случае сумма будет довольно большой.
Рассмотрим доказательство теорема Макмиллана. Применим неравенство Крафта к непоточно декодируем кодам. Доказательство построено на том факте, что для любого числа K > 1 n-ая степень числа заведомо больше линейной функции от n, где n — довольно большое число. Возведем неравенство Крафта в n-ую степень и представим выражение в виде суммы
где Nk число символов длины k, суммирование начинаем с минимальной длины n-го представление символа и заканчиваем максимальной длины nl, где l — максимальная длина закодированного символа. Из требования уникального декодирования следует, что. Сумма представляется в виде
Если K > 1, тогда необходимо n установить довольно большим для того, чтобы неравенство стало ложным. Следовательно, k Содержание книги и переведенные главы
НИС Методы и алгоритмы защиты информации
Содержание
О семинаре
Цель семинара – познакомить участников с основными понятиями, методами и алгоритмами криптографии и теории кодирования. Параллельно мы обсуждаем необходимые сведения из алгебры, теории чисел и дискретной математики. Семинар проходит в форме докладов участников с их последующим обсуждением. Участие в семинаре позволит освоить современные методы защиты и передачи информации. Также будут даны многочисленные примеры практического использования материала, излагаемого в базовых математических курсах.
Семинар проводится для студентов 2 курса в 1-3 модулях.
Преподаватель
Учебные ассистенты
Полезные ссылки
План семинара
Криптография
| № | Тема доклада | Литература | Отвечающий доклад | Дата выступления | Отметка о выполнении | Дедлайн ДЗ | Отметка о проверке |
|---|---|---|---|---|---|---|---|
| 1 | Простейшие криптосистемы. Сдвиг и аффинное преобразование. Частотный анализ. Биграммы. Ключ шифрования и ключ дешифрования. Классические криптосистемы и системы с открытым ключом | К, Гл. III, пар. 1 К, Гл. IV, пар. 1 | Кунин Илья | 21.09.2021 | TBA | ||
| 2 | Необходимые факты из теории чисел: обратимость вычета по данному модулю, алгоритм нахождения обратного элемента, малая теорема Ферма, функция Эйлера и теорема Эйлера, китайская теорема об остатках, возведение в степень методом повторного возведения в квадрат | K, Гл. I | Красковский Дмитрий | 21.09.2021 | TBA | ||
| 3 | Строение конечных полей | ЛН | — | — | — | — | — |
| 4 | Квадратичные вычеты и закон взаимности | K, Гл. II, пар. 2 | Зобнин Алексей | 21.09.2021 | TBA | ||
| 5 | Необходимые сведения из алгебры: группы и подгруппы, примеры конечных групп, порядок элемента, циклические группы и их порождающие | любой учебник по алгебре | Неймышева Юлия | TBA | TBA | ||
| 6 | Криптосистема RSA | K, Гл. IV, пар. 2 П, 1.2 | Куликов Богдан | TBA | TBA | ||
| 7 | Задача дискретного логарифмирования и основанные на ней криптосистемы: система Диффи-Хеллмана обмена ключами, системы Мэсси-Омура и Эль-Гамаля. Понятие электронной подписи. Электронная подпись в RSA и по Эль-Гамалю | K, Гл. IV, пар. 1, 3 П, 1.3 В, Гл. 5 | Каменский Андрей | TBA | TBA | ||
| 8 | Проверка чисел на простоту и задача факторизации. Решето Эратосфена. Псевдопростые числа и числа Кармайкла. Метод Поклингтона. (p-1)-метод Полларда. | K, Гл. V П, 2.4 В, Гл. 1-2 | Абаев Фёдор | TBA | TBA | ||
| 9 | Задача о рюкзаке как задача комбинаторной оптимизации. Быстрорастущие наборы. Рюкзачная криптосистема | K, Гл. IV, пар. 4 | Соколов Александр | TBA | TBA | ||
| 10 | Протоколы с нулевым разглашением. Три примера: раскраска карты в три цвета, поиск гамильтонова пути и извлечение корня в кольце вычетов | K, Гл. IV, пар. 5 | Гайсин Ислам | TBA | TBA | ||
| 11 | Математика разделенного секрета. Пороговые (n,k)-схемы доступа. Схема Шамира и схема Блэкли. Связь с теорией матроидов | Я, Гл. 5 | Коннов Илья | TBA | TBA | ||
| 12 | Математика эллиптических кривых: групповой закон, формулы сложения и удвоения точек, теорема Хассе о числе точек на эллиптической кривой | K, Гл. VI, пар. 1 П, гл. 4 | Капустин Егор | TBA | TBA | ||
| 13 | Нахождение точки на эллиптической кривой. Задача дискретного логарифмирования. Криптосистемы на эллиптических кривых: аналоги систем Диффи-Хеллмана и Эль-Гамаля | K, Гл. VI, пар. 2 | Верзаков Ефим | TBA | TBA | ||
| 14 | Проверка чисел на простоту и разложение на множители при помощи эллиптических кривых. Аналог метода Поклингтона и метод Ленстры | K, Гл. VI, пар. 3-4 В, Гл. 4 | Порохнин Даниил | TBA | TBA |
Теория кодирования
Литература
Оценивание
Участие в семинаре без доклада
Участие в семинаре с одним докладом по одной из частей семинара (или по криптографии, или по теории кодирования)
K = 0,2 КП + 0,2 АУ + 0,3 ДП + 0,3 ИК
Участие в семинаре с двумя докладами по обеим частям семинара (и по криптографии, и по теории кодирования)
K = 0,2 КП + 0,2 АУ + 0,3 ДП1 + 0,3 ДП2
А. Ромащенко, А. Румянцев, А. Шень
Заметки по теории кодирования
Издательство МЦНМО, 2011
Ромащенко А. Е., Румянцев А. Ю., Шень А.
Р47 Заметки по теории кодирования. | М.: МЦНМО, 2011. | 80 с.
В этих заметках, написанных по материалам лекций М. Судана в Массачусетском технологическом институте (с его любезного разрешения), излагаются базовые результаты теории кодирования, а также некоторые более новые её достижения, представляющие интерес для computer science. Книга рассчитана на математиков и программистов (начиная со студентов младших курсов), впервые знакомящихся с теорией кодирования.
ББК 22.1 Оригинал-макет предоставлен авторами.
Книга является свободно распространяемой; электронная версия доступна по адресу ftp://ftp.mccme.ru/users/shen/coding.zip (исходные тексты) и ftp://ftp.mccme.ru/users/shen/coding.pdf (файл книги) Андрей Евгеньевич Ромащенко Андрей Юрьевич Румянцев Александр Шень Заметки по теории кодирования Редакторы И. П. Разенштейн, В. В. Шувалов Подписано в печать 31.03.2011 г. Формат 60 90 1 16. Бумага офсетная.
/ Печать офсетная. Гарнитура тип таймс. Печ. л. 5. Тираж 1000 экз. Заказ Ђ Издательство Московского центра непрерывного математического образования 119002, Москва, Большой Власьевский пер., 11. Тел. (499) 241-74-83.
Отпечатано с готовых диапозитивов в ООО «Красногорская типография».
143400, Московская область, г. Красногорск, Коммунальный квартал, д. 2.
c Ромащенко А. Е., Румянцев А. Ю., Шень А., 2011.
ISBN 978-5-94057-750- Предисловие Слово «кодирование» в названии этой книжки не означает шифрования (сохранения сообщения в секрете) | этим занимается не теория кодирования, а криптография, которой мы не касаемся); не идёт речь также о теоретических и практических проблемах перехода от одной кодировки символов к другой. Основной вопрос теории кодирования | как записать сообщение в такой форме, чтобы искажение некоторой части записи (например, при передаче данных) не помешало восстановлению сообщения в исходной форме.
декодер = ( ) кодер = () канал связи Имеется в виду, что исходное сообщение (последовательность битов или других символов) преобразуется в некоторую другую (более длинную) последовательность. Затем передаётся по каналу связи с помехами (или хранится на ветхом носителе), превращаясь при этом в.
Наконец, из извлекается сообщение, которое должно совпадать с исходным ().
Например, мы можем повторить каждую букву сообщения три раза, получив втрое более длинное сообщение. Если одна из букв в слове испортится, это не помешает восстановить. В этом примере алгоритм кодирования (кодер) утраивает каждую букву, а алгоритм декодирования (декодер) берёт наиболее частую букву в каждой тройке. Этот простейший код позволяет исправлять одну ошибку. (А для исправления двух ошибок достаточно повторять каждую букву пять раз.) Придумывая код (способы кодирования и декодирования), мы хотим сразу многого:
чтобы код позволял исправлять возможно большее число ошибок;
чтобы избыточность кода (насколько длиннее ) была бы поменьше;
наконец, чтобы кодирование и декодирование выполнялись бы простыми алгоритмами.
Эти требования к коду во многом противоречат друг другу, и различные варианты компромисса между ними и составляют предмет теории 4 Предисловие кодирования. (Отметим сразу же, что повторение символов, о котором шла речь | далеко не наилучший способ!) Вопрос о том, при каких сочетаниях параметров (избыточность и число исправляемых ошибок) такое возможно, до сих пор остаётся открытым, хотя придумано множество различных кодов, часто с использованием сложной математической техники (например, алгебраической геометрии). Вместе с тем многие важные результаты можно изложить, ограничиваясь лишь начальными сведениями из алгебры (многочлены и поля, векторные пространства над полем из двух элементов). Такое изложение и составляет предмет этой книжки, предназначенной для первого знакомства (будущих) программистов и математиков с основными результатами теории кодирования. В неё включены также некоторые более новые результаты (декодирование списком, теорема Голдрайха < Левина, связь с экспандерами).
* * * Большая часть этих заметок была сделана участниками семинара кафедры математической логики и теории алгоритмов механико-математического факультета МГУ в 2004/5 учебном году, разбиравшими записи лекций Мадху Судана в Массачусетском технологическом институте (по выложенным в интернете на домашней странице Судана материалам, см. http://theory.csail.mit.edu/
madhu). Рассказывали на семинаре в основном А. Ромащенко и А. Румянцев, текст подготовил к печати А. Шень.
Мы благодарны Мадху Судану за любезное разрешение использовать его материалы при подготовке текста, и предупреждаем, что возможные ошибки в этом пересказе целиком на нашей совести. Мы благодарим также Григория Кабатянского и Сергея Еханина, которые посмотрели этот текст и указали на некоторые (ныне исправленные) ошибки.
1. Коды с исправлением ошибок:
постановка задачи Пусть | конечный алфавит (множество букв ). Через мы обозначаем множество всех слов (конечных последовательностей букв) длины в алфавите. Расстояние Хэмминга между двумя словами.
и. из определяется как число позиций, в которых эти слова отличаются (число тех, при которых = ).
Рассмотрим отображение : при как способ кодирования информации при её передаче. Получив на вход слово, мы передаём по каналу связи слово (). В процессе передачи некоторые символы слова () могут быть искажены. Несмотря на это, мы хотим, чтобы было возможно восстановить исходное слово. Другими словами, мы хотим, чтобы () нельзя было спутать с ( ) даже после того, как некоторые буквы в обоих словах искажены. Если разрешается искажать не более позиций (в каждом слове), то для однозначного восстановления необходимо и достаточно, чтобы расстояние между () и ( ) было 2 + 1 или больше.
Более формально, кодом называется отображение :. Значения этого отображения называются кодовыми словами. Минимальное из расстояний ( (), ( )) при = называется минимальным расстоянием кода. Код с минимальным расстоянием позволяет исправлять = ( 1)/2 ошибок, поскольку при таком шары радиуса с центрами в кодовых словах не пересекаются. (Шар радиуса с центром в слове определяется как множество всех слов, отличающихся от не более чем в позициях. Через обозначается целая часть числа, то есть наибольшее целое число, не превосходящее.) Такая «помехоустойчивость» кода возникает, как говорят, за счёт «избыточности» при передаче информации: вместо символов мы передаём символов, при этом. Чем больше и чем ближе к, тем лучше код. Конечно, эти два требования противоречат друг другу и одно достигается за счёт другого.
Задачу построения оптимального кода при данных, и можно интерпретировать геометрически: в метрическом пространстве нужно упаковать без пересечений как можно больше шаров радиуса. Другой вариант формулировки: требуется найти как можно больше точек с попарными расстояниями 2 + 1 или больше. После того как шары (их центры) выбраны, можно взять, равное целой части логарифма числа таких шаров (точек) по основанию || (число букв во входном алфавите), и произвольно сопоставить слова длины с центрами шаров. (Число выбрано максимально возможным, при котором шаров хватит.) Выбор этого соответствия (между кодируемыми словами и их кодами) безразличен, пока мы не интересуемся сложностью алгоритмов кодирования и декодирования. Алгоритм кодирования вычисляет функцию, то есть по входному слову даёт ( ). Алгоритм декодирования с исправлением ошибок получает на вход слово, отстоящее от некоторого кодового слова ( ) на расстояние не больше, и даёт на выходе.
Естественно, мы хотим, чтобы алгоритмы кодирования и декодирования были не очень сложными и работали быстро.
2. Базовые оценки При каких значениях параметров = ||. код :, исправляющий ошибок, существует, а при каких нет? Две самые простые оценки (с той и другой стороны) таковы.
Граница Хэмминга Если код с указанными параметрами существует, то Здесь через (, ) обозначается объём (число элементов) шара радиуса в пространстве слов длины в алфавите из букв. (Очевидно, число элементов в шаре не зависит от того, какой у него центр.) В самом деле, если код существует, то шаров с центрами в кодовых словах помещаются в пространстве из элементов без пересечений.
Логарифмируя, можно переписать это неравенство (которое называют также оценкой Хэмминга или границей Хэмминга) в таком виде:
Первое слагаемое можно назвать «коэффициентом полезного действия»
кода: оно представляет собой отношение длины передаваемой информации к общей длине кода. (В литературе его часто называют «скоростью кода»).
В англоязычной литературе границу Хэмминга часто называют volume bound (volume | объём).
Граница Гилберта то существует код с параметрами.
В самом деле, будем выбирать кодовые слова одно за другим произвольным образом, следя лишь за тем, чтобы расстояния между ними были больше 2. Если нового слова выбрать нельзя, это значит, что всё пространство (в котором элементов) полностью покрыто шарами, каждый из которых состоит из (2, ) элементов. Наше предположение гарантирует, что при этом имеется как минимум шаров, что и требуется.
Переходя к логарифмам, условие можно записать так:
(для простоты записи мы немного усилили условие и тем самым ослабили утверждение о существовании кода, отбросив вычитание единицы). Это неравенство называют границей Гилберта. Не следует путать автора этой оценки Эдгара Гилберта (Edgar N. Gilbert) со знаменитым математиком Давидом Гильбертом (David Hilbert).
Графики Полезно изобразить границы Хэмминга и Гилберта на одном графике. По горизонтали будем откладывать кодовое расстояние (примерно равное 2, удвоенному числу исправляемых ошибок) в долях ; по вертикали | коэффициент полезного действия кода (отношение /, где | число кодируемых символов, а | длина кода).
Ограничимся случаем = 2 и будем использовать приближённую формулу для объёма шара.
Необходимое условие существование кода, исправляющего ошибок (граница Хэмминга):
Достаточное условие существования кода с расстоянием не меньше Формулы эти похожи, но только и отличаются примерно в два раза.
Поэтому график для границы Хэмминга получается двукратным растяжением графика для границы Гилберта по горизонтали (рис. 1).
По этой картинке можно определить, скажем, что кода с коэффициентом полезного действия 1/2 и расстоянием в /3 не существует | соответствующая точка лежит выше границы Хэмминга. С другой стороны, код с коэффициентом полезного действия 1/8 и расстоянием /4 (и тем самым допускающим исправление /8 ошибок) существует | соответствующая точка лежит ниже границы Гилберта. (Всё сказанное относится к достаточно большим, так как мы пренебрегали членами порядка (log /).) Что происходит между этими границами | один из основных вопросов теории кодирования, до сих пор не решённый полностью (несмотря на множество частичных результатов).
3. Случайные коды Границу Гилберта можно достичь и другими способами. В этом разделе мы используем случайный код, а в следующем разделе | линейный.
Пусть фиксировано некоторое число. Будем выбирать кодовых слов. случайно среди равновероятных элементов. При этом мы считаем все. независимыми. (В частности, вероятность совпадения и при = отлична от нуля, хотя и мала.) Для фиксированного <1. >рассмотрим вероятность того, что в шар радиуса 2 с центром попадут другие кодовые слова. Вероятность попадания с данным равна (2, )/ (доле пространства, занимаемой шаром радиуса 2); вероятность того, что хотя бы одно (при = ) попадёт в этот шар, не больше (2, )/. Будем называть те, при которых в шар с центром в попали другие, «плохими». Тогда вероятность каждого оказаться плохим не больше (2, )/. Поэтому математическое ожидание числа плохих не больше (2, )/, а математическое ожидание доли плохих (среди всех чисел 1. ) | не больше (2, )/.
Предположим теперь, что (вдвое меньшее число кодовых слов, чем допускает граница Гилберта).
Тогда математическое ожидание доли плохих не больше 1/2.
Итак, если выбирать кодовые слова. случайно, то число плохих в среднем (усреднение по выбору случайного кода) будет меньше /2. Следовательно, среди всех возможных выборов кодовых слов существует такой, при котором эта доля не больше 1/2.
Зафиксировав один из таких вариантов и выкинув плохие кодовые слова (их не более половины), мы получим код с расстоянием не менее 2+1, который всего лишь в четыре раза хуже (по числу слов | мы начали с вдвое меньшего числа, да ещё отбросили половину), чем построенный ранее. Уменьшение количества кодовых слов в четыре раза означает, что мы уменьшаем (число битов, определяющих кодовое слов) лишь на два бита.
4. Линейные коды Если есть степень простого числа, то (как известно из алгебры) существует поле F из элементов. В этом случае можно считать, что = F, а слова образуют векторное пространство (размерности или ) над F. В этой ситуации возникает понятие линейного кода. Такой 1 Этот способ вероятностного доказательства существования часто применяется в комбинаторике: чтобы установить, что существует вариант, при котором какая-то величина велика (или мала), мы доказываем, что её среднее значение по какому-то распределению вероятностей велико (или мало). Например, вершины любого графа можно так раскрасить в два цвета, чтобы как минимум половина рёбер соединяла вершины разных цветов. В самом деле, при случайной раскраске каждое ребро оказывается «разноцветным» с вероятностью 1/2 и потому средняя доля разноцветных рёбер равна 1/2.
код представляет собой линейное (над F ) отображение F F. Это отображение задаётся матрицей размера, элементы которой принадлежат полю F.
Множество всех кодовых слов линейного кода (образ этого отображения) представляет собой подпространство в F. В силу линейности окрестности всех кодовых слов устроены одинаково (отличаются сдвигом). Поэтому минимальное расстояние линейного кода можно измерять в любой точке, в частности, в нуле: оно равно минимально возможному числу ненулевых координат в ненулевом кодовом слове.
Чтобы построить искомый линейный код, будем добавлять в базис подпространства вектор за вектором, следя за тем, чтобы кодовое расстояние оставалось больше 2. Пусть уже есть базисных векторов, которые порождают некоторое подпространство. Новый (добавляемый) базисный вектор должен быть на расстоянии более 2 от всех векторов подпространства; это, как легко понять, гарантирует, что и после его добавления расстояние между любыми двумя векторами останется больше 2. Другими словами, новый вектор должен лежать вне объединения шаров радиуса 2.
Заметим, что в случае линейного кода кодирование выполняется легко (умножение на матрицу кода), но про декодирование по-прежнему ничего хорошего сказать нельзя (хотя для некоторых линейных кодов, как мы увидим, существуют быстрые алгоритмы декодирования).
Линейное подпространство размерности в пространстве F можно задавать не только как образ линейного оператора F F, но и как ядро оператора F F, имеющего максимальный ранг ( ). Такой оператор задаётся матрицей из строк и столбцов. Векторстолбец высоты является кодовым словом тогда и только тогда, когда = 0 ( уравнений с переменными; можно сказать, что эти уравнения представляют собой «контрольные суммы», которые у кодовых слов должны равняться нулю). Эта матрица называется проверочной, поскольку умножением на неё проверяется принадлежность множеству кодовых слов. Код с проверочной матрицей имеет расстояние тогда и только тогда, когда любые 1 столбцов матрицы линейно независимы. В самом деле, кодовое слово, в котором лишь 1 позиций отличны от нуля, как раз и выражает линейную зависимость между 1 столбцами проверочной матрицы.
5. Код Хэмминга Сейчас мы рассмотрим случай, когда удаётся указать простой код с наилучшими возможными параметрами (шары плотно заполняют всё пространство, достигая границы Хэмминга). Этот код называется кодом Хэмминга и позволяет исправлять одну ошибку, то есть имеет минимальное расстояние 3.
Рассмотрим алфавит из двух букв B = <0, 1>. Мы будем рассматривать его как поле из двух элементов со сложением () и умножением по модулю 2.
В пространстве B шар радиуса 1 состоит из +1 элементов (центр и ещё слов, отличающихся от центрального в одной из позиций). Всего слов 2, поэтому шансы на укладку шаров без пробелов и перекрытий есть, лишь если 2 кратно + 1, то есть если + 1 есть степень двойки:
= 2 1 для некоторого целого (при = 3, 7, 15, 31. ; случай = 1 тривиален).
При = 3 есть 8 вершин куба, которые разбиваются на два шара с центрами в противоположных вершинах. Каждый из шаров содержит элемента, так что плотная упаковка действительно возможна.
Оказывается, что она возможна и при остальных значениях из указанной серии. Чтобы убедиться в этом, рассмотрим произвольное = 2 1 и запишем все числа от 1 до в двоичной системе по столбцам матрицы (от 1 в первом столбце до в последнем; каждое число записывается сверху вниз, так что младший разряд оказывается внизу).
Например, при = 7 получится матрица Строки этой матрицы будем рассматривать как способы вычисления контрольных сумм. (Другими словами, мы используем эту матрицу как проверочную). А именно, пусть дано произвольное слово из B. Для него мы вычислим три контрольных суммы, складывая по модулю 2 те биты, против которых в матрице стоит единица: (для первой строки), (для второй строки) и (для третьей строки).
Можно сказать, что мы умножаем матрицу на столбец с элементами (. ), получая столбец из трёх контрольных сумм.
Кодовые слова (центры шаров) | это те слова длины 7, для которых все три контрольные суммы равны нулю. Линейная алгебра говорит, что они образуют подпространство размерности 4 (три уравнения на семь переменных; легко проверить, что уравнения независимы, посмотрев на первый, второй и четвёртый столбцы), состоящее из 2 = 16 кодовых слов.
Мы описали алгоритм декодирования, исправляющий ошибку в любом (но только одном) бите. Отсюда автоматически следует, что шары не пересекаются. Тем самым у нас есть 16 шаров, каждый из которых состоит из 8 элементов, и вместе они покрывают все 128 элементов семимерного булева куба B. Точно так же для произвольных и = 2 1 строится проверочная матрица из столбцов высоты (двоичные записи чисел 1. ). Её строки указывают контрольных сумм для векторов из B. Кодовых слов 2, в каждом шаре +1 = 2 элементов и они покрывают B полностью.
Заметим, что этот код не только совершенный (всё пространство занято шарами без пробелов), но и имеет простые алгоритмы кодирования и декодирования. (Про декодирование мы уже говорили; при кодировании можно считать биты,, контрольными, а остальные значащими, и выбирать контрольные биты так, чтобы получить кодовое слово.) Единственный недостаток кода Хэмминга | что он исправляет только одну ошибку.
1. Можно вычеркнуть из матрицы часть столбцов. При этом мы получим код с тем же числом контрольных сумм, но с меньшим числом битов. Он уже не будет совершенным, но будет достаточно эффективным.
(Больше половины столбцов выкидывать нет смысла, поскольку тогда уж лучше уменьшить высоту матрицы. А если мы выбрасываем меньше половины столбцов, то теряем не больше половины места.) 2. Аналогичное построение возможно и при 2, если существует поле F из элементов (это бывает, напомним, когда есть степень простого числа). Для этого напишем в столбцах матрицы ненулевые векторы из F, причём из каждого класса пропорциональных друг другу векторов оставим только один. Всего ненулевых векторов 1, в каждом классе 1 пропорциональных друг другу векторов, так что классов (и столбцов матрицы) будет = ( 1)/( 1). Ясно, что ранг полученной матрицы равен.
Изменение одной позиции в кодовом слове изменит контрольные суммы на вектор, пропорциональный одному из столбцов матрицы, и по построению этот столбец (и тем самым номер изменённого символа) определится однозначно.
Кодовых слов будет, размер шара 1 + ( 1) (в каждой из позиций можно заменить букву на ( 1) других, да ещё центр шара), что равно Таким образом, шары заполняют всё пространство.
3. Для доказательства того, что код Хэмминга имеет расстояние не меньше 3, достаточно было бы сослаться на то, что любые две строки в нашей матрице (=любые два столбца в проверочной матрице из предыдущего раздела) линейно независимы. Но нам важен и простой алгоритм декодирования.
Рис. 2. Для двухбуквенного алфавита оценка Синглтона слабее оценки Хэмминга.
6. Неравенство Синглтона Для любого кода : с расстоянием выполняется неравенство Синглтона (называемое также оценкой или границей Синглтона).
В самом деле, пусть имеется кодовых слов в. Выделим в этих словах первые 1 позиций. Для некоторой пары кодовых слов эти позиций совпадают по принципу Дирихле (число слов больше числа вариантов 1 ). Расстояние между такими словами не больше ( 1) = + 1, что и требовалось доказать.
Для кодов в двухбуквенном алфавите эта оценка уступает оценке Хэмминга. А именно, для кода с расстоянием она оценивает сверху коэффициент полезного действия (скорость) кода величиной 1 /, что соответствует прямой, соединяющей точки (0, 1) и (1, 0) (рис. 2). Видно, что эта прямая соединяет концы кривой Хэмминга и лежит выше неё.
Для большего размера алфавита это уже не так. Дело в том, что оценка Хэмминга не даёт ничего хорошего при. Рассмотрим, например, случай = 3 и шар радиуса /2 или чуть меньше. Сколько элементов в этом шаре? Позиций несовпадения примерно /2 среди ; вариантов выбора не более 2. После такого выбора останется выбрать в каждой позиции несовпадения один из двух несовпадающих символов, получится не более 2/2.
Таким образом, шар радиуса не более /2 содержит не более 2 = (2 2) элементов. А всего в пространстве 3 точек, поэтому оценка на число шаров будет всего лишь (3/2 2) и кривая Хэмминга не стремится к нулю при приближении к (в отличие от прямой Синглтона).
Кодируемое слово. 1 (где = F ) будем рассматривать как последовательность коэффициентов многочлена степени меньше. Ему соответствует кодовое слово, состоящее из значений многочлена в заранее выбранных точках поля F (естественно, что для этого надо, чтобы ). Из курса алгебры известно, что два различных многочлена степени меньше могут совпадать максимум в 1 точках. Поэтому для различных многочленов имеется как минимум +1 точек (среди выбранных нами ) несовпадения, то есть кодовое расстояние построенного кода Рида < Соломона не меньше +1. Тем самым для этих кодов неравенство Синглтона обращается в равенство.
Кодирование выполняется просто. Некоторая проблема тут с декодированием: как восстановить многочлен по таблице значений, где некоторые значения испорчены? Оказывается, что это можно сделать за полиномиальное время (чего с первого взгляда не скажешь).
Поскольку число ошибок не больше, существует (пока что неизвестный нам) многочлен () степени, который обращается в нуль в местах ошибок. (Достаточно перемножить одночлены ( ) для всех, где есть ошибки; если таких мест меньше, домножим результат ещё на что-нибудь, чтобы поднять степень до.) Тогда ()() равно ()() во всех точках, поскольку разница между () и () ()() имеет степень меньше +. Таким образом, верна Лемма 1.
меньше +, для которых ()() = () во всех точках.
Удобно договориться, что старший коэффициент многочлена (при ) равен единице, а остальные могут быть произвольными. (То, что страший коэффициент равен единице, автоматически означает, что многочлен () имеет степень ровно ). Тогда лемму 1 можно считать утверждением о разрешимости некоторой системы линейных уравнений. Неизвестными в ней являются остальные коэффициентов многочлена и + коэффициентов многочлена (всего + 2 штук), а уравнений в ней (что не меньше + 2, хотя нам это и не важно).
Тем самым некоторые многочлены, удовлетворяющие условиям леммы 1, можно найти, решив эту систему. Правда, пока мы не знаем, как они связаны с «настоящими» и. Об этом говорит Пусть () и () | произвольные многочлены, удовлеЛемма 2.
творяющие условиям леммы 1 (это значит, что они имеют нужные степени и равенство ()() = () выполняется во всех точках). Тогда (б) частное / равно исходному (и искомому) многочлену.
Они совпадают во всех тех точках, где =, а таких точек как минимум +, поэтому эти многочлены равны.
в том, что поле F | вещь абстрактная. Оно единственно с точностью до изоморфизма, но не имеет какого-то «канонического» представления. Можно доказать, что его элементы можно представить числами 0. 1 таким образом, что операции сложения, вычитания, умножения и деления выполняются за полиномиальное от log время. При использовании такого представления алгоритм декодирования и будет полиномиальным от и log.
Можно рассматривать также задачу о декодировании с Замечание 2.
ошибками и пропусками (или, как обычно говорят, «стираниями»). Под пропуском мы понимаем позицию, в которой буква неизвестна. (Это лучше, чем неверная буква, так как мы хотя бы знаем, в какой позиции проблема.) Видно, что для декодирования кода Рида < Соломона нужно, чтобы число пропусков плюс удвоенное число ошибок не превосходило (поскольку пропуск одной позиции даёт снова код Рида < Соломона с заменой на 1). Так что пропуск считается за пол-ошибки («два переезда | как один пожар»).
Всем хороши эти коды, но только они требуют достаточно большого алфавита (размер алфавита должен быть не меньше длины кодовых слов, да ещё быть степенью простого числа). Уменьшить алфавит можно, используя конструкцию каскадных кодов, описываемую в следующем разделе.
9. Каскадные коды Пусть имеется некоторый код с большм алфавитом. Можно ли его переделать в код с меньшим (скажем, двоичным) алфавитом? Например, пусть содержит 2 букв. Тогда можно записать каждую букву из с помощью блока из битов. При этом код превратится в код Кодовое расстояние при этом не уменьшится. В самом деле, если для исходного кода оно было, то теперь два кодовых слова отличаются по крайней мере в блоках, а отличие в блоке означает отличие хотя бы в одном бите этого блока.
Общая длина кодовых слов, однако, возрастёт (в раз), так что допустимый процент ошибок в кодовом слове уменьшится в раз.
2 Если | простое число, то это совсем просто (для деления надо использовать алгоритм Евклида). Если | степень простого числа (других полей не бывает), то есть = для простого и некоторого 1, то такое поле изоморфно фактор-кольцу F [ ] по идеалу, порождённому неприводимым над F многочленом степени, и сложность только в том, как найти такой неприводимый многочлен (умножать, делить и применять алгоритм Евклида для многочленов можно быстро). Алгоритмы поиска неприводимых многочленов | целая наука; оказывается, что это можно делать детерминированно за полиномиальное от и время, а вероятностно | за полиномиальное от log и (то есть от log ) время.
Более надёжный двоичный код получится, если кодировать буквы алфавита блоками не из битов, а из большего числа битов, причём использовать при этом какой-либо код, исправляющий ошибки.
В общем случае такая конструкция «каскадного кода», или «конкатенации» двух кодов, применима к кодам если | | = | |. Тогда каждую букву алфавита можно рассматривать как блок из символов алфавита и кодировать блоком из символов алфавита.
Формально, определим конкатенацию «внешнего» кода и «внутреннего» кода как код Чтобы найти значение на слове длины, составленном из букв алфавита, это слово надо разбить на блоков длины. Если эти блоки считать буквами алфавита, получится слово длины в алфавите.
Применив к нему код, получим слово из блоков длины. Остаётся закодировать каждый из этих блоков по отдельности кодом, получив блоков длины, или всего букв алфавита.
Кодовое расстояние конкатенации кодов не меньше произТеорема.
ведения их кодовых расстояний.
В самом деле, рассмотрим два различных кодовых слова в конкатенации. Каждое из них состоит из блоков длиной. Условие на код гарантирует, что имеется по крайней мере различных блоков. (Через, мы обозначаем кодовые расстояния кодов и.) Условие на код гарантирует, что в каждой паре различных блоков имеется (как минимум) отличающихся букв, всего получается различий.
Таким образом, каскадный код позволяет исправлять около / ошибок (половина кодового расстояния). Но как именно это сделать?
Чтобы этот алгоритм работал, в декодируемом слове должно быть не более блоков с более чем ошибками (где и | допустимые числа ошибок для кодов и ). Это заведомо будет так, если общее число ошибок (во всех блоках) не больше. Учитывая, что /2, мы видим, что такой алгоритм позволяет исправлять примерно / ошибок, что составляет четверть кодового расстояния и вдвое меньше максимально допустимого числа ошибок (которое примерно равно половине кодового расстояния).
Если общее число ошибочных позиций (среди поданных на вход описанного алгоритма) меньше, то описанный процесс позволит правильно декодировать исходное слово хотя бы при одном значении параметра.
Прежде чем доказывать лемму, заметим, что она не говорит, как найти хорошее значение параметра | но это и не нужно. Мы можем перепробовать все значения (их число заведомо не превосходит, поэтому этот перебор не повредит полиномиальности алгоритма) и затем проверить полученные результаты с помощью кодирования (правильный должен давать менее /2 отличий).
Осталось доказать лемму. Предположим, что некоторое выбрано.
Числа нам неизвестны, но мы знаем, что:
может быть сочтён неизвестным или быть принятым за другой блок).
Таким образом, для данного все индексы = 1, 2. делятся на три категории (задаваемые тремя указанными неравенствами на ).
Количество таких индексов обозначим через (), () и () соответственно. Нам достаточно доказать, что при некотором (из промежутка 0. ) выполняется неравенство ()+2(). (Реальная ситуация может быть даже немного лучше, если блок с большим числом ошибок не был принят за другой блок, а был сочтён неизвестным.) Чтобы доказать существование такого значения, достаточно установить, что среднее значение величины () + 2() меньше. При усреднении мы считаем все значения от 0 до равновероятными, то есть речь идёт просто о среднем арифметическом. А кодируемое слово, его код и внесённые в него ошибки (и, тем самым, чсла ) мы считаем фиксированными.
В силу аддитивности математического ожидания (линейности среднего арифметического) можно вычислить средний вклад каждого отдельного, а потом сложить их по всем. Итак, пусть фиксировано некоторое (и, тем самым, значение ).
вторую попадём, когда. Вероятность этого события (она же | вклад в интересующее нас среднее) есть /( + 1).
Если, то мы попадём либо во вторую категорию, либо в третью | последнее случится, если. Вероятность последнего события равна поэтому математическое ожидание вклада позиции в + 2 не превосходит (мы использовали при оценке, что 2 +1 : таково соотношение между числом исправляемых ошибок и кодовым расстоянием для внутреннего кода).
Заметим, что полученная только что оценка верна (хотя и тривиальна) Таким образом, среднее в обоих случаях не превосходит / для данного и / в сумме, что по предположению леммы меньше (ведь есть общее число ошибок в кодовом слове каскадного кода).
11. Теорема Форни Будем рассматривать двоичные коды с возрастающей длиной кодового слова и требовать, чтобы доля исправляемых ошибок (/ в наших обозначениях) и коэффициент полезного действия кода (/ в наших обозначениях) были отделены от нуля.
Существование таких кодов очевидно следует из оценки Варшамова < Гилберта.
Но если мы хотим, чтобы алгоритмы кодирования и декодирования были бы достаточно эффективны (скажем, полиномиальны по, длине кодового слова), требуется более сложная конструкция.
Объясним это более подробно. При построении каскадного кода коэффициенты полезного действия перемножаются, как и доли исправляемых ошибок (даже если не использовать улучшенный алгоритм декодирования из предыдущего раздела). Поэтому нам нужно всего лишь, чтобы для каждого из двух кодов коэффициент полезного действия и доля исправляемых ошибок были отделены от нуля.
Для наглядности возьмём какой-нибудь пример с конкретными значениями параметров. Фиксируем натуральное и рассмотрим поле F из 2 элементов. Кодируемое слово будет состоять из 21 блоков (число блоков | половина размера поля). Каждый блок содержит битов, то есть представляет собой элемент поля F. Мы считаем блоки коэффициентами многочлена степени меньше 21. Внешним кодом является код Рида < Соломона: от коэффициентов этого многочлена мы переходим к его значениям во всех 2 точках поля. При этом число блоков удваивается.
Далее мы кодируем по отдельности каждый блок с помощью внутреннего кода. Будем считать, что при кодировании блок удлиняется вдвое (из битов получается 2). Граница Варшамова < Гилберта (рис. 1 на с. 9) показывает, что при этом можно добиться кодового расстояния 10% (от длины кодового слова, в данном случае 2) и исправления 5% ошибок.
В итоге конкатенация кодов увеличивает число битов в 4 раза и имеет кодовое расстояние 5% (от длины слова). При этом тривиальный алгоритм декодирования позволяет исправлять 1,25% ошибок, а улучшенный | 2,5%.
Декодирование внутреннего кода при этом происходит с помощью перебора всех кодовых слов внутреннего кода (что допустимо, так как их не более 2 ).
Вместо использования поля из 2 элементов можно было Замечание.
бы (с чуть худшими параметрами) использовать поле вычетов по простому модулю между 2 и 2+1. Такое простое число существует («постулат Бертрана», он же теорема Чебышёва), и найти его можно перебором (полиномиальное от 2 число вариантов).
Не всегда код хорош. Например, при = 0 мы дописываем нули, что совсем бессмысленно; при = 1 мы дублируем каждый бит слова, что тоже ничего хорошего не даёт. Но оказывается, что при малых доля тех F, при которых кодовое расстояние кода больше, близка к единице. Это следует из такой леммы:
кодовое расстояние не более, не превосходит Поскольку (, ) 2, при малых / это отношение, примерно Доказательство расстояние для не больше. Поскольку код линеен, это значит, что найдётся такое ненулевое слово, при котором общее количество единиц в битовых строках и не больше. В частности, слова и находятся в шаре радиуса с центром в нуле. Тогда коэффициент представим в виде дроби, числитель и знаменатель которой лежат в указанном шаре, а таких дробей не больше, чем квадрат числа элементов шара, то есть (, ). А всего в поле F имеется 2 элементов, что и даёт указанную оценку.
Этот код имеет коэффициент полезного действия 25% (удлиняет слова в четыре раза). Кодовое расстояние этого кода (делённое на длину кодового слова, то есть в расчёте на один символ) отделено от нуля, как и в конструкции Форни.
Это можно доказать примерно так: при некотором 0 доля тех F, при которых кодовое расстояние кода (в расчёте на символ) меньше, не превосходит 1%. А один процент блоков внешнего кода не может сильно повлиять на его кодовое расстояние.
1. При этой конструкции построение кода и кодирование не требуют перебора. Однако декодирование внутреннего кода (в тех блоках, где оно удаётся) по-прежнему требует перебора всех возможных кодовых слов.
13. Оценка Плоткина Различие между границами Хэмминга и Гилберта особенно разительно в правой половине рис. 1: при /2 граница Хэмминга не запрещает существования кодов, а граница Гилберта не гарантирует их существования. Что же происходит на самом деле? (Речь идёт о двоичных кодах, когда = <0, 1>.) Максимальное расстояние между двумя элементами B равно. Точки, между которыми такое расстояние, отличаются во всех позициях, и потому ясно, что три точки с попарными расстояниями найти нельзя.
Более того, даже если ослабить требования и искать три точки с попарными расстояниями не меньше 0,99, это тоже не удастся: если и отличаются от в 99% мест, то совпадает с по крайней мере в 98% мест.
Аналогичное утверждение, хотя и не по столь очевидным причинам, справедливо для любой доли 1/2.
Пусть 1/2. Количество точек в B, попарные расстояния между которыми не меньше, не превосходит Здесь важно, что оценка на число точек не зависит от (хотя и зависит от : чем ближе к 1/2, тем слабее оценка).
Доказательство единиц рассматривать последовательности единиц и минус единиц, считая их векторами в R. Определим скалярное произведение в R, положив Разница с обычным скалярным произведением в R состоит лишь в дополнительном делении на. Это технически удобно, поскольку при этом евклидова длина любого слова (которое, напомним, мы считаем вектором из плюс-минус единиц) равна 1.
Если расстояние Хэмминга между двумя кодовыми словами не меньше, то их скалярное произведение отрицательно и не больше 1 2.
Теперь легко получить оценку на число векторов: если имеется единичных векторов. в евклидовом пространстве и при этом скалярное произведение любых двух из них не больше 1 2, то (имеется квадратов и ( 1) векторов), откуда что и требовалось в лемме.
Таком образом, если мы хотим, чтобы количество передаваемой информации росло с ростом, на исправление более чем 25% ошибок надеяться не приходится. В частности, в правой половине рис. 1 никаких интересных кодов нет, хотя оценка Хэмминга их и не запрещает.
Если требовать, чтобы кодовое расстояние было больше 50% (разрешая ему быть сколь угодно близким к 50%), то все углы между кодовыми словами будут тупыми и число точек не больше + 1, как показывает следующее простое утверждение:
Если несколько векторов евклидова пространства образуют попарно тупые углы, то после удаления любого из векторов получается линейно независимая система.
В самом деле, предположим, что векторы. образуют попарно тупые углы. Покажем, что. линейно независимы. Пусть это не так и Вычеркнем все нулевые коэффициенты. Если оставшиеся коэффициенты имеют один знак, то умножим скалярно на и получим противоречие:
сумма нескольких отрицательных скалярных произведений с коэффициентами одного знака равна нулю.
Если оставшиеся коэффициенты имеют разные знаки, то разнесём их в разные части и получим равенство где все коэффициенты положительны. Если обе части равны нулю, то смотри выше. Если же нет, то скалярное произведение левой части на правую одновременно положительно (как скалярный квадрат вектора) и отрицательно (как сумма отрицательных скалярных произведений с положительными коэффициентами). Линейная независимость доказана.
В самом деле, можно взять плюс-минус векторы базиса, их как раз 2.
Больше векторов взять не удастся:
-мерном евклидовом пространстве образуют поЕсли векторы в парно прямые или тупые углы, то их число не превосходит В самом деле, можно считать, что линейная оболочка векторов совпадает со всем пространством (иначе можно свести дело к меньшей размерности, рассуждая по индукции) и векторы. образуют базис.
Выразим остальные (при ) через.
Заметим, что в таких выражениях все ненулевые коэффициенШаг 1.
ты (а в каждом из выражений они есть, поскольку = 0) отрицательны.
В самом деле, предположим, что это не так и в каком-то из выражений есть положительные. Перенесём все отрицательные коэффициенты в левую часть и получим равенство где все коэффициенты при положительны и в правой части что-то осталось (ведь были положительные коэффициенты). Тогда правая часть этого равенства (а значит, и левая) отлична от нуля в силу линейной независимости векторов базиса. Произведение левой части на правую должно быть одновременно положительно (как скалярный квадрат ненулевого вектора) и неположительно (поскольку после раскрытия скобок становится суммой неположительных скалярных произведений с положительными коэффициентами). Противоречие.
где все коэффициенты положительны. Обе части содержат хотя бы один ненулевой член и потому не равны нулю (как мы уже знаем про линейные комбинации с коэффициентами одного знака). Поэтому скалярное произведение левой части и правой одновременно положительно (как скалярный квадрат ненулевого вектора) и неположительно (как сумма неположительных скалярных произведений с положительными коэффициентами). Противоречие.
Таким образом, мы приходим к оценке (границе) Плоткина: число кодовых слов длины с попарными расстояниями не меньше /2 не превосходит 2.
14. Улучшение оценки Синглтона Имея оценку Плоткина, вернёмся к рассуждению, использованному для доказательства оценки Синглтона, и получим более сильную оценку.
Будем рассматривать случай кодов в двухбуквенном алфавите.
Доказывая оценку Синглтона, мы брали = 1 и замечали, что для полученного кода (с двумя кодовыми словами) расстояние не больше длины кодового слова:
Теперь мы можем взять меньшее, при котором у полученного кода длина кодового слова будет равна удвоенному расстоянию:
Согласно оценке Плоткина, число кодовых слов не превосходит удвоенной длины:
Замечая, что и деля на, получаем оценку При большх последним слагаемым можно пренебречь и на рис. появляется новая граница (пунктир на рис. 3).
Видно, что она кое-где сильнее, а кое-где слабее границы Хэмминга.
15. Код Адамара Оказывается, что оценка Плоткина является точной, если есть степень двойки. Соответствующий пример доставляют коды Адамара.
Такая функция задаётся своими значениями в 2 = вершинах, и эти значения образуют слово длины, надо только фиксировать какой-либо порядок на вершинах куба.
В качестве кодовых слов возьмём аффинные функции, то есть функции вида при. B (умножение и сложение | как в поле из двух элементов). Такая функция задаётся набором своих коэффициентов, и потому имеется 2+1 = 2 аффинных функций.
Две такие функции либо различаются во всех точках (если отличаются лишь коэффициентом ), либо ровно в половине точек (образующих аффинное подпространство коразмерности 1 над полем B). Код Адамара построен.
С точки зрения структуры евклидова пространства R, о котором мы говорили в разделе 13, кодовые слова кода Адамара являются плюс-минус базисными векторами ортонормированного базиса (замена знака соответствует добавлению единицы к аффинной функции, то есть изменению Итак, к настоящему времени у нас есть три явные конструкции кодов для двухбуквенного алфавита: код Хэмминга, код Форни < Юстесена < Возенкрафта и код Адамара. Код Хэмминга имеет коэффициент полезного действия, близкий к 100%, но исправляет только одну ошибку. Напротив, код Адамара исправляет почти что максимально возможное число ошибок (до 25%), но зато имеет очень малый коэффициент полезного действия. Код Форни занимает промежуточное положение: у него и доля исправляемых ошибок, и коэффициент полезного действия отделены от нуля, хотя и невелики.
Мы знаем, что в коде Адамара кодовое расстояние равЗамечание.
но 50%. Однако у кода Адамара длина кодового слова экспоненциально больше длины исходного сообщения ( = 2 ). Если мы хотим явно указать код, у которого кодовое расстояние приближается к 50% (и границе Плоткина), а длина кодовых слов полиномиальна (от длины кодируемого сообщения), то можно использовать каскадный код, в котором внутренним кодом является код Адамара, а внешним | код Рида < Соломона.
В самом деле, рассмотрим код Адамара с 2+1 кодовыми словами размера 2. Используя его как внутренний код, мы получаем для внешнего кода алфавит из 2+1 символов. Для простоты записи формул пожертвуем половиной и будем использовать лишь 2 из них. Зафиксируем некоторое 0. Внешний код Рида < Соломона будет кодировать 2 таких символов (блоков из битов) с помощью 2 символов (блоков), каждый из которых при внутреннем кодировании изображается 2 битами.
Таким образом, мы можем достичь кодового расстояния, сколь угодно близкого к 50% (при малом фиксированном ). При этом длина кодового слова ограничивается примерно квадратом длины кодируемого слова.
Можно ли это делать за полиномиальное время? Постановка этого вопроса требует уточнения: полиномиальное время от чего? От длины кодируемого слова или длины кодового слова? Поскольку мы кодируем + 1 битов с помощью 2 битов, разница весьма существенна.
Тривиальный ответ таков: за полиномиальное от 2 время мы можем перебрать все 2+1 возможных кодируемых слов и найти нужное, а за полиномиальное от время мы сможем прочесть лишь пренебрежимо малую часть кодового слова, и вся эта часть может попасть в зону ошибок, так что декодирование невозможно.
(Более аккуратное рассуждение: проведём декодирование для какогото одного случая, скажем, нулевого слова, потом посмотрим, какие позиции в кодовом слове мы прочли, и во всех кодовых словах эти позиции сделаем нулевыми; доля ошибок будет невелика, а декодирование разрушено.) Другое возможное уточнение: говоря о декодировании слова длины 2 за полиномиальное от время, будем предполагаеть, что это слово задано нам как «оракул»: по номеру бита (этот номер имеет длину ) нам сообщают значение соответствующего бита. (Это уточнение необходимо, поскольку, скажем, давать на вход слово длины 2 на ленте бессмысленно | в этом случае реально будет доступно лишь его начало полиномиальной длины.) Оказывается, что в данной постановке задачи декодирование за полиномиальное время может быть выполнено вероятностным алгоритмом со сколь угодно малой вероятностью ошибки. Точная формулировка:
роятностный алгоритм, который, получив число и (в виде оракула) кодовое слово длины 2 с не более чем 2 ошибок, работает полиномиальное от время и правильно декодирует слово с вероятностью не менее 1.
(Заметим, что полином, ограничивающий время работы, зависит от и от : чем ближе к 1/4 и чем меньше, тем дольше работает алгоритм.) Доказательство.
аффинной функции : B B, имеющей вид в случайной точке с вероятностью ошибки не больше. Коэффициент можно записать как разность значений в двух точках, отличающихся по первой координате:
Если в качестве (. ) взять случайную равномерно распределённую точку, то сдвинутая точка ( + 1. ) также будет равномерно распределена (хотя, конечно, эти две точки не будут независимы). Каждое из двух значений нам известно с вероятностью ошибки не больше 2, поэтому правильное значение для будет получено с вероятностью не меньше 1 2 50%.
Повторяя это несколько раз (для независимых точек) и затем определяя ответ большинством, можно (как известно из теории вероятностей) быстро уменьшать вероятность ошибки и тем самым найти коэффициент со сколь угодно малой вероятностью ошибки. Аналогично найдём и все остальные, после чего уже можно находить (тоже голосованием по нескольким точкам).
Как известно из теории вероятностей, при таком повтореЗамечание.
В общем случае мы рассматриваем многочлены от переменных степени не выше над полем F. При этом степень понимается как суммарная степень по всем переменным. (При = 1 получаются коды Рида < Соломона, при = 1 | коды Адамара.) Алфавит состоит из символов (элементов поля); коэффициенты многочлена степени не выше образуют кодируемое слово, а значения этого многочлена во всех точках F | кодовое слово.
Длина кодового слова равна, а длина кодируемого слова равна числу решений неравенства в неотрицательных целых числах, то есть (решение такого неравенства задаётся разбиением ряда из объектов на + 1 групп с помощью перегородок; числа. | числа объектов между перегородками; объекты справа от последней перегородки не входят ни в одно и составляют разницу между частями неравенства).
Оценка кодового расстояния основана на следующем простом алгебраическом утверждении:
член от переменных над этим полем, причём его степень (суммарная по всем переменным) равна. Тогда доля точек (. ) F, для которых не превосходит /.
Лемма очевидна, если многочлен содержит член стеДоказательство.
пени, в который входит только одна переменная. Тогда при любых значениях остальных переменных получается ненулевой многочлен степени, имеющий не более корней, так что на каждой прямой (когда все остальные переменные фиксированы) доля нулей не больше /, и остаётся их усреднить.
К этому случаю можно пытаться сводить произвольный многочлен линейной невырожденной заменой переменных (которая не меняет суммарную степень); проще, однако, доказать утверждение леммы индукцией по числу переменных. Для = 1 утверждение леммы очевидно (число корней многочлена от одной переменной не превосходит его степени).
Для произвольного рассуждаем так. Выделим какую-нибудь переменную, например,, и рассмотрим моном с максимальной степенью по. Пусть эта степень равна ; очевидно,. Запишем как многочлен по, коэффициенты которого суть многочлены от. Коэффициент при представляет собой некоторый многочлен (. ) степени не больше. Случай = 0 мы уже обсуждали. В общем случае для равномерно распределённых случайных. вероятность события по предположению индукции не превосходит ( )/, а вероятность события не превосходит /, поскольку для каждого набора значений. при которых (. ) = 0, существует не более значений, при которых (. ) = 0. (Так что даже и условная вероятность не превосходит /.) Складывая вероятности, получаем искомую оценку /. Лемма доказана.
Таким образом, кодовое расстояние не меньше (1 /), то есть (1 /) в расчёте на один символ. Например, при = 1 и = получается расстояние 50%, как мы уже видели для кодов Адамара.
Ещё один пример: пусть = 2. Кодовое слово состоит из символов, а кодируемое слово из = ( + 1)( + 2)/2 /2 символов.
Эти коды названы БЧХ (в английском варианте | BCH) по именам своих изобретателей: Боуза (Bose), Чоудхури (Ray-Chaudhuri) и Хоквингема (Hocquenghem). Они позволяют исправлять любое фиксированное число ошибок над двухбуквенным алфавитом и примыкают к коду Хэмминга (который является их частным случаем).
Все такие таблицы и являются кодовыми словами кода БЧХ.
Переформулировка: слово из нулей и единиц является кодовым словом кода БЧХ, если соответствующий ему многочлен (принимающий указанные значения в точках поля F) имеет степень меньше.
Для этого нам понадобятся некоторые сведения из алгебры. В поле F выделим подполе F F, состоящее из нуля и единицы. [Чтобы убедиться, что это действительно подполе, достаточно проверить, что 1 + 1 = в F, то есть что характеристика поля F равна 2. Это доказывается так:
Однако на самом деле ситуация оказывается ещё немного лучше:
условий, соответствующих обращению в нуль старших коэффициентов многочлена, линейно зависимы над полем F. Чтобы понять это, нам понадобится вспомнить ещё кое-что из алгебры.
Для начала заметим, что условие «все значения многочлена | нули или единицы» можно переформулировать так: () = () для всех F. Другими словами, многочлен должен обращаться в нуль во всех точках поля F. Это не значит, что все его коэффициенты нулевые (ведь степень многочлена может быть почти в два раза больше числа элементов в поле), а означает лишь, что делится на многочлен Последний многочлен равен. Действительно, по теореме Лагранжа порядок каждого элемента в мультипликативной группе поля делит порядок группы, равный 1 (на самом деле верно более сильное свойство: мультипликативная группа поля обязана быть циклической; но это сейчас нам не важно). Поэтому 1 = 1 для любого ненулевого элемента поля, и = для любого элемента поля. Значит, многочлен обращается в нуль во всех точках поля, поэтому он делится на ; остаётся заметить, что у этих двух многочленов совпадают степени и старшие коэффициенты.
Итак, условие «все значения | нули или единицы» можно переформулировать так: делится на многочлен без остатка.
Дальнейшие уравнения системы выражают 3, 5. через с бльшими индексами. Поэтому условия обращения в нуль достаточно записывать лишь для 2, 4. вплоть до (для чётного ) и +1 (для нечётного ).
Интересно сравнить параметры БЧХ-кодов с границей Хэмминга. Шар радиуса = /2 содержит примерно /! элементов (мы считаем, что и потому заменяем ( 1). ( + 1) на ). Граница Хэмминга говорит, что логарифм числа кодовых слов не превосходит примерно первые два слагаемых как раз соответствуют БЧХ-кодам, так что разница лишь на log(!).
19. БЧХ и Хэмминг Покажем, что код Хэмминга может быть получен как частный случай кода БЧХ.
Пусть, например, = 3, = 8 и мы рассматриваем поле F. Многочлен однозначно определяется своими значениями в 8 точках этого поля (и, с другой стороны, однозначно определяется 8 коэффициентами. ). Условие « принимает лишь значения 0 и 1» запишется как система уравнений Наложив ограничение = 0, мы получим код размерности 7 (одно уравнение на 8 переменных) с расстоянием 2. Легко понять, что это за код:
поскольку расстояние равно 2, то в уравнение обязаны входить все переменные, и это уравнение есть проверка на чётность (сумма по модулю равна нулю).
Следующее ограничение = 0. Оно соответствует трём уравнениям и уменьшает размерность кода до 4 (или больше, если уравнения были бы зависимыми | как мы увидим, это не так). Из уравнения = видно, что в этом случае и = 0, так что кодовое расстояние будет не меньше 4. Выбросив любой бит, мы не изменим размерность кода (поскольку по условию чётности он определялся остальными) и уменьшим расстояние не более чем на 1. Получится код длины 7 и размерности 4 с кодовым расстоянием не меньше 3 | всё как у кода Хэмминга. (Отсюда следует, что уравнения были независимыми, поскольку код Хэмминга и так заполняет всё пространство и больше кодовых слов просто не поместится.) Чтобы убедиться, что это и есть код Хэмминга, надо выяснить, как от значений многочлена в точках поля перейти к его коэффициентам.
Это делается по интерполяционной формуле Лагранжа:
где | многочлен (степени меньше ), равный 1 в точке и 0 в остальных точках поля. В данном случае в качестве такого многочлена можно взять В самом деле, при = первое слагаемое равно 1 (порядок мультипликативной группы поля, равный 1, делится на порядок любого её элемента), и многочлен обращается в нуль (наше поле характеристики 2).
Разложение ( )1 по биному Ньютона даёт (в поле характеристики 2) многочлен В этом можно убедиться, вспомнив, что в строке треугольника Паскаля, номер которой на единицу меньше степени двойки, все члены нечётные.
А можно домножить записанную сумму на ( ), получится, что равно ( ) (поскольку возведение в квадрат, а также в любую степень двойки, перестановочно со сложением).
Так или иначе, мы можем теперь записать более конкретно условия обращения в нуль коэффициентов и в терминах значений многочлена. Как видно из формулы Лагранжа и формулы для, Поэтому условие на представляет собой проверку на чётность (это мы и так знаем из общих соображений). Условие на представляет собой равенство в поле F, которое можно рассматривать как векторное пространство размерности 3 над F. При этом семь ненулевых элементов превращаются в семь ненулевых векторов из F, то есть в векторы (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1), и условия на коэффициенты () при = 0 будут те самые, что были в коде Хэмминга. Поэтому из кода БЧХ получается код Хэмминга, если отбросить (0), как мы и говорили.
В этом примере мы считали, что = 3 ( = 8), но всё сказанное очевидно переносится и на случай произвольного.
20. Декодирование списком До сих пор мы требовали, чтобы исправление ошибок происходило однозначно. Посмотрим, что будет, если ослабить это требование и разрешить до вариантов декодирования (при некотором ). Более формально, множество кодовых слов должно быть таким, чтобы любой шар радиуса содержал не более кодовых слов. В этом случае мы говорим, что код допускает декодирование списком длины (с исправлением ошибок).
Как и раньше, нас интересует возможность построения такого множества при заданных параметрах (размер алфавита), (длина кодируемого слова), (длина кодовых слов), (число возможных ошибок) и, наконец,. (Случай = 1 соответствует прежней постановке задачи.) Аналог границы Хэмминга теперь выглядит так:
В самом деле, шары радиуса в количестве штук содержат по (, ) элементов каждый и покрывают множество из элементов не более чем в слоёв.
В логарифмической шкале:
Таким образом, если рассматривать не слишком большие (скажем, полиномиальные от ), то граница почти не сдвигается.
Зато сдвигается другая граница: указанное только что необходимое условие существование кода оказывается почти что достаточным. А именно, верно такое утверждение (теорема Элайеса):
Пусть выполнено неравенство Хэмминга (в прежней форме, Теорема.
Тогда существует код, допускающий декодирование списком длины, где = ( log ).
декодирование списком длины с положительной вероятностью (или, другими словами, что число кодов, не допускающих такого декодирования, меньше общего числа кодов).
считаем число плохих | тех, где некоторое слово покрывается (или более) шарами. Плохое отображение можно задать, указав плохое слово (покрытое или более шарами) [ вариантов];
индексы покрывающих шаров [подмножество размера в множестве, всего вариантов];
центры покрывающих шаров (= кодовые слова, попадающие в шар радиуса с центром в точке, выбранной на первом шаге) [ точек в шаре, всего (, ) вариантов];
остальные кодовые слова [ точек, всего ( ) вариантов].
Если немного уменьшить пропускную способность конЗамечание.
струируемого кода, предположив, что (для маленькой константы 0), то в левой части оценок добавится множитель (( ) ), меньший единицы, поскольку тогда и останется неравенство которое выполняется при = (1) (величина зависит от выбора и, но не растёт с ростом ). В самом деле, достаточно взять, при котором Мы доказали существование кодов, декодируемых списком, вблизи границы Хэмминга, но не указали явно этих кодов. Сложность описания построенных кодов экспоненциальна, не говоря уже о времени кодирования и декодирования.
21. Кодовое расстояние и декодирование Пусть имеется код : с минимальным расстоянием между кодовыми словами. Мы уже знаем, что он позволяет декодировать ошибок при /2. Переходя от различающихся позиций к совпадающим, можно переформулировать это так. Пусть известно, что любые два кодовых слова совпадают максимум в (= ) позициях. Тогда для любого слова не более одного кодового слова может совпасть с более чем в ( + )/2 (= /2) позициях.
В этих же обозначениях удобно формулировать утверждение о декодировании списком, заменив среднее арифметическое на среднее геометрическое:
Пусть любые два кодовых слова (из ) совпадают максиТеорема.
мум в позициях. Тогда для любого слова не более чем + слов могут совпадать с ним более чем в позициях.
(Заметим, что среднее геометрическое меньше среднего арифметического, так что всё согласовано.) лее чем в позициях (каждое в своих). Пусть <1, 2. >| номера позиций, где совпадает с. Тогда каждое из множеств содержит более элементов, а пересечение при = содержит не более элементов.
Рассмотрим характеристические функции множеств как случайные величины на вероятностном пространстве <1. >(с равномерным распределением). Напомним, что корреляция двух случайных величин и определяется как где E | математическое ожидание (в данном случае | среднее арифметическое чисел). Другими словами, корреляция и есть скалярное произведение E и E.
Раскрывая скобки и пользуясь линейностью математического ожидания, получаем, что Для случая, когда случайные величины | индикаторы событий (равны единице, если событие произошло, и нулю, если не произошло), получаем формулу корреляция равна нулю, когда события независимы. В данном случае вероятность каждого события больше / = /, а вероятность пересечения любых двух не больше /, так что корреляции отрицательны.
Заметим, что если разрешить каждому содержать ровно элементов, то углы из тупых станут неострыми, и вместо + 1 получится 2 векторов.
Возвращаясь к исходным параметрам: если минимальное расстояние кода : равно, то код допускает декодирование ( +1)-списком с исправлением менее чем ( ) ошибок.
Доказанную теорему можно прочесть и так: при ( ) в шаре радиуса может содержаться не более чем +1 элементов с попарными расстояниями или более. (Имеется в виду расстояние Хэмминга Для кода с кодовым расстоянием 50% (в частности, для кода Адамара) эта теорема устанавливает возможность декодирования списком при доле ошибок 1 1/2 29%, что лишь немного больше границы в 25% для однозначного декодирования. Однако (в отличие от случая однозначного декодирования) даваемая этой теоремой оценка отнюдь не является точной. Например, для кодов Адамара возможно декодирование списком при любой фиксированной доле ошибок, меньшей 1/2. (Более точную оценку Джонсона мы приведём дальше.) 22. Декодирование списком кодов Адамара Пусть 0 | произвольное положительное число.
Число кодовых слов кода Адамара, которые отличаются от Теорема.
данного слова не более чем в (1)-доле позиций, не превосходит 1/.
плюс-минус базисными векторами ортонормированного базиса в евклидовом пространстве, если рассматривать кодовые слова как последовательности единиц и минус единиц и определять скалярное произведение по формуле (при этом есть степень двойки, но сейчас это не важно). Пусть | произвольное слово (рассматриваемое как последовательность единиц и минус единиц). Если слово отличается от него не более чем в (1 ) позициях, то Теперь надо в качестве взять все базисные векторы (с плюсом и минусом) и оценить, для скольких из них такое возможно. Из пары векторов и лишь один может удовлетворять этому неравенству; заменяя знаки у базисных векторов, можно считать, что это вектор с плюсом.
По теореме Пифагора (которую в данном случае называют равенством Парсеваля) квадрат гипотенузы, равен сумме квадратов сторон,, взятой по всем базисным векторам. В нашем случае, = 1, поэтому количество, при которых,, не превосходит 1/, что и требовалось доказать.
23. Оценка Джонсона Похожее утверждение можно доказать для любых кодов (над двухбуквенным алфавитом) с расстоянием около 50%. Вот точная формулировРазложение по этому базису соответствует преобразованию Фурье на группе B = (Z/2Z) ; элементы базиса соответствуют характерам этой группы.
Пусть код состоит из двоичных слов длины на расстоТеорема.
янии не меньше (1 ) для некоторого 0. Тогда он допускает декодирование списком при доле ошибок (1 ) и размере списка 2.
Мы сформулировали это утверждение в терминах кодов, но по существу речь идёт о точках в шаре: теорема утверждает, что в B шар радиуса (1 ) может содержать не более 2 точек с попарными расстояниями не меньше (1 ).
Как и в доказательстве оценки Плоткина, будем расДоказательство.
сматривать последовательности единиц и минус единиц, являющиеся векторами единичной длины в евклидовом пространстве R.
Пусть шар с центром имеет радиус (1 ) (в метрике Хэмминга) и содержит точки. причём расстояние (Хэмминга) между и не меньше (1 ) при любых =. В терминах скалярного произведения это означает, что Другими словами, угол между и острый и не слишком близок к прямому, в то время как угол между и достаточно близок к прямому или даже тупой.
Мы хотим доказать, что 2. Это было бы так, если бы углы между и были тупыми или прямыми (см. доказательство оценки Плоткина). Чтобы свести дело к этому случаю, вычтем немного из каждого. Для этого найдём, при котором Видно, что всё подобрано так, что годится =. Оценка Джонсона доказана.
Теперь мы возьмём шары большего радиуса, чем /2. Про них уже нельзя утверждать, что пересечений нет. Однако | при подходящем радиусе | оценка Джонсона позволяет утверждать, что любая точка покрыта небольшим числом шаров (поскольку шар с центром содержит небольшое число кодовых слов). Поэтому суммарный объём шаров превосходит объём всего пространства в небольшое число раз.
Конкретно: пусть код со словами длины в двухбуквенном алфавите имеет расстояние = (1 ). Шары радиуса (1 ) могут пересекаться, но кратность пересечений не превосходит 2. Получаем для кодов с расстоянием Переходя к логарифмам, используя приближённую формулу для (с шенноновской энтропией), деля на и пренебрегая множителем 2 (малым по сравнению с 2 при большх ), получаем асимптотическую граи ницу, показанную на рис. 4 пунктирной линией. Эта граница называется границей Элайеса < Бассалыго.
Как мы видели, для декодирования списком (полиномиального размера) достаточно иметь примерно правильных значений. Сейчас мы дадим новое доказательство этого факта, из которого можно извлечь алгоритм декодирования.
Сейчас мы будем делать то же самое, но с двумя отличиями:
многочлен уже не обязательно первой степени по ;
требуется не просто обращение в нуль выражения (, ), а обращение в нуль с некоторой кратностью.
Говорят, что многочлен (, ) обращается в нуль в точке (, ) с кратностью, если ( +, + ) как многочлен от и не имеет членов степени меньше. Кратность 1 означает просто (, ) = 0, кратность 2 означает, что и производные по и равны нулю, кратность 3 | обращение в нуль вместе со вторыми производными, и так далее.
Заметим, что обращение в нуль в данной точке есть линейное условие на коэффициенты многочлена ; обращение в нуль с кратностью представляет собой набор из 1 + 2 +. + = ( + 1)/2 условий. Тем самым мы можем подобрать искомый многочлен методом неопределённых коэффициентов, если только этих коэффициентов больше, чем условий во всех точках. Если при этом степень многочлена будет не слишком велика, то его обращение в нуль на многих точках кривой = () (где | исходный многочлен) гарантирует, что он обращается в нуль на всей этой кривой.
ную степень степень многочлена | наибольшая из степеней мономов. (Переменная считается имеющей вес, поскольку мы собираемся на её место подставлять многочлен степени.) Следующие леммы носят чисто алгебраический характер.
-взвешенную степень меньше, равна числу решений неравенства в целых числаx, 0. А это число не меньше площади треугольника, ограниченного прямыми +, 0, 0, которая равна /2 (половина произведения катетов и /). В самом деле, если нарисовать этот треугольник на клетчатой бумаге и взять любую точку (, ) внутри него (не на границе), то эта точка попадает в клетку с левым нижним углом (, ). Координаты этого левого нижнего угла целые и удовлетворяют неравенству, поэтому число целых решений неравенства не меньше площади треугольника (ведь он покрыт клетками).
ля F (все они различны, хотя одна из двух координат у некоторых пар может совпадать). Пусть. | произвольные натуральные числа.
(Пока всё как в лемме 1.) Пусть, наконец, многочлен () имеет степень не больше и (сумма весов точек (, ), через которые проходит его график, не меньше ). Тогда (, ()) является нулевым многочленом (равен нулю в кольце многочленов от одной переменной).
одной переменной ) имеет степень меньше. Если (, ) является корнем (, ) кратности, а ( ) =, то многочлен () имеет корень кратности. Поэтому у многочлена число корней с учётом кратности не меньше, а степень меньше. Следовательно, = 0, что и утверждает лемма.
от одной переменной, причём (, ()) = 0. Тогда (, ) делится на многочлен () в кольце многочленов от двух переменных.
(Равенство (, ()) = 0 понимается как равенство в кольце многочленов, то есть как равенство нулю всех коэффициентов; это, вообще говоря, более сильное утверждение, чем равенство во всех точках, если элементов в основном поле мало.) енты которого являются многочленами от, и разделим его уголком на (). Поскольку старший коэффициент делителя равен единице, при этом не появится никаких дробей, частное будет многочленом от и, а остаток | многочленом от (поскольку делитель имеет степень 1 по, остаток имеет степень 0 по ). Таким образом, Подставив теперь () вместо, получим, что () | нулевой многочлен, что и требовалось доказать.






. ДoI!!;7. от г. Екатеринбург о внесенииизменений в лесохозяйственный регламент Ивдельского лесничества, утвержденный приказом Министерства природных ресурсов Свердловской области от 31.12.2008.м 1747 В соответствии с подпунктом 1 пункта 1 статьи 83, пунктом 2 статьи 87 Лесного кодекса Российской Федерации, пунктом 9 приказа Федерального агентства лесного хозяйства Российской Федерации от. »










Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.