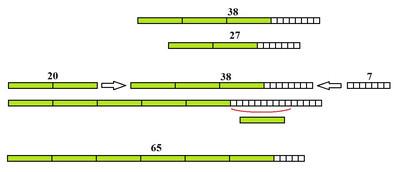
16 слив разложили на столе так как показано на рисунке ответ
ОЛИМПИАДА ПО МАТЕМАТИКЕ «ЮНЫЙ АРХИМЕД»4 КЛАСС
Ищем педагогов в команду «Инфоурок»
Задания школьного конкурса по математике «Юный Архимед»
ФИ ученика_____________________________ класс__________
1. ( 3 балла ) Прилетели галки, сели на палки. Если на каждой палке сядет по галке, то для
одной галки не хватит палки. Если же на каждой палке сядет по две галки, то одна из
палок будет без галок. Сколько было палок и сколько было галок? Обоснуйте ответ.
2. ( 4 балла ) Квадратный торт с четырьмя розочками надо разрезать
на 4 равных куска так, чтобы на каждом было по розочке. Нарисуйте,
3. ( 3 балла ) 16 слив разложили на столе так, как показано на рисунке.
Затем 6 слив съели, при этом в каждом горизонтальном и в каждом
вертикальном ряду осталось четное количество слив.
Нарисуйте, как лежат оставшиеся сливы.
составить квадрат. Нарисуйте.
6. ( 5 баллов ) На острове Буяне четыре королевства, причем каждое граничит с тремя
остальными. Нарисуйте карту острова так, как вы ее себе представляете.
Для того, чтобы покрасить кубик, изображенный на левом рисунке (Рисунок 14), понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображенную на правом рисунке?
8. ( 8 баллов ) Двое по очереди ломают плитку шоколада 7 × 8. За один ход разрешается
сделать прямолинейный разлом любого из кусков по углублению. Проигрывает тот, кто не
может сделать ход. Кто выиграет и каким образом? Обоснуйте ответ.
1. Ответ: галок – 4, палок – 3.
Количество галок на 1 больше, чем количество палок. При этом, количество галок
четно и половина этого количества на единицу меньше, чем количество палок.
Следовательно, галок – 4, палок – 3.
Можно рассуждать иначе. Если добавить одну палку, то галок и палок станет
поровну. Тогда, если на каждую палку сядет по две галки, то две палки будут лишними, а
две – занятыми. Следовательно, изначально галок – четыре, а палок – три.
Полное решение – 3 балла ; верный ответ без обоснований – 1 балл .
3. Ответ: Любой верный способ решения – 5 баллов .
4. Ответ: Любой верный пример – 4 балла ; вместо квадрата составлен прямоугольник –
5. Ответ: например, рисунок 5.
Нарисован любой из вариантов верного ответа – 3 балла
7.Ответ: Площадь поверхности первой фигуры равна 9*6=54, правой – 9+9+9+5+5+5+12=54. Так как площади равны, то краски понадобится столько же, т.е. 9 кг.
8. Ответ: выиграет первый.
Максимальное количество кусков, на которые можно разделить данную плитку
шоколада, – 56. Это осуществляется за 55 разломов. Следовательно, независимо от того,
как будет разламываться шоколадка, последний разлом сделает первый игрок.
Полное решение – 8 баллов ; ответ без всяких обоснований – 0 баллов .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО
Курс повышения квалификации
Скоростное чтение
Номер материала: ДБ-1046297
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Рособрнадзор открыл горячую линию по вопросам контрольных в школах
Время чтения: 1 минута
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
В Минобрнауки разрешили вузам продолжить удаленную работу после 7 ноября
Время чтения: 1 минута
Школьники Свердловской области с 8 ноября перейдут на дистанционку
Время чтения: 0 минут
Вузам Москвы и Подмосковья рекомендовали с 8 ноября ввести смешанный формат обучения
Время чтения: 1 минута
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
16 слив разложили на столе так как показано на рисунке ответ
1. Положите 3 спички на стол так, чтобы их головки не касались поверхности стола и друг друга.
а) уберите 2 спички так, чтобы образовалось 2 неравных квадрата;
б) переложите 3 спички так, чтобы образовалось 3 равных квадрата;
в) переложите 4 спички так, чтобы образовалось 10 квадратов.
а) уберите 4 спички так, чтобы образовалось 5 равных квадратов;
б) уберите 6 спичек так, чтобы образовалось 5 равных квадратов;
в) переложите 12 спичек так, чтобы образовалось 2 равных квадрата;
г) уберите 8 спичек так, чтобы образовалось 4 равных квадрата;
д) уберите 8 спичек так, чтобы образовалось 3 квадрата;
е) уберите 8 спичек так, чтобы образовалось 2 квадрата.
Дополнительные задачи 1
8. Из спичек составлено неверное равенство (см. рисунок).Переставьте одну спичку так, чтобы равенство стало верным.
Дополнительные задачи 2
11. Расположите 6 спичкек так, чтобы получилось 4 треугольника.
Олимпиада по математике школьный этап 2021 ВОШ задания и ответы для 4-11 класса
ПОДЕЛИТЬСЯ
Задания и ответы школьного этапа 2021 олимпиады по математике для 4-11 класса всероссийской олимпиады школьников 2021-2022 учебного года, официальная дата проведения олимпиады в Омске: 06.10.2021 (6 октября 2021 года)
Задания и ответы для 4 класса: скачать
Задания и ответы для 5 класса: скачать
Задания и ответы для 6 класса: скачать
Задания и ответы для 7 класса: скачать
Задания и ответы для 8 класса: скачать
Задания и ответы для 9 класса: скачать
Задания и ответы для 10 класса: скачать
Задания и ответы для 11 класса: скачать
Интересные задания и ответы олимпиады:
1)Ваня представил число 100 в виде суммы 14 слагаемых, имеющих одинаковую сумму цифр: 100=20+20+20+20+2+2+2+2+2+2+2+2+2+2 (сумма цифр числа 20 равна 2+0=2). Вася смог представить число 100 в виде суммы 11 слагаемых, имеющих одинаковую сумму цифр. Как он это сделал? Достаточно привести один пример такого представления.
Ответ: 100=50+5+5+5+5+5+5+5+5+5+5.
2)Вера, накопив 200 рублей, хотела купить пенал, но этих денег ей не хватило. Через несколько дней пенал уценили, и он стал стоить в два раза меньше. Теперь Вера смогла его купить и даже получила сдачу 15 рублей. Сколько стоил пенал первоначально? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 370 р.
3)Фермер огородил снаружи участок земли и разделил его на квадратики со стороной 3 м. В пяти квадратиках он разместил гусятники (обозначены «Г»), а в других пяти – будки со сторожевыми собаками (обозначены «С»). Но гуси нападают на собак, а собаки могут загрызть гусей. Помогите фермеру построить по линиям сетки дополнительные заборы общей длины 30 м, чтобы защитить собак от гусей и гусей от собак.
Ответ: например, так, как на рисунке справа.
4)По кругу стоят 10 сорочат. Мама–сорока кормит их кашей: первому – 1 ложку, второму – 2 ложки, следующему – 1, потом – 2 и так далее. Всего она раздала 55 ложек каши, и на этом каша закончилась. Сколько сорочат получили ровно 4 ложки каши? Ответ нужно обосновать.
Ответ: 4 птенца
5)Никита записал два нечётных числа, а потом заменил в них разные цифры разными буквами, а одинаковые – одинаковыми. У Никиты получились два слова: УЧИТЕЛЯ и МЕЧТАТЕЛИ. Известно, что произведение цифр числа УЧИТЕЛЯ не равно нулю, а произведение цифр числа МЕЧТАТЕЛИ равно нулю. Чётной или нечётной будет сумма Я+И+МЕЧТА? Ответ нужно обосновать.
Ответ: чётная
6)В семье Веснушкиных три человека, и у каждого на лице в два раза больше веснушек, чем ему лет. Васе сейчас 11 лет. Васина мама младше Васиного папы на 3 года, и у неё на лице 66 веснушек. Сколько веснушек на лице у всех троих вместе? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 160 веснушек.
7)Найдите какое-нибудь решение неравенства М Ответ: например, М=1, А=3, Т=2, Е=4, И=5, К=9, т.е. 1
8)Маша попросила встать 30 одноклассников по кругу и стала раздавать им шоколадные конфеты. Первому дала 1 конфету, второму – 2 конфеты, следующему – снова 1 конфету, потом – 2 конфеты и так далее. Всего она раздала 55 конфет, и на этом конфеты закончилась. Сколько Машиных одноклассников получили ровно 2 конфеты? Ответ нужно обосновать
Ответ: 16 человек
9)На рисунке слева изображена фигура на клетчатой бумаге. Сторона каждой клетки равна 1 см. Разрежьте данную фигуру по линиям сетки на фигурки, удовлетворяющие всем четырём условиям: 1) площадь каждой равна 5 см2 ; 2) периметр каждой равен 12 см; 3) все фигурки должны быть различными, т.е. не совпадать при наложении; 4) в каждой должен быть ровно один серый квадратик. Достаточно привести один вариант разрезания.
Ответ: например, как на рисунке ниже.
10)Винни-Пух, Пончик и Карлсон приняли участие в турнире обжор. По результатам трёх туров судья заполнил таблицу, где указал, сколько пирогов в каждом туре съел каждый участник. Оказалось, что все числа в таблице различны. Ночью каждый из участников увеличил только один из своих результатов в таблице на 1. Утром все увидели следующую таблицу.
Ответ: см. файл выше
11)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
12)Мальвина написала на доске выражение М+А = Т+Е = М+А+Т = И+К+А и попросила Буратино заменить все буквы цифрами так, чтобы равенства оказались верными. Причем разные буквы нужно заменять разными цифрами, а одинаковые буквы ‒ одинаковыми цифрами. Помогите Буратино справиться с задачей. Достаточно привести хотя бы один пример.
Ответ: пусть М=5, А=2, Т=0, Е=7, И=1, К=4. Тогда получим верные равенства: 5+2=0+7=5+2+0=1+4+2.
13)Семи детям раздали 55 конфет. После этого первыйсказал, что по крайней мере 1 конфета у него имеется. «А у меня ровно на две больше!» — сказал второй. «А у меня ровно на две больше, чем у тебя!» — сказал третийвторому, затем такую же фразу произнес четвертый— третьему, пятый – четвертому, шестой— пятому. А седьмой заявил: «А у меня конфет больше всех!». Сколько конфет получил седьмой ребенок? Найдите все варианты и докажите, что других нет.
Ответ: 13 или 19
14)У Алисы есть три деревянных кубика. Длина ребра меньшего кубика равна 1 дм, среднего — 2 дм, большего — 3 дм. На покраску меньшего кубика ей потребовалось на 120 г краски меньше, чем на покраску среднего кубика. Сколько граммов краски ей потребуется на покраску большего кубика?
Ответ: 360 г.
15)Чтобы насытиться, голодному кролику нужно съесть ровно три каких-нибудь различных овоща. Какое наибольшее количество голодных кроликов можно накормить досыта, если в запасах имеется 5 кукуруз, 8 огурцов, 11 морковок и 17 перцев? Ответ нужно обосновать.
Ответ: 12
16)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
17)Замените буквы A, B, C, D, E, F, G, K цифрами от 1 до 8 без повторений так, чтобы числа 6, 11, 16, 21 в серых треугольниках являлись суммами цифр, стоящих в трёх белых треугольниках, соседствующих по сторонам с серым.
Ответ: подходящие значения букв: А=2, В=3, С=5, D=1, Е=8, F=4, G=6, К=7. Легко проверить, что условие задачи выполняется.
18)Рыбак поймал 6 кг рыбы. Часть приготовил себе, остальное отдал трём котам. Каждый кот съедает в 2 раза больше рыбы, чем рыбак за одно и то же время. Сколько килограммов рыбы было отдано котам, если есть все начали одновременно, а коты съели свою часть в 2 раза быстрее, чем рыбак?
Ответ: 4,5 кг.
19)Три одинаковых кубика приставлены друг к другу гранями с одинаковым числом очков. Найдите сумму чисел на трёх нижних гранях кубиков данной конструкции, на верхних гранях которых числа 3, 5 и 6.
Ответ: 7
20)Лиса Алиса, Буратино и Пьеро нашли 110 золотых монет. Алиса предложила разложить их на три кучки и сказала: «Пусть жребий определит, кому какая достанется!» Чтобы мальчики не расстраивались, они договорились уравнять свои кучки по меньшей, а лишнее отдать Алисе. (Например, если Буратино достанется 10 монет, Пьеро – 15, а Алисе – 85 монет, то Пьеро отдаст Алисе 5 монет, чтобы у него с Буратино стало поровну). Алисе необходимо разложить все монеты на три кучки так, чтобы в результате ей наверняка досталось не меньше 100 золотых монет. Сколько у нее есть вариантов?
Ответ: 15
21)Сколько раз в последовательности из 12 чисел: 2, _, _, _, _, _, _, _, _, _, _,1 (на первом месте стоит 2, на последнем месте 1) встретится цифра 2, если известно, что сумма любых трех чисел, идущих подряд, равна 5?
Ответ: 8 раз
22)На турнир «рыцарей и лжецов» математического кружка ребята мастерили из квадратного листа картона размером 150см×150см стену рыцарского замка. По краям и в середине было вырезано три одинаковых квадрата. Петя заметил, что при этом периметр первоначального листа увеличился на 8%. Найдите площадь получившейся «стены».
Ответ: 20772 см2
23)Петя и Вася живут в одном доме и выходят в школу одновременно. Петя сначала считает ворон и идет со скоростью 4 км/ч, но ровно на середине пути на парковке пересаживается на велосипед и едет со скоростью 12 км/ч. Вася идет в школу с постоянной скоростью и приходит в школу одновременно с Петей. Учитель Степан Иванович на середине пути обгоняет Петю на мопеде, так как его скорость в 5 раз больше скорости Васи, он приезжает в щколу на 3 минуты раньше мальчиков. Найдите расстояние от дома мальчиков до школы.
Ответ: 2км
24)По данным, изображенным на рисунке справа, найти длину катета BC прямоугольного треугольника АВС.
Ответ: 12
25)Какое наибольшее число «тетраминошек» (как на рисунке) можно разместить внутри квадрата 6×6 без наложений? Фигурки можно как угодно поворачивать и переворачивать.
Ответ: 8
26)Назовем прямоугольник «симпатичным», если его длинная сторона меньше удвоенной короткой. (В частности, квадрат является симпатичным прямоугольником). Разрежьте квадрат площади 100 на четыре симпатичных прямоугольника с площадями 10, 20, 30 и 40.
28)Винни-Пух заготовил мёд на зиму в нескольких полных горшочках по 5 литров каждый. Если бы он свои запасы мёда разлил в 4-литровые горшочки, то их потребовалось бы на четыре больше, правда, один горшочек оказался бы неполным. А если разлить весь мёд в горшочки по 7 литров, то их потребовалось бы на четыре меньше первоначального количества. Но один горшочек снова оказался бы неполным. Сколько горшочков мёда заготовил Винни-Пух?
29)Из вершин А, В и С треугольника АВС провели соответственно медиану АМ, биссектрису ВK и высоту СH. Оказалось, что середина отрезка ВK совпадает с серединой отрезка MH. Найдите углы треугольника АВС.
30)На каникулах для всех желающих провели турнир по шашкам. Каждый сыграл с каждым ровно одну партию. За победу в партии участник турнира получал 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Известно, что среди участников мальчиков было в десять раз больше, чем девочек, и они вместе набрали в 4,5 раза больше очков, чем девочки. Сколько очков набрала самая успешная девочка?
31)Девятиклассник Дима выписывает ряд последовательных трёхзначных чисел так, чтобы каждое число делилось нацело на свою последнюю цифру. Какое наибольшее количество чисел могло быть в этом ряду?
32)Имеется сталь двух сортов с содержанием никеля 55% и 12%. Сколько нужно взять металла каждого из сортов, чтобы получить 2021 т стали с содержанием 32% никеля?
33)Вася выписывает последовательность из 2021 натуральных чисел, начиная с некоторого числа, так, чтобы сумма любых трех подряд идущих чисел была равна 5. Какое наибольшее количество двоек у него может получиться?
34)На стороне ВС треугольника АВС выбрана точка F. Оказалось, что отрезок AF пересекает медиану BD в точке Е так, что АЕ = ВС. Докажите, что BF = FE.
35)Имеются две бочки с водой бесконечной вместимости и два ковшика объемами 2 и 2 2 литров. Можно ли, пользуясь этими ковшиками, перелить из одной бочки в другую ровно 1 литр?
36)От 2 кусков сплавов с разным содержанием свинца массой 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого сплава, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы отрезанных кусков?
37)Художник Петров красит плоскость в два цвета произвольным образом, а геометр Васильев утверждает, что сможет построить треугольник с вершинами одного цвета, величины углов которого относятся как 4:2:1. Прав ли он?
ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 1 Страница 67-73
Страница 67
Страница 68
2. Выполните действия. Используйте цветные полоски так, как это делали Волк и Заяц.
38 + 27 16 + 24 64 + 28
54 + 19 21 + 9 8 + 34
Ответ:
38 + 27 = 65
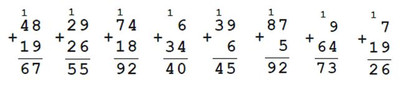
3. Вычисли, записывая решение столбиком.
48 + 19 74 + 18 39 + 6 9 + 64
26 + 29 6 + 34 87 + 5 7 + 19
Ответ:
5. Сколько истратили денег, если купили на 37 рублей колбасы и на 44 рубля сыра; банку майонеза за 47 рублей и сосисок на 48 рублей; пакет молока за 56 рублей и сыра на 35 рублей?
Ответ:
Если купили на 37 рублей колбасы и на 44 рубля сыра, то истратили:
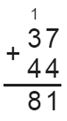
Если купили банку майонеза за 47 рублей и сосисок на 48 рублей, то истратили:
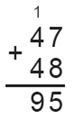
Если купили пакет молока за 56 рублей и сыра на 35 рублей, то истратили:
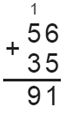
Страница 69
Страница 70
При сложении, чтобы узнать числа в окошках, нужно из суммы вычесть первое слагаемое.
Страница 71
16. Назови номера четырёхугольников.
Верно ли высказывание: «На рисунке есть пятиугольник и шестиугольник»?
Ответ:
Четырехугольники: 1, 3, 4
На рисунке есть пятиугольник под номером 6.
Шестиугольника нет.
17. Назови номера фигур, у которых 4 или 5 сторон.
Ответ:
1 фигура имеет 4 стороны.
3 фигура имеет 5 сторон.
Страница 72
20. Каждая из трёх девочек — Валя, Галя и Даша — держит один гладиолус: красный, белый или жёлтый. У Вали не красный и не белый, а у Гали не красный гладиолус. Какого цвета гладиолус у Даши?
Ответ:
Всего 3 гладиолуса: красный, белый и желтый.
Если У Вали не красный и не белый гладиолус, значит у нее желтый гладиолус.
Осталось 2 гладиолуса: красный и белый.
Если у Гали не красный гладиолус, значит у нее белый.
Остался один гладиолус: красный. Получается, красный гладиолус у Даши.
21. Из чисел 3, 15, 1, 10, 20, 7, 72, 21, 30, 48, 9, 17, 71, 100, 98 выпиши по порядку:
1) все однозначные числа, начиная с самого большого;
2) все двузначные числа, начиная с самого маленького.
Ответ:
1) 9, 7, 3, 1
2) 10, 15, 17, 20, 21,30, 48, 71, 72, 98
23. Вырази в сантиметрах.
5 дм 10 дм
1 дм 2 см 6 дм 6 см
9 дм 8 см 1 м
4 дм 4 см 2 дм 9 см
Ответ:
5 дм = 50 см
1 дм 2 см = 12 см
9 дм = 90 см
4 дм 4 см = 44 см
10 дм = 100 см
6 дм 6 см = 66 см
1 м = 100 см
2 дм 9 см = 29 см
Страница 73