для кодирования информации в компьютере используется система счисления
какая система счислений используется при кодировании информации в компьютере?
двоичная или бинарная (это одно и тоже)
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
01010111010100101010101001000001110110010101110101001010101010010000011101100101011101010010101010100100000111011
01010101011101011010010101010101001010100100101010001010101001010101001000101111010101001010100101010010100101001
Для кодирования информации в компьютере используется система счисления
Электронные облака
Лекции
Рабочие материалы
Тесты по темам
Template tips
Задачи
Логика вычислительной техники и программирования
Лекция «Системы счисления»
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Символы, при помощи которых записывается число, называются цифрами.
В конце концов, самой популярной системой счисления оказалась десятичная система. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э. В ней всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию несет не только цифра, но также и место позиция, на которой она стоит. В числе 444 три одинаковых цифры обозначают количество и единиц, и десятков, и сотен. А вот в числе 400 первая цифра обозначает число сотен, два 0 сами по себе вклад в число не дают, а нужны лишь для указания позиции цифры 4.
Классификация систем счисления
Системы счисления подразделяются на позиционные и непозиционные.
Позиционные системы счисления
Путем долгого развития человечество пришло к созданию позиционного принципа записи чисел, который состоит в том, что каждая цифра, содержащаяся в записи числа, занимает определенное место, называемое разрядом. Отсчет разрядов производится справа налево. Единица каждого следующего разряда всегда превосходит единицу предыдущего разряда в определенное число раз. Это отношение носит название основание системы счисления (у непозиционных систем счисления понятия «разряда» и «основания» отсутствуют).
Общее свойство всех позиционных систем счисления: при каждом переходе влево (вправо) в записи числа на один разряд величина цифры увеличивается (уменьшается) во столько раз, чему равно основание системы счисления.
Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. Например: Римская система счисления.
Из многочисленных представителей этой группы в настоящее время сохранила свое значение лишь римская система счисления, где для обозначения цифр используются латинские буквы:
| I | V | X | L | С | D | М |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
С их помощью можно записывать натуральные числа. Например, число 1995 будет представлено, как MCMXCV (М-1000,СМ-900,ХС-90 и V-5).
Правила записи чисел в римской системе счисления:
Например, запись XXX обозначает число 30, состоящее из трех цифр X, каждая из которых, независимо от места ее положения в записи числа, равна 10. Запись MCXX1V обозначает 1124, а самое большое число, которое можно записать в этой системе счисления, это число MMMCMXCIX (3999). Для записи еще больших чисел пришлось бы вводить все новые обозначения. По этой причине, а также по причине отсутствия цифры ноль, римская система счисления не годится для записи действительных чисел.
Таким образом, можно констатировать следующие основные недостатки непозиционных систем счисления:
Алфавит и основание системы счисления
Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например:
Десятичная система: <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>
Двоичная система: <0, 1>
Восьмеричная система: <0, 1, 2, 3, 4, 5, 6, 7>
Шестнадцатеричная система:
Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля.
Развёрнутая форма представления числа
Системы счисления, используемые в вычислительной технике
Несмотря на то, что исторически человек привык работать в десятичной системе счисления, с технической точки зрения она крайне неудобна, так как в электрических цепях компьютера требовалось бы иметь одновременно десять различных сигналов. Тем не менее, такие схемы существуют в некоторых видах микрокалькуляторов.
Чем меньше различных сигналов в электрических цепях, тем проще микросхемы, являющиеся основой конструкции большинства узлов ЭВМ, и тем надежнее они работают.
Наименьшее основание, которое может быть у позиционных систем счисления это – двойка. Именно поэтому двоичная система счисления используется в вычислительной технике, а двоичные наборы приняты за средство кодирования информации. В компьютере имеются только два устойчивых состояния работы микросхем, связанных с прохождением электрического тока через данное устройство (1) или его отсутствием (0). Говоря точнее, (1) кодирует высокое напряжение в схеме компьютера, а (0) – низкое напряжение.
Если вспомнить, что двоичная система счисления обладает самыми маленькими размерами таблиц сложения и умножения, то можно догадаться, что этот факт должен сильно радовать конструкторов ЭВМ, поскольку обработка сигнала в этом случае будет также самой простой. Таким образом, двоичная система счисления, с точки зрения организации работы ЭВМ, является наилучшей.
Мы уже говорили о преимуществах двоичной системы счисления с технической точки зрения организации работы компьютера. Зачем нужны другие системы счисления, кроме, естественно, еще и десятичной, в которой человек привык работать? Чтобы ответить на него, возьмем любое число в десятичной системе счисления, например 255, и переведем его в другие системы счисления с основаниями, кратными двойке:
Чем меньше основание системы счисления, тем больше разрядов требуется для его записи то есть, тем самым мы проигрываем в компактности записи чисел и их наглядности. Поэтому, наряду с двоичной и десятичной системами счисления, в вычислительной технике применяют так же запись чисел в 8-и 16-ричных системах счисления. Поскольку их основания кратны двойке, они органично связаны с двоичной системой счисления и преобразуются в эту систему наиболее быстро и просто (по сути они являются компактными видами записи двоичных чисел). Все другие системы счисления представляют для вычислительной техники чисто теоретический интерес.
Решение задач
1. Какое число записано с помощью римских цифр: CLVI
Решение: Зная обозначения, запишем: С – 100; L – 50; V – 5; I – 1
Решение: Пользуемся формулой:
a1 = 3; a2 = B; a3 = F; a4 = A
Следовательно: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*16 0
Ответ: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*160
3. Запишите в свёрнутой форме число 1*8 2 + 4*8 1 + 7*8 0
Решение: Пользуемся формулой:
Следовательно: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Ответ: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Алгоритмы перевода в системы счисления по разным основаниям
Алгоритм перевода чисел из любой системы счисления в десятичную
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую
Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую
Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую
Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2 n
Решение задач
1. Переведём в 10-ую с.с. число: 0,1235
Решение: Действуем строго по алгоритму перевода чисел из любой системы счисления в десятичную:
Найдём сумму ряда: 0,2 + 0,08 + 0,024 = 0,30410
Ответ: 0,1235 = 0,30410
2. Переведём число 12610 в 8-ую с.с. и число 18010 в 16-ую с.с.
Решение: Действуем строго по алгоритму перевода целых чисел из 10-ой с.с. в любую другую:
Во втором примере процесс можно продолжать бесконечно. В этом случае деление продолжаем до тех пор, пока не получим нужную точность представления. Записываем числа сверху вниз.
Ответ: 0,6562510 = 0,А816; 0,910 = 1,1110012 с точностью до семи значащих цифр после запятой.
4. Переведём число 124,2610 в шестнадцатеричную с.с.
Решение: Действуем строго по алгоритму перевода произвольных чисел:
Переводим целую и дробную часть:
Записываем полученные числа справа налево (в целой части) и сверху вниз (в дробной части).
Ответ: 124,2610 = 7С,428А16
5. Переведём число: 11001010011010101112 в шестнадцатеричную систему счисления
Решение: Действуем строго по алгоритму перевода чисел из 2-ой с.с в с.с. с основанием 2 n :
Для кодирования информации в компьютере используется система счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятк ов, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Кодирование информации — основные виды, способы и правила
Информация бывает разных видов, таких как запах, вкус, звук; символы и знаки. В различных отраслях науки, техники и культуры применяются особые формы и методики для кодирования и записи информации.
Рассмотрим, например, персональные компьютеры, которые предназначены для обработки графических изображений, воспроизведения музыки и видеофайлов, организации видео конференций, научных расчетов. Для предоставления данных в виде, понимаемом компьютерами, проводится кодирование информации путём составления специальной модели явления либо объекта. Именно процесс преобразования сообщения в комбинацию символов называется кодированием.
Системы счисления делятся на позиционные и непозиционные. Пример непозиционной системы счисления — римская: несколько чисел приняты за основные (например, I, V, X, L, C, D, M), а остальные получаются из основных путем сложения (как VI, VII) или вычитания (как IV, IX). В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
Трактовка понятий
Человеческие мысли выражаются в виде текста, который состоит из слов. Подобное представление информации называется алфавитным, так как основа языка — алфавит. Он считается конечным набором различных знаков любой природы. Их используют для составления сообщений.
Вам известно что для обозначения количества мы пользуемся цифрами, для обозначения звуков на письме буквами. Можно сказать что цифры и буквы это коды. Одна и тажа информация может быть закодирована по разному. Например китайские и японские иероглифы являются символами которыми кодируется буква или слово. Основу любого языка составляет алфавит — конечный набор различных знаков (символов) любой природы, из которых складывается сообщение на данном языке. То есть символизация информации – это описание объектов или явлений с помощью символов того или иного алфавита. Под мощностью алфавита понимают количество символов, составляющий данный алфавит, что в свою очередь определяет количество возможных комбинаций (слов) которые можно составить из символов данного алфавита в соответствии с определенными правилами.
Как правило представления сообщения, подбираются так что бы его передача была как можно быстрее и надежней, а его обработка была как можно более удобной для адресата. Одно и тоже сообщение можно кодировать по разному. Одной систем кодирования является азбука. Можно кодировать и звуки одна из таких систем кодирования — ноты. Хранить можно не только текстовую и звуковую информацию, в виде кодов хранятся и изображения. Если рассмотреть рисунок через увеличительное стекло то видно что он состоит из точек. Координаты каждой точки можно запомнить в виде чисел. Цвет каждой точки можно запомнить так же в виде чисел. Такие числа могут храниться в памяти компьютера и передаваться на расстояния.
Чтобы зашифровать данные, необходимо знать правила записи кодов (условные обозначения информации). Понятие кодирование связано с преобразованием сообщений в комбинацию символов с учётом кодов. При общении люди используют русский либо другой национальный язык. В процессе разговора код передаётся звуками, а при письменном общении с помощью букв. У водителей или у пилотов обработка информации также осуществляется световыми сигналами, специальнвми символами — знаками.
Количество и графическое отображение символов в алфавитах естественных языков сложилось исторически и характеризуется особенностями языка (произносимыми звуками). Например русский алфавит имеет 33 символа, латинский – 26, китайский несколько тысяч.
К основным способам кодирования информации в информатике относятся: числовой, символьный (текстовый), графический. В первом случае используются числа, во втором — символы того алфавита, что и первоначальный текст, в третьем — картинки, рисунки, значки.
Двоичная методика
Современный компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео информацию. В процессе хранения, обработки и передачи информации в компьютере используется особая двоичная система кодирования, алфавит которой состоит всего из двух знаков «0» и «1». Дело в том, что компьютер способен обрабатывать и хранить только лишь один вид представления данных – цифровой. Связано это с тем, что в цифровой электронике удобнее всего представлять информацию в виде последовательности электрических импульсов: техническое устройство, безошибочно различающее 2 разных состояния сигнала, оказалось проще создать, чем то, которое бы безошибочно различало 5 или 10 различных состояний. Поэтому любую входящую в него информацию необходимо переводить в цифровой вид. Такое кодирование информации принято называть двоичным, на его основе работают все окружающие нас компьютеры, смартфоны и т.п.
На английском языке используется выражение binary digit либо сокращённо bit (бит). Через 1 бит можно выразить: да либо нет; белое или чёрное; ложь либо истина.
Двоичное кодирование информации привлекает тем, что легко реализуется технически. Электронные схемы для обработки двоичных кодов должны находиться только в одном из двух состояний: есть сигнал/нет сигнала или высокое напряжение/низкое напряжение. В результате любая информация кодируется в компьютерах с помощью последовательностей лишь двух цифр — 0 и 1.
Итак, минимальные единицы измерения информации – это бит и байт. Один бит позволяет закодировать 2 значения (0 или 1). Используя два бита, можно закодировать 4 значения: 00, 01, 10, 11. Тремя битами кодируются 8 разных значений: 000, 001, 010, 011, 100, 101, 110, 111. Из приведенных примеров видно, что добавление одного бита увеличивает в 2 раза то количество значений, которое можно закодировать. 1 байт состоит из 8 бит и способен закодировать 256 значений.
Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту. Поэтому чаще всего одному символу текста, хранимому в компьютере, соответствует один байт памяти.
Наряду с битами и байтами используют и большие единицы измерения информации.
Подробнее о информации в компьютерных системах можно прочтитать в статье Понятие информации. Информатика
Текстовое значение
Кодирование и обработка текстовой информации Уже с 60-х годов прошлого столетия, компьютеры всё больше стали использовать для обработки текстовой информации. Для кодирования текстовой информации в компьютере применяется двоичное кодирование, т.е. представление текста в виде последовательности 0 и 1. Чтобы выразить текст числом, каждая буква сопоставляется с числовым значением. Смысл кодирования: одному символу принадлежит код в пределах 0−255 либо двоичный код от 00000000 до 11111111.
Текстовая информация состоит из символов: букв, цифр, знаков препинания и др. Одного байта достаточно для хранения 256 различных значений, что позво ляет размещать в нем любой из алфавитно-цифровых символов. Первые 128 сим волов (занимающие семь младших бит) стандартизированы с помощью кодировки ASCII (American Standart Code for Information Interchange). Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 0000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
В мировой практике для кодирования текста при помощи байтов используются разные стандарты. Самым распространенным, но не единственным видом кодирования является код ASCII. В соответствии с этим стандартом, знаки в пределах 0−32 соответствуют операциям, а 33−127 — символам из латинского алфавита, знакам препинания и арифметики. Для национальных кодировок применяются значения 128−255. В разных национальных кодировках одному и тому же коду соответствуют различные символы. К примеру, существует 5 кодировочных таблиц для русских букв (Windows, MS-DOS, Mac, ISO, КОИ – 8). Поэтому тексты созданные в одной кодировке не будут правильно отображаться в другой.
Первоначально в кодах ASCII было 7 бит информации. В последующем ее расширили до 8-битной (1 байт) кодировки. Обьем 7-битного кодирования по сравнению с 8-битным в 2 раза меньше. 2 7 =128 8 =256.
В настоящее время для кодирования кириллицы наибольшее распространение получила кодовая таблица СР1251, которая используется в операционных системах семейства Windows фирмы Microsoft. Во всех современных кодовых таблицах, кроме таблицы стандарта Unicode, для кодирования одного символа отводится 8 двоичных разрядов (8 бит).
В конце прошлого века появился новый международный стандарт Unicode, в котором один символ представляется двухбайтовым двоичным кодом. Применение этого стандарта – продолжение разработки универсального международного стандарта, позволяющего решить проблему совместимости национальных кодировок символов. С помощью данного стандарта можно закодировать 65536 различных символов.
Растровое изображение
Графическая информация, представленная в виде рисунков, фотографий, слайдов, подвижных изображений (анимация, видео), схем, чертежей, может создаваться и редактироваться с помощью компьютера, при этом она соответствующим образом кодируется. В настоящее время существует достаточно большое количество прикладных программ для обработки графической информации, но все они реализуют три вида компьютерной графики: растровую, векторную и фрактальную. Мы рассмотрим самую распространенный, растровый формат кодирования изображения.
Графические данные на мониторе представляются в качестве растрового изображения. Если более пристально рассмотреть графическое изображение на экране монитора компьютера, то можно увидеть большое количество разноцветных точек (пикселов – от англ. pixel, образованного от picture element – элемент изображения), которые, будучи собраны вместе, и образуют данное графическое изображение. Каждому пикселю присвоен особый код, в котором хранится информация об оттенке пикселя. Из этого можно сделать вывод: графическое изображение в компьютере определенным образом кодируется и должно быть представлено в виде графического файла.
Файлы, созданные на основе растровой графики, предполагают хранение данных о каждой отдельной точке изображения. Для отображения растровой графики не требуется сложных математических расчетов, достаточно лишь получить данные о каждой точке изображения (ее координаты и цвет) и отобразить их на экране монитора компьютера.
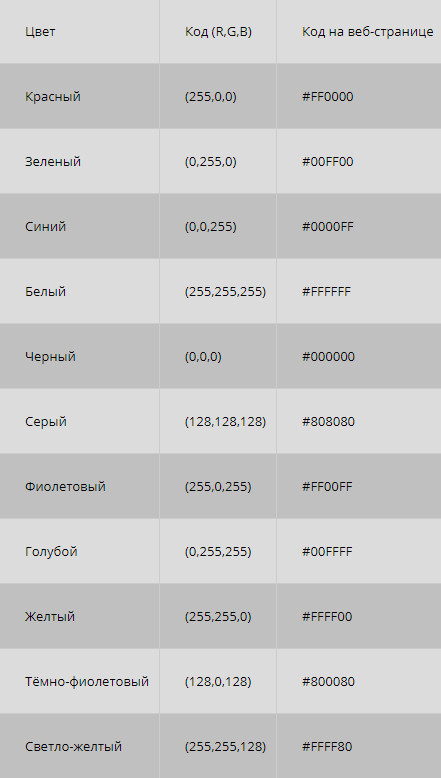
Что делать, если рисунок цветной? Формирование цветного изображения на мониторе осуществляется путём смешивания 3-х основных цветов: синего, красного и зелёного. В этом случае для кодирования цвета пикселя уже не обойтись одним битом. В системе кодирования цветных изображений RGB (R — красный, G — зеленый и B — синий) яркость каждой цветовой составляющей (или, как говорят, каждого канала) кодируется целым числом от 0 до 255. При этом код цвета — это тройка чисел (R,G,B), яркости отдельных каналов. Цвет (0,0,0) — это черный цвет, а (255,255,255) — белый. Если все составляющие имеют равную яркость, получаются оттенки серого цвета, от черного до белого. При кодировании цвета на веб-страницах также используется модель RGB, но яркости каналов записываются в шестнадцатеричной системе счисления (от 0016 до FF16), а перед кодом цвета ставится знак #. Например, код красного цвета записывается как #FF0000, а код синего — как #0000FF.
Звуки и их разрядность
Человек воспринимает звуковые волны (колебания воздуха) с помощью слуха в форме звука различных громкости и тона. Чем больше интенсивность звуковой волны, тем громче звук, чем больше частота волны, тем выше тон звука. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, для каждого такого участка устанавливается определенная величина интенсивности звука.
В каждом современном компьютере предусмотрена звуковая плата, колонки, микрофон. С их помощью производится запись, сохраняются и воспроизводятся звуки — волны с определённой частотой и амплитудой. Программное обеспечение для компьютеров преобразовывает звуковые сигналы в последовательность нулей и единиц. Для этого использунтся аудиоадаптер или звуковая плата. Устройство подключается к компьютеру с целью преобразования электроколебаний звуковой частоты в двоичный код. Процесс преобразования выполняется как при вводе звуков в компьютер так и при обратном их преобразовании.
Для человека звук тем громче, чем больше амплитуда сигнала, и тем выше тон, чем больше частота сигнала. Компьютер — устройство цифровое, поэтому непрерывный звуковой сигнал должен быть преобразован в последовательность электрических импульсов (нулей и единиц). Оцифровку звука выполняет специальное устройство на звуковой плате. Называется оно аналого-цифровой преобразователь (АЦП). Обратный процесс — воспроизведение закодированного звука производится с помощью цифро-аналогового преобразователя (ЦАП).
В процессе кодирования непрерывного звукового сигнала производится его дискретизация по времени, или, как говорят, «временная дискретизация».
Для записи аналогового звука и г го преобразования в цифровую форму используется микрофон, подключенный к звуковой плате. Качество полученного цифрового звука зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее «лесенка» цифрового звукового сигнала повторяет кривую аналогового звукового сигнала.
Глубина кодирования звука — это количество бит, используемое для кодирования различных уровней сигнала или состояний. Современные звуковые карты обеспечивают 16-битную глубину кодирования звука, и тогда общее количество различных уровней громкомти, который сможет распознать компьютер будет: N = 2 16 = 65536.
Частота дискретизации- это количество измерений уровня звукового сигнала в единицу времени. Эта характеристика показывает качество и точность процедуры двоичного кодирования. Измеряется в герцах (Гц).
Одно измерение за одну секунду соответствует частоте 1 Гц, 1000 измерений за одну секунду — 1 килогерц (кГц). Частота дискретизации звукового сигнала может принимать значения от 8 до 196 кГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц — качеству звучания аудио-CD. Достаточно высокое качество звучания достигается при частоте дискретизации 44 кГц и глубины кодирования звука, равной 16 бит.
Оцифрованный сигнал в виде набора последовательных значений амплитуды уже можно сохранить в памяти компьютера. В случае, когда записываются абсолютные значения амплитуды, такой формат записи называется PCM ( Pulse Code Modulation). Стандартный аудио компакт-диск (CD-DA), применяющийся с начала 80-х годов 20-го столетия, хранит информацию в формате PCM с частотой дискретизации 44.1 кГц и разрядностью квантования 16 бит.
Подробнее о свойствах звука можно прочитать в статье Звук
Машинные команды
В вычислительных машинах, включая компьютеры, предусмотрена программа для управления их работой. Все команды кодируются в определённой последовательности с помощью нулей и единиц. Подобные действия называются машинными командами (МК).
Машинная команда представляет собой закодированное по определенным правилам указание микропроцессору на выполнение некоторой операции или действия. Каждая команда содержит элементы, определяющие:
Структура машинной команды состоит из операционной и адресной части. В операционной части содержится код операции. Чем длиннее операционная часть, тем большее количество операций можно в ней закодировать.
В адресной части машинной команды содержится информация об адресах операндов. Это либо значения адресов ячеек памяти, в которых размещаются сами операнды (абсолютная адресация), либо информация, по которой процессор определяет значения их адресов в памяти (относительная адресация). Абсолютная адресация использовалась только в машинах 1 и 2-го поколений. Начиная с машин 3-го поколения, наряду с абсолютной используется относительная адресация.
Подробнее о поколениях компьютеров смотрите в статье История развития компьютеров
Заключение
Итак, кодирование информации — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки (Цифровое кодирование, аналоговое кодирование, таблично-символьное кодирование, числовое кодирование). Процесс преобразования сообщения в комбинацию символов в соответствии с кодом называется кодированием, процесс восстановления сообщения из комбинации символов называется декодированием.
Кодирование информации — процесс формирования определенного представления информации. В более узком смысле под термином «кодирование» понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.
Информацию необходимо представлять в какой — либо форме, т.е. кодировать. Для представления дискретной информации используется некоторый алфавит. Однако однозначное соответствие между информацией и алфавитом отсутствует. Другими словами, одна и та же информация может быть представлена посредством различных алфавитов. В связи с такой возможностью возникает проблема перехода от одного алфавита к другому, причём, такое преобразование не должно приводить к потере информации.