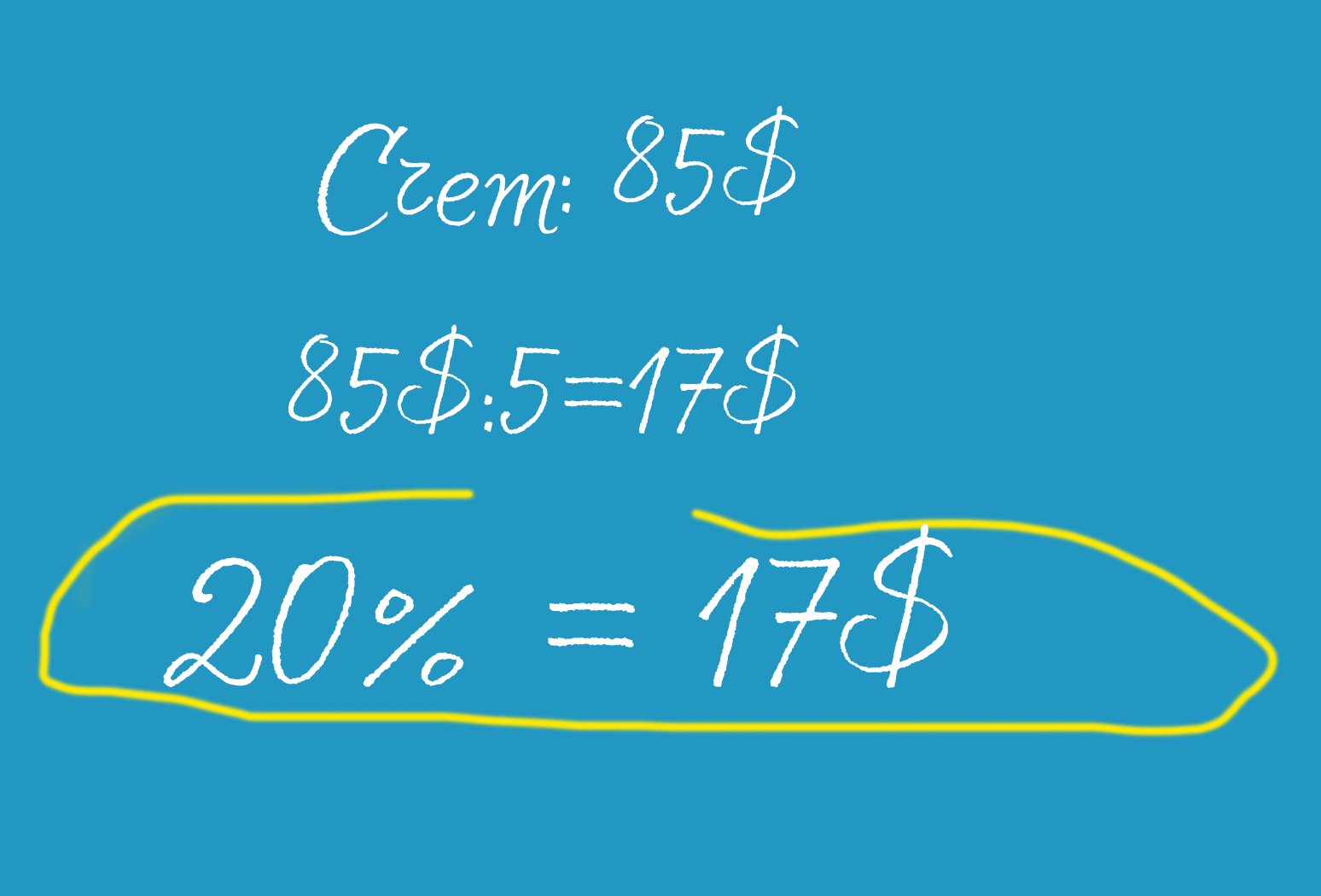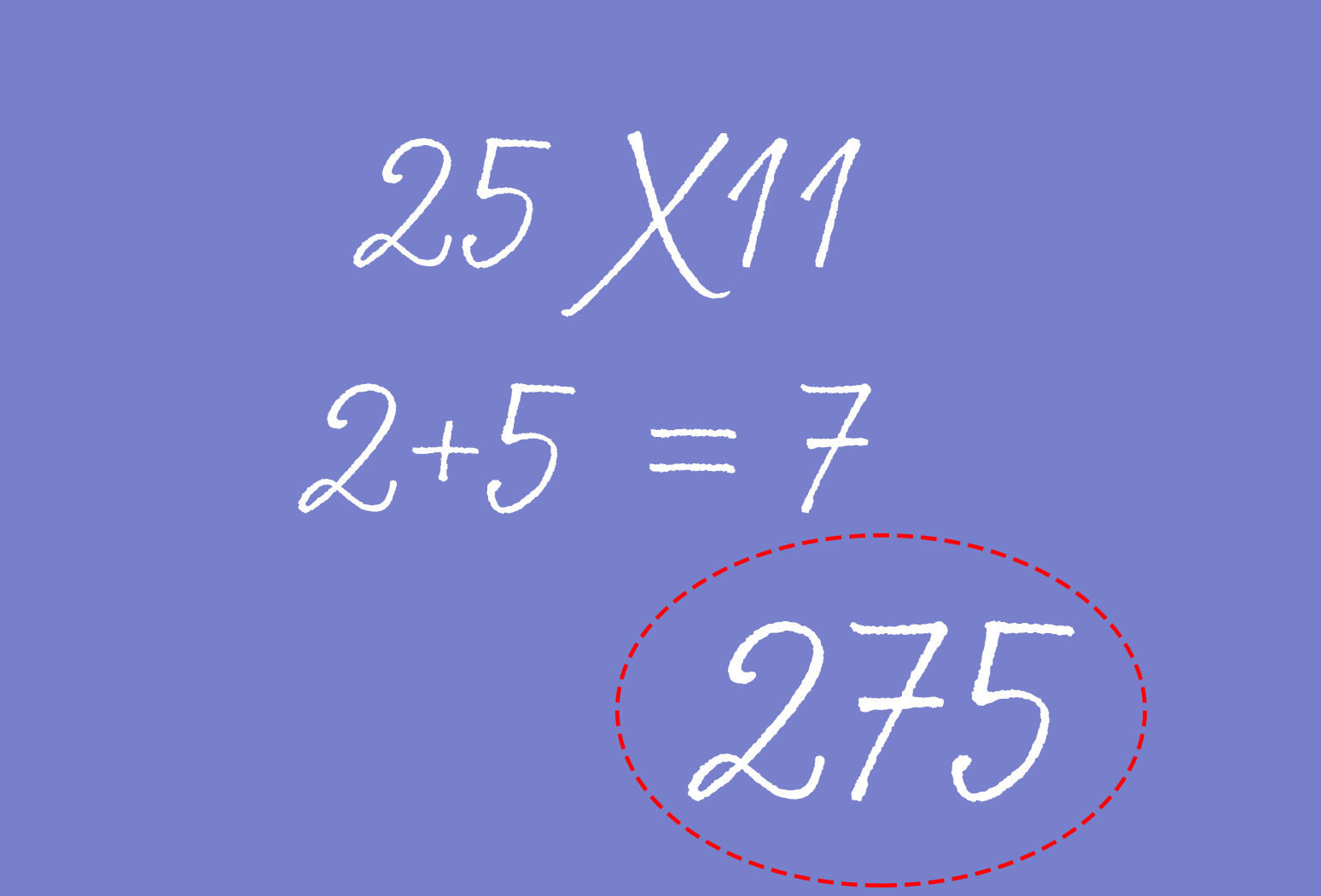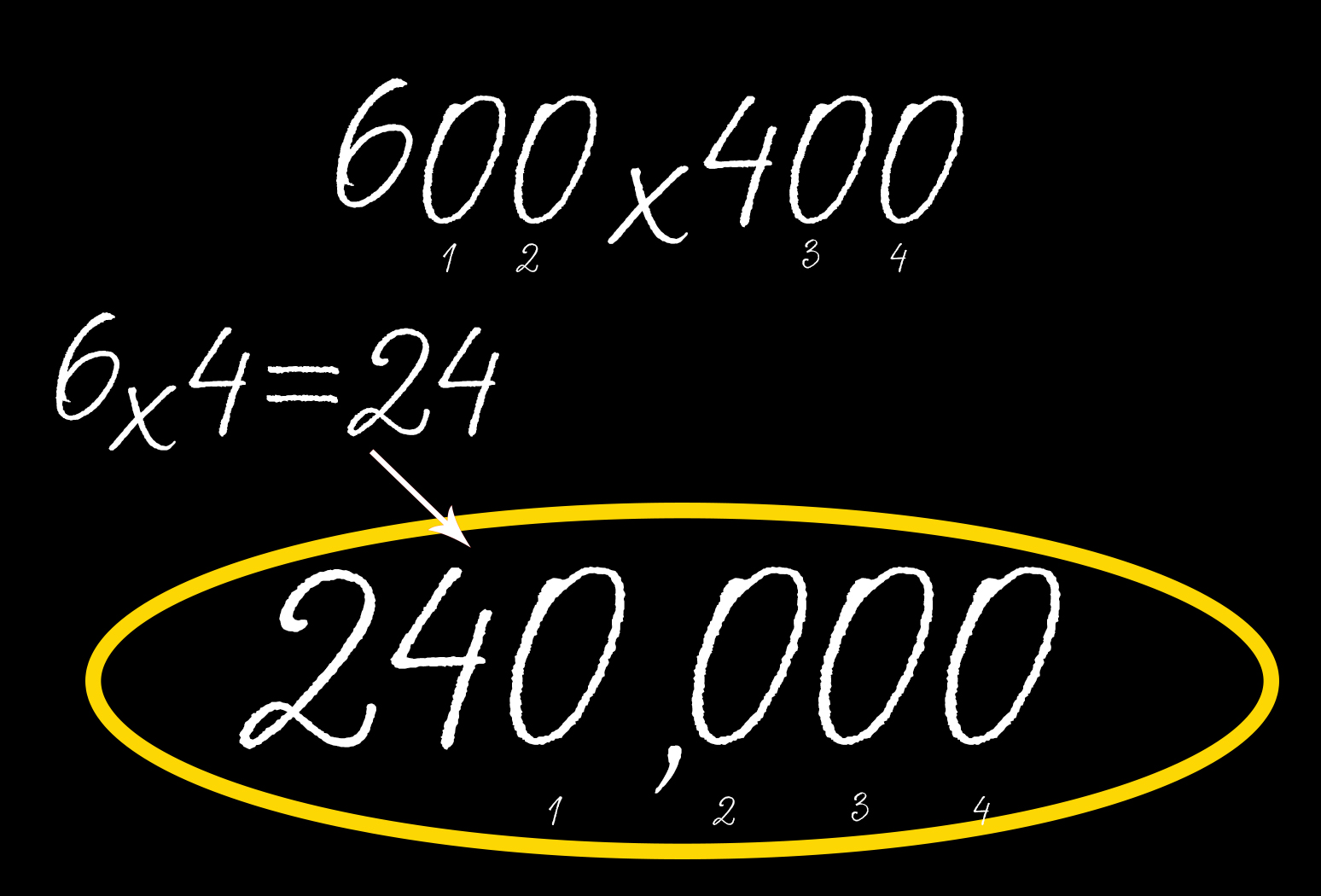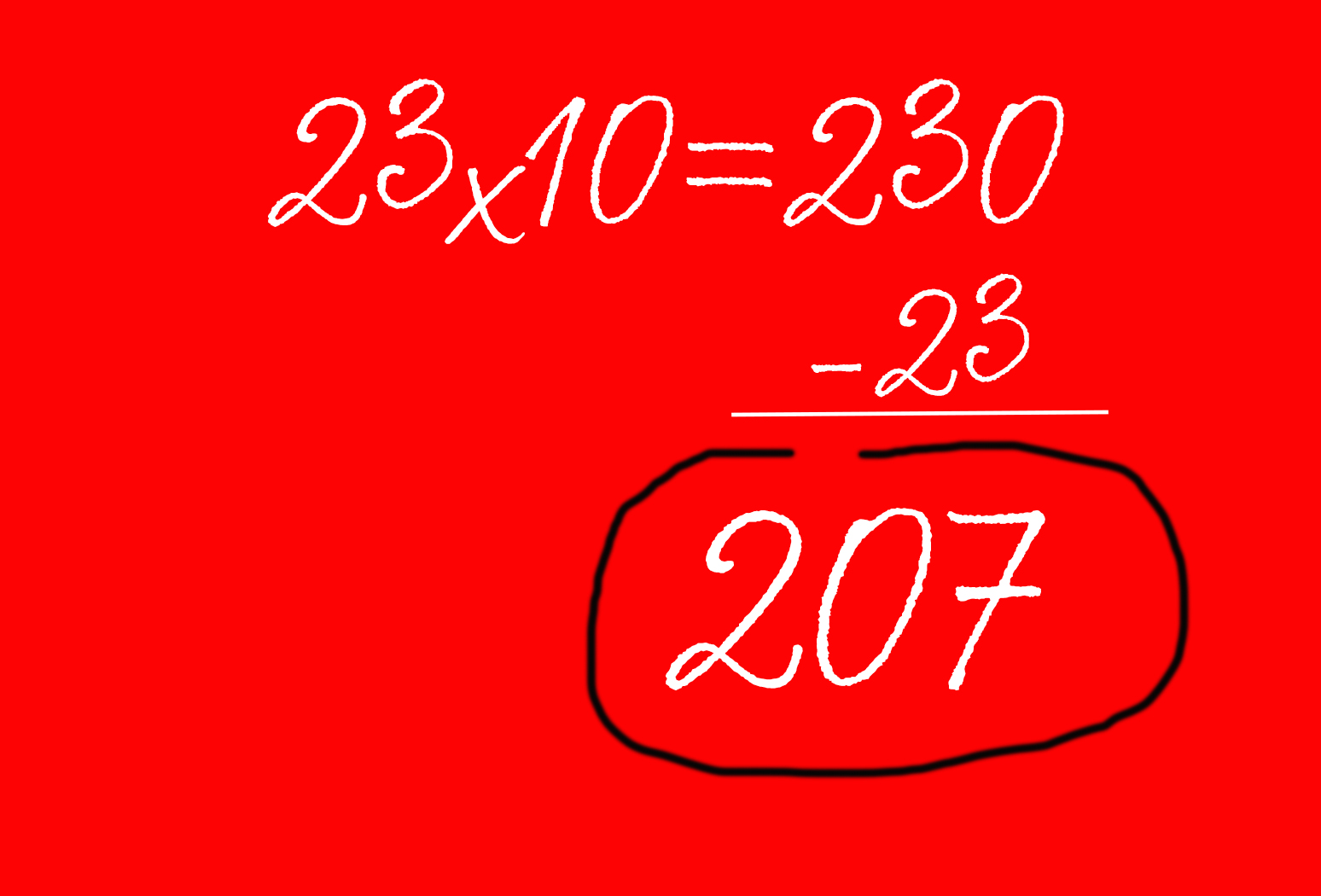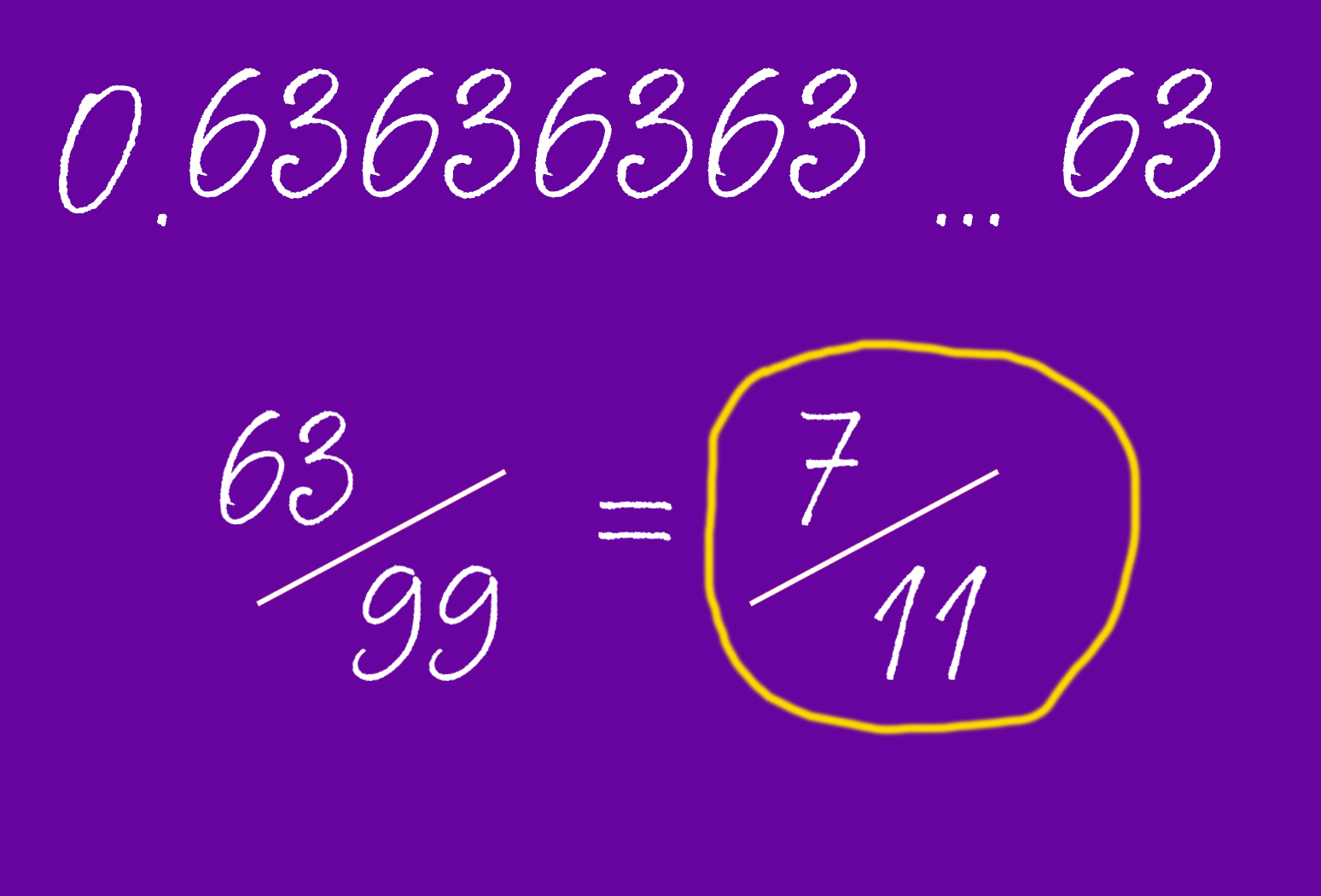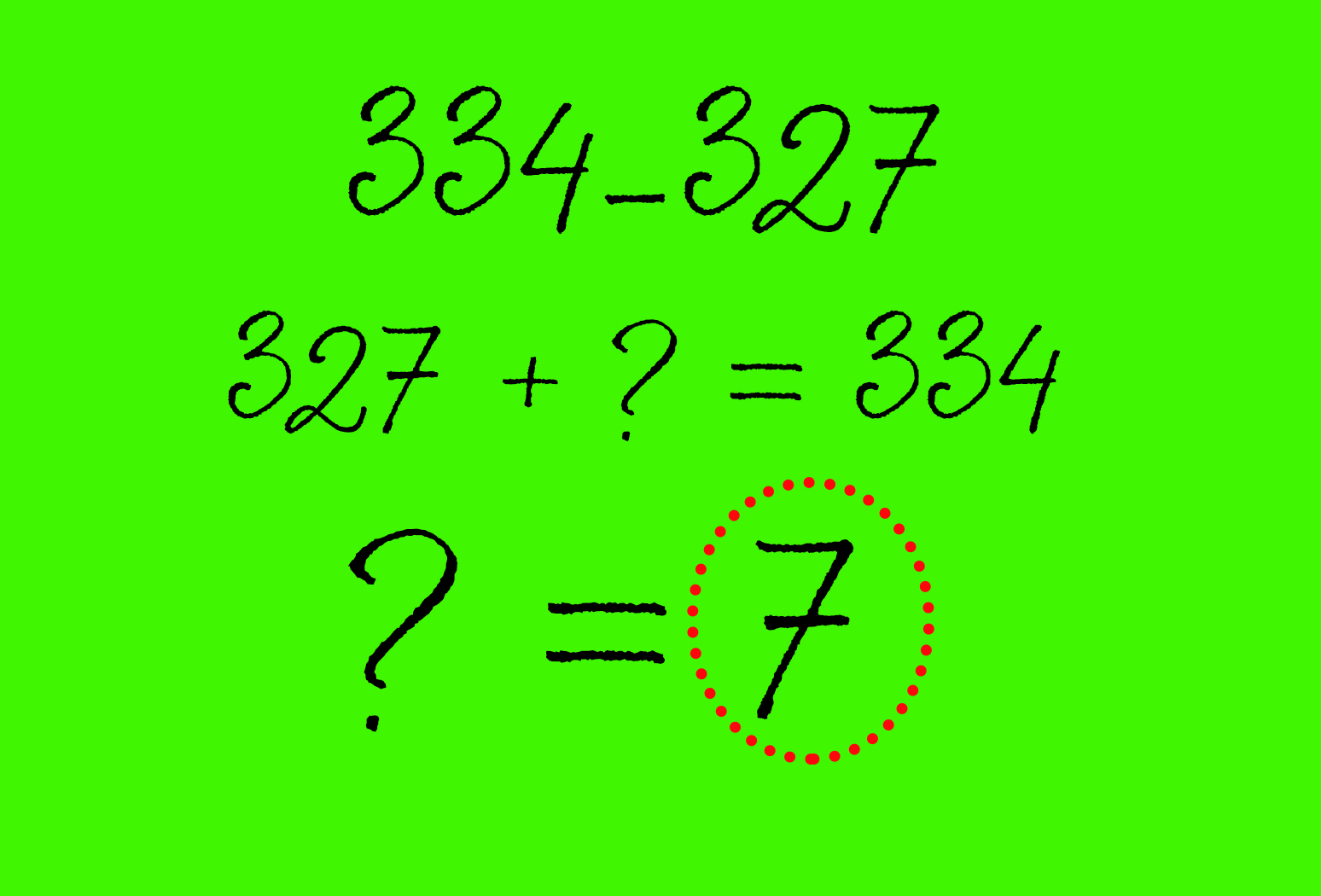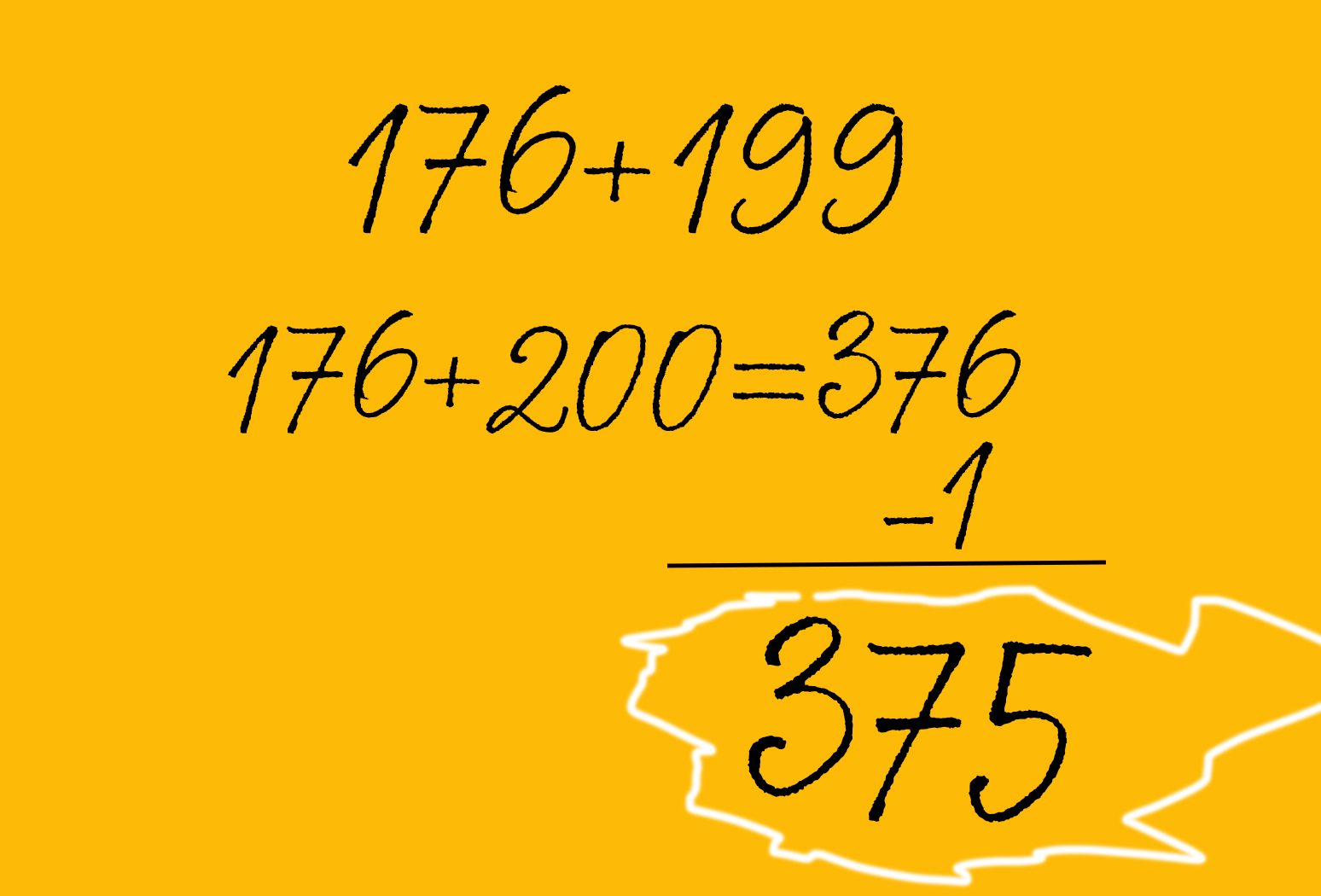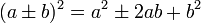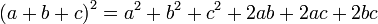как быстро возвести число в степень без калькулятора в уме

Быстрое возведение чисел в квадрат без калькулятора

Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.

Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:

1156 — это и есть квадрат 34.

Проблему данного способа можно описать двумя пунктами:

1) он требует письменного оформления;

2) в процессе вычисления очень легко допустить ошибку.

Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.

Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:

Например, 28 можно представить в следующем виде:

Аналогично представляем оставшиеся примеры:

Аналогично выбираем варианты и для остальных примеров:

Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:

Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.

Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.

Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:

Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:

И так со всеми числами, отличающимися на единицу.

Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:

Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:

При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.

Ключевые моменты

С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!

Для начала запомните квадраты значений, кратных 10:

Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:

Как считать еще быстрее

Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:

Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:

— это и есть формула.

— аналогичная формула для чисел, больших на 1.

Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!

Источник

Быстрое возведение чисел от 1 до 100 в квадрат

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.

В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.

В таблице отмечены зеленым.

Правило 3 (отсекает 8 чисел)

Для чисел от 40 до 50.

Достаточно трудно, верно? Давайте разберем пример:

В таблице отмечены светло-оранжевым.

Правило 4 (отсекает 8 чисел)

Для чисел от 50 до 60.

Тоже достаточно трудно для восприятия. Давайте разберем пример:

В таблице отмечены темно-оранжевым.

Правило 5 (отсекает 8 чисел)

Для чисел от 90 до 100.

Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:

В таблице отмечены темно-темно-оранжевым.

Правило №6 (отсекает 32 числа)

Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.

Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:

Формулы (осталось 24 числа)

Для чисел от 25 до 50

Для чисел от 50 до 100

Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):

UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:

Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».

Для квадратов, соответственно, еще проще.

Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.

Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Источник

Красота чисел. Как быстро вычислять в уме

Старинная запись на квитанции в уплате подати («ясака»). Она означает сумму 1232 руб. 24 коп. Иллюстрация из книги: Яков Перельман «Занимательная арифметика»

Ещё Ричард Фейнман в книге «Вы конечно шутите, мистер Фейнман!» поведал несколько приёмов устного счёта. Хотя это очень простые трюки, они не всегда входят в школьную программу.

Например, чтобы быстро возвести в квадрат число X около 50 (50 2 = 2500), нужно вычитать/прибавлять по сотне на каждую единицы разницы между 50 и X, а потом добавить разницу в квадрате. Описание звучит гораздо сложнее, чем реальное вычисление.

52 2 = 2500 + 200 + 4
47 2 = 2500 – 300 + 9
58 2 = 2500 + 800 + 64

Молодого Фейнмана научил этому трюку коллега-физик Ханс Бете, тоже работавший в то время в Лос-Аламосе над Манхэттенским проектом.

Ханс показал ещё несколько приёмов, которые использовал для быстрых вычислений. Например, для вычисления кубических корней и возведения в степень удобно помнить таблицу логарифмов. Это знание очень упрощает сложные арифметические операции. Например, вычислить в уме примерное значение кубического корня из 2,5. Фактически, при таких вычислениях в голове у вас работает своеобразная логарифмическая линейка, в которой умножение и деление чисел заменяется сложением и вычитанием их логарифмов. Удобнейшая вещь.

Логарифмическая линейка

До появления компьютеров и калькуляторов логарифмическую линейку использовали повсеместно. Это своеобразный аналоговый «компьютер», позволяющий выполнить несколько математических операций, в том числе умножение и деление чисел, возведение в квадрат и куб, вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени. Точность расчётов — около 3 значащих цифр.

Чтобы быстро проводить в уме сложные расчёты даже без логарифмической линейки, неплохо запомнить квадраты всех чисел, хотя бы до 25, просто потому что они часто используются в расчётах. И таблицу степеней — самых распространённых. Проще запомнить, чем вычислять каждый раз заново, что 5 4 = 625, 3 5 = 243, 2 20 = 1 048 576, а √3 ≈ 1,732.

Ричард Фейнман совершенствовал свои навыки и постепенно замечал всё новые интересные закономерности и связи между числами. Он приводит такой пример: «Если кто-то начинал делить 1 на 1,73, можно было незамедлительно ответить, что это будет 0,577, потому что 1,73 — это число, близкое к квадратному корню из трёх. Таким образом, 1/1,73 — это около одной трети квадратного корня из 3».

Настолько продвинутый устный счёт мог бы удивить коллег в те времена, когда не было компьютеров и калькуляторов. В те времена абсолютно все учёные умели хорошо считать в уме, поэтому для достижения мастерства требовалось достаточно глубоко погрузиться в мир цифр.

В наше время люди достают калькулятор, чтобы просто поделить 76 на 3. Удивить окружающих стало гораздо проще. Во времена Фейнмана вместо калькулятора были деревянные счёты, на которых тоже можно было производить сложные операции, в том числе брать кубические корни. Великий физик уже тогда заметил, что использование таких инструментов, людям вообще не нужно запоминать множество арифметический комбинаций, а достаточно просто научиться правильно катать шарики. То есть люди с «расширителями» мозга не знают чисел. Они хуже справляются с задачами в «автономном» режиме.

Вот пять очень простых советов устного счёта, которые рекомендует Яков Перельман в методичке «Быстрый счёт» 1941 года издательства.

1. Если одно из умножаемых чисел разлагается на множители, удобно бывает последовательно умножать на них.

225 × 6 = 225 × 2 × 3 = 450 × 3
147 × 8 = 147 × 2 × 2 × 2, то есть трижды удвоить результат

2. При умножении на 4 достаточно дважды удвоить результат. Аналогично, при делении на 4 и 8, число делится пополам дважды или трижды.

3. При умножении на 5 или 25 число можно разделить на 2 или 4, а затем приписать к результату один или два нуля.

Здесь лучше сразу оценивать, как проще. Например, 31 × 25 удобнее умножать как 25 × 31 стандартным способом, то есть как 750+25, а не как 31 × 25, то есть 7,75 × 100.

При умножении на число, близкое к круглому (98, 103), удобно сразу умножить на круглое число (100), а затем вычесть/прибавить произведение разницы.

37 × 98 = 3700 – 74
37 × 104 = 3700 + 148

4. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (9), и приписывают 25.

8 × 9 = 72, приписываем 25, так что 85 2 = 7225

Почему действует это правило, видно из формулы:

(10Х + 5) 2 = 100Х 2 + 100Х + 25 = 100Х (X+1) + 25

Приём применяется и к десятичным дробям, которые оканчиваются на 5:

5. При возведении в квадрат не забываем об удобной формуле

(a + b) 2 = a 2 + b 2 + 2ab
44 2 = 1600 + 16 + 320

Источник

Долой калькулятор: 12 простых трюков, которые помогут вам быстро считать

Просто, как дважды два.

Как бы мы ни хотели это признавать, учителя были правы: математика нужна каждому из нас. Но далеко не всем дается ловкое жонглирование числами. Тогда на помощь приходят легко запоминающиеся математические приемы – настоящее спасение, когда под рукой, как назло, нет калькулятора.

Ниже вы найдете 12 способов быстрых вычислений для всех, кто далек от точных наук.

1. Быстрое вычисление 20%

Представим, что границы вновь открыли и первым делом вы отправились в США. А там принято оставлять на чай. Обычно размер чаевых составляет 15-20% от суммы вашего заказа.

По словам Кейт Сноу, автора серии книг The Math Facts That Stick, чтобы быстро вычислить 20% от суммы, вам нужно просто разделить число в чеке на 5.

Например, вы поели на 85 долларов. Разделите 85 на 5, и у вас получится 17 долларов – чаевые, которые вы должны оставить официанту.

2. Умножение двузначных чисел на 11

Умножить число на 11 очень легко с помощью хитрого трюка от math.hmc.edu. Просто сложите две цифры и поместите полученную сумму в середину числа.

Например, вы умножаете 25 на 11. Если сложить 2 и 5, получится 7. Теперь расположите 7 между 2 и 5, чтобы найти окончательный ответ – 275.

3. Быстрое удвоение

Чтобы удвоить большое число, умножьте каждую цифру на 2 и сложите их между собой. Кейт Сноу предлагает начинать слева – так будет легче.

«Чтобы удвоить, к примеру, 147, начните с разряда сотен. Если умножить 100 на 2, получится 200. 40 на 2 – 80. 7 на 2 – 14. Теперь сложите числа между собой (200 + 80 + 14), и вы получите 294», – объясняет Сноу.

4. Умножение чисел, которые оканчиваются на ноль

Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.

Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.

5. Умножение на 9

Если вам так и не удалось выучить таблицу умножения – не переживайте. По словам Сноу, чтобы легко умножить число на 9, нужно умножить его на 10 и вычесть исходное число из полученного значения.

Например, вам нужно умножить 9 на 23. Для этого умножаем 23 на 10 и получаем 230. А затем вычитаем из него 23, чтобы получить окончательный ответ – 207.

6. Деление на 10, 100 или 1000

Разделить число на 10 проще простого – согласно Сноу, «нужно просто переместить десятичный знак на одну позицию влево от исходного числа, чтобы найти ответ».

Для деления на 100 применим тот же метод, за исключением одного – нужно переместить десятичный разряд на две позиции левее исходного числа. Что касается деления на 1000, просто переместите десятичный знак на три позиции влево.

Например, если вы делите 42,94 на 10, вы просто перемещаете десятичный знак на одну позицию влево и получаете 4,294.

7. Умножение на 10, 100 или 1000

Здесь все работает с точностью до наоборот. Чтобы умножить число на 10, переместите десятичный знак на одну позицию вправо. На 100 – на две позиции. На 1000 – на три позиции.

Например, если вам нужно умножить 366,78 на 100, передвиньте десятичный знак на две цифры вправо, чтобы получить ответ 36678.

8. Преобразование периодической десятичной дроби в обыкновенную

Согласно businessinsider.com, нужно выполнить всего 3 шага, чтобы легко превратить бесконечную десятичную дробь в обыкновенную, с числителем и знаменателем.

9. Умножение на 25

Умножать на 25 не так уж и сложно, если представлять число в виде дроби 100/4. В этом случае все, что вам нужно сделать, это разделить число на 4 и умножить на 100.

Например, вам нужно умножить 84 на 25. Сначала делим 84 на 4 – получаем 21, а потом умножаем значение выражения на 100. Ответ: 2100.

10. Возведение чисел, оканчивающихся на 5, в квадрат

«Этот математический трюк подразумевает 2 шага», – объясняет Сноу. Чтобы возвести в квадрат число, которое оканчивается на пять, возьмите первую цифру числа и умножьте ее на себя. После этого прибавьте к полученному результату первую цифру и припишите к ответу 25. Кружится голова? Разберем на примере.

Если вы умножаете 35 на 35, сначала умножьте 3 на 3 – получится 9, – и прибавьте 3 к ответу – получится 12. Теперь припишите 25 в конец найденного числа, и вы найдете окончательный ответ: 1225.

11. Вычитание путем сложения

Если вам кажется, что сложение немного проще, чем вычитание, этот трюк для вас. Когда вам нужно найти разность двух чисел, достаточно близких друг к другу, попробуйте решить пример с помощью сложения.

«Вместо того чтобы пытаться вычесть 327 из 334, представьте это в виде суммы: мол, сколько нужно добавить к 327, чтобы получить 334?» – объясняет Сноу.

12. Сложение чисел, оканчивающихся на 99

Если вы пытаетесь прикинуть, во сколько обойдутся продукты, стоимость которых заканчивается на 99, – калькулятор не нужен. Все, что необходимо сделать, – прибавить 100 вместо 99, а потом вычесть единицу.

Сноу объясняет этот процесс на примере 176 + 199 = 375. «Если к 176 мы прибавим 200, то получим 376, – говорит эксперт. – Поскольку вы добавили на единицу больше, чем вам нужно, вычтите ее из 376, чтобы найти правильный ответ: 375».

Источник

Урок 7. Возведение в квадрат в уме

Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.

В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.

Квадрат суммы и квадрат разности

Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:

Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:

Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.

Квадрат близкий к известному квадрату

Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:

На 1 больше:

Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.

На 1 меньше:

Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.

На 2 больше

Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.

На 2 меньше

Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.

Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).

Квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.

Это верно и для более сложных примеров:

Квадрат чисел близких к 50

Считать квадрат чисел, которые находятся в диапазоне от 40 до 60, можно очень простым способом. Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:

Квадрат трехзначных чисел

Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:

Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:

436 2 = (400+30+6) 2 = 400 2 + 30 2 + 6 2 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096

Тренировка

Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.

Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник