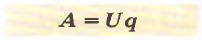как на практике можно определить работу электрического тока в цепи какие для этого нужны приборы

22.07.202202.08.2022 admin 0 Comments

Работа электрического тока: что это такое, формулы, примеры задач

В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.

Что такое работа электрического тока?

Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.

Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.

Определение понятия «электрическая работа» и её единицы измерения.

Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.

Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):

Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.

1 кВт·ч = 1 * 10 3 Вт·ч = 1 * 10 3 * 3600 Вт·с = 3,6 * 10 6 Вт·с = 3,6 * 10 6 Дж.

Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.

По какой формуле вычисляется работа электрического тока?

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.

Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.

Другие формулы для определения работы электрического тока.

Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.

Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:

Примеры задач

У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.

Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:

Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули

27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.

Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:

Источник

§ 50. Работа электрического тока

Как вычислить работу электрического тока? Мы уже знаем, что напряжение на концах участка цепи численно равно работе, которая совершается при прохождении по этому участку электрического заряда в 1 Кл. При прохождезаряда, равного не 1 Кл, а, например, 5 Кл, совершённая работа будет в 5 раз больше. Таким образом, чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи у множить на электрический заряд (количество электричества), прошедший по нему:

где А — работа, U — напряжение, q — электрический заряд. Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения:

Используя это соотношение, получим формулу работы электрического тока, которой удобно пользоваться при расчётах:

Работу измеряют в джоулях, напряжение — в вольтах, силу тока — в амперах и время — в секундах, поэтому можно написать:

1 джоуль = 1 вольт х 1 ампер х 1 секунду,
или 1 Дж = 1 В • А • с.

Выходит, что для измерения работы электрического тока нужны три прибора: вольтметр, амперметр и часы. На практике работу электрического тока измеряют специальными приборами — счётчиками. В устройстве счётчика как бы сочетаются три названных выше прибора. Счётчики электроэнергии сейчас можно видеть почти в каждой квартире.

Запишем условие задачи и решим её.

Вопросы

1. Чему равно электрическое напряжение на участке цепи?
2. Как через напряжение и электрический заряд, прошедший через участок цепи, выразить работу электрического тока на этом участке?
3. Как выразить работу тока через напряжение, силу тока и время?
4. Какими приборами измеряют работу электрического тока?

Упражнение 34

1. Какую работу совершает электрический ток в электродвигателе за 30 мин, если сила тока в цепи 0,5 А, а напряжение на клеммах двигателя 12 В?

2. Напряжение на спирали лампочки от карманного фонаря равно 3,5 В, сопротивление спирали 14 Ом. Какую работу совершает ток в лампочке за 5 мин?

3. Два проводника, сопротивлением по 5 Ом каждый, соединены сначала последовательно, а потом параллельно и в обоих случаях включены под напряжение 4,5 В. В каком случае работа тока за одно и то же время будет больше и во сколько раз?

Источник

Работа и мощность электрического тока. Закон Джоуля-Ленца

1. Электрический ток, проходя по цепи, производит разные действия: тепловое, механическое, химическое, магнитное. При этом электрическое поле совершает работу, и электрическая энергия превращается в другие виды энергии: во внутреннюю, механическую, энергию магнитного поля и пр.

Как было показано, напряжение \( (U) \) на участке цепи равно отношению работы \( (F) \) , совершаемой при перемещении электрического заряда \( (q) \) на этом участке, к заряду: \( U=A/q \) . Отсюда \( A=qU \) . Поскольку заряд равен произведению силы тока \( (I) \) и времени \( (t) \) \( q=It \) , то \( A=IUt \) , т.е. работа электрического тока на участке цепи равна произведению напряжения на этом участке, силы тока и времени, в течение которого совершается работа.

Единицей работы является джоуль (1 Дж). Эту единицу можно выразить через электрические единицы:

\( [A] \) = 1 Дж = 1 В · 1 А · 1 с

Для измерения работы используют три измерительных прибора: амперметр, вольтметр и часы, однако, в реальной жизни для измерения работы электрического тока используют счётчики электрической энергии.

Если нужно найти работу тока, но при этом сила тока или напряжение неизвестны, то можно воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: \( A=\fract \) или \( A=I^2Rt \) .

2. Мощность электрического тока равна отношению работы ко времени, за которое она совершена: \( P=A/t \) или \( P=IUt/t \) ; \( P=IU \) , т.е. мощность электрического тока равна произведению напряжения и силы тока в цепи.

Единицей мощности является ватт (1 Вт): \( [P]=[I]\cdot[U] \) ; \( [P] \) = 1 А · 1 В = 1 Вт.

Используя закон Ома, можно получить другие формулы для расчета мощности тока: \( P=\frac;P=I^2R \) .

Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра, измерив соответственно силу тока и напряжение. Можно для измерения мощности использовать специальный прибор, называемый ваттметром, в котором объединены амперметр и вольтметр.

3. При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: \( Q=A \) или \( Q=IUt \) . Учитывая, что \( U=IR \) , \( Q=I^2Rt \) .

Количество теплоты, выделяющееся при прохождении тока но проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени.

Этот закон называют законом Джоуля-Ленца.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

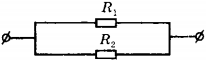
3. Сопротивления резистор \( R_1 \) в четыре раза меньше сопротивления резистора \( R_2 \) . Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1

4. Сопротивление резистора \( R_1 \) в 3 раза больше сопротивления резистора \( R_2 \) . Количество теплоты, которое выделится в резисторе 1

1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2

5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если

1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую

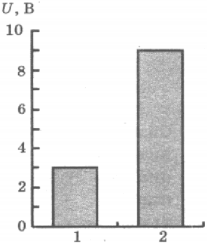
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

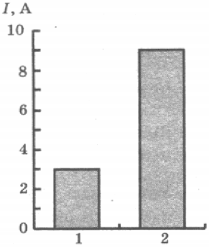
7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то

А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.

Верным(-и) является(-ются) утверждение(-я)

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?

1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А

10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?

1) 10000 с
2) 2000 с
3) 10 с
4) 2 с

11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока

Часть 2

13. Нагреватель включён последовательно с реостатом сопротивлением 7,5 Ом в сеть с напряжением 220 В. Каково сопротивление нагревателя, если мощность электрического тока в реостате составляет 480 Вт?

Источник

§ 50. Работа электрического тока

Как вычислить работу электрического тока? Мы уже знаем, что напряжение на концах участка цепи численно равно работе, которая совершается при прохождении по этому участку электрического заряда в 1 Кл. При прохождении по этому же участку электрического заряда, равного не 1 Кл, а, например, 5 Кл, совершённая работа будет в 5 раз больше. Таким образом, чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (количество электричества), прошедший по нему:

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Работу измеряют в джоулях, напряжение — в вольтах, силу тока — в амперах и время — в секундах, поэтому можно написать:

1 джоуль = 1 вольт х 1 ампер х 1 секунду,

Выходит, что для измерения работы электрического тока нужны три прибора: вольтметр, амперметр и часы. На практике работу электрического тока измеряют специальными приборами — счётчиками. В устройстве счётчика как бы сочетаются три названных выше прибора. Счётчики электроэнергии сейчас можно видеть почти в каждой квартире.

Источник