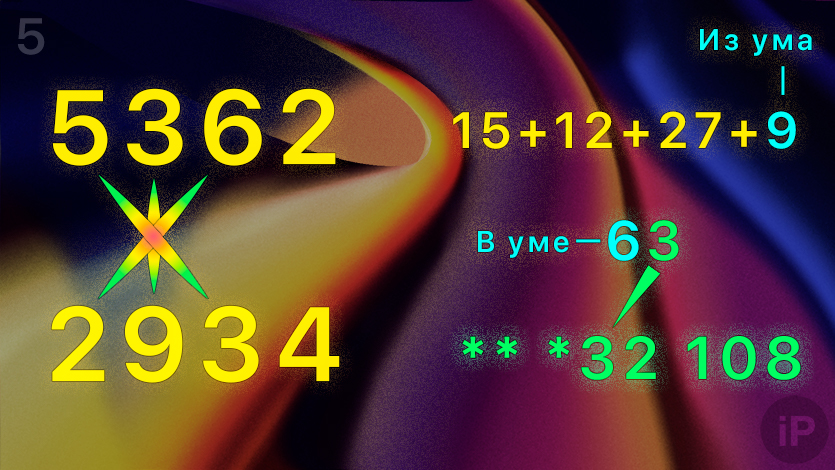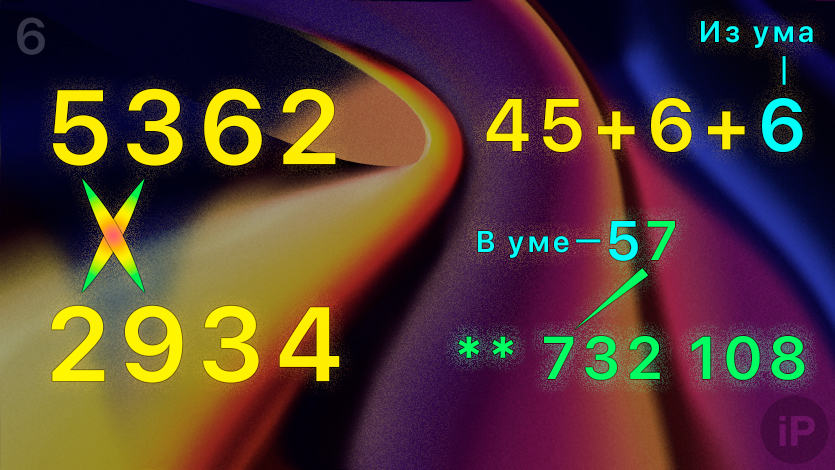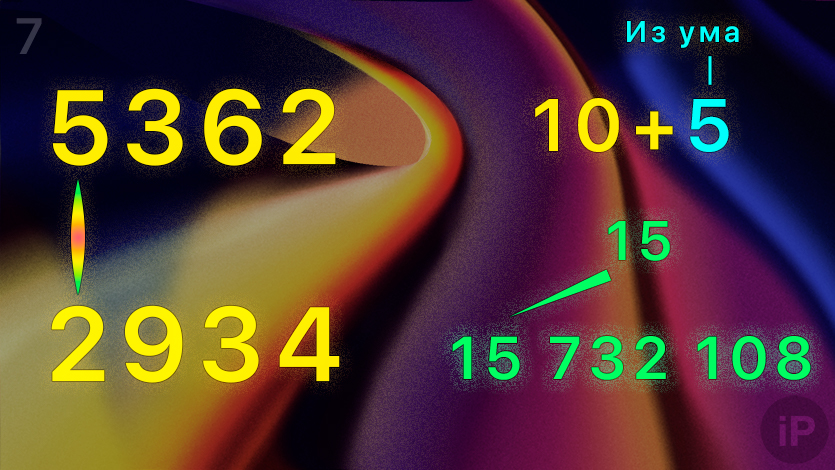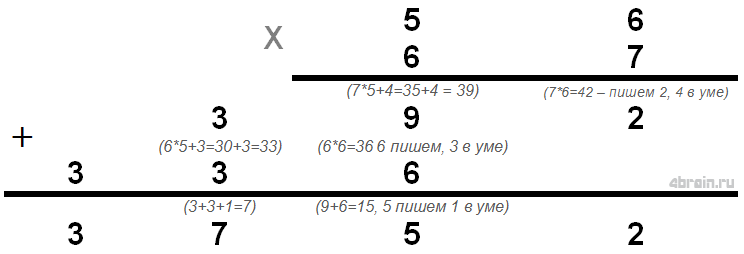как научиться умножать в уме большие числа
Как научиться быстро считать в уме?
Всего несколько месяцев ежедневных тренировок по 5-10 минут, и вы почувствуете, как ускорился ваш мозг.
Сложение
Начнём с простого — сложения однозначных чисел. Научившись мгновенно складывать однозначные числа, вы сможете легко складывать и многозначные числа, потому что все расчёты сводятся к выполнению типовых действий. Вы в этом скоро убедитесь.
Сложение однозначных чисел
С примерами, результаты которых находятся в пределах 10 проблем нет. Эти комбинации чисел нужно просто запомнить, как основу основ.
А вот для примеров «с переходом через 10» уже есть методика — «опора на десяток». Суть в том, чтобы довести одно слагаемое до 10, а потом из второго слагаемого вычесть столько же, сколько мы прибавили к первому.
Например, нам нужно сложить 5 и 8:
Сложение многозначных чисел
Принцип сложения многозначных чисел — складывать друг с другом одинаковые разряды: тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами.
Например, нам нужно сложить 245 и 917:
Вычитание
Как и со сложением, с вычитанием однозначных чисел из однозначных ничего сложного нет. А при вычитании однозначного числа из двузначного удобно пользоваться тем же правилом «опоры на десяток».
Вычитание однозначных числа
Например, нужно вычесть 13 − 7:
Вычитание многозначных чисел
Здесь всё даже проще, чем со сложением многозначных чисел, потому что на разрядные части нужно разложить только то число, которое вычитаем.
Например, нужно вычесть 734 − 427:
Убираем 4 из 314 и 7, получаем 310 − 3. Ну а тут уже совсем просто — ответ 307.
Чтобы вычитать 7, 8 и 9 было проще, часто прибегают к следующим правилам:
321 − 7 = 321 − 10 + 3 = 314
Умножение
Это когда несколько раз складывают одно и то же. Например, 7 × 3 = 7 + 7 + 7 = 21.
Чтобы научиться быстро умножать любые числа в уме (кроме совсем уж космических), нужно идеально умножать однозначные числа, то есть знать таблицу умножения.
Причём идеально знать её необязательно, достаточно запомнить для себя опорные числа, которые будут помогать в вычислениях. Умножим 6 × 7. Мнемотехнически мы знаем что 6 × 6 = 36. То есть к 36 нужно прибавить ещё 6, чтобы получился ответ — 42.
Считается, что из всех примеров в таблице умножения 7 × 8 самый сложный. Чтобы запомнить ответ есть отличное правило «пять шесть семь восемь»: 56 = 7 × 8.
Умножение однозначного числа на двузначное
3 × 8 × 100 = 24 × 100 = 2400.
2400 + 640 + 56 = 2000 + 400 + 600 + 40 + 50 + 6 = 2000 + (400 + 600) + (40 + 50) + 6 = 2000 + 1000 + 90 + 6 = 3000 + 90 + 6 = 3096
Например, 237 × 2. Сначала проще умножить 240 × 2 = 480. А потом вычесть из результата 6 (3 × 2 = 6 — ведь 3 нам не хватало до 240). Итого:
Правда, если сумма двух цифр исходного числа больше 10, нужно поставить разряд единиц между цифрами исходного числа, а десяток прибавить к левой цифре:
Умножение двузначных чисел
Хотя кажется, что умножать двузначные числа — вершина ментальных вычислений, решать такие примеры не сильно сложнее, чем в предыдущем пункте. Давайте разберём на примере.
2490 + 332 = 2000 + 400 + 300 + 90 + 30 + 2 = 2000 + 700 + 120 + 2 = 2822.
Деление
Это операция, обратная умножению. Начнём снова с самого простого.
Деление двузначного числа на однозначное
Разделим 48 : 3. Основная задача — подобрать число, которое можно умножить на 3 и получить 48. Из таблицы умножения мы помним, что единственное число, результат умножения которого на 3 в конце имеет цифру 8 — это 6. А 3 × 6 = 18. То есть, у нас остаётся 30 : 3 = 10. Итого, получается 48 : 3 = 16.
Деление многозначного числа на однозначное
Разделим 6475 : 7. В подобных примерах главная задача — «взять» максимальные «круглые» части, которые можно разделить на 6 без остатка.
Деление на двузначное число
С делением на двузначное число всё гораздо интереснее. Задача в том, чтобы найти пределы, в которых лежит результат.
Например, разделим 6351 : 73:
12 × 25 = 12 : 4 × 100 = 3 × 100 = 300
Этих способов достаточно, чтобы тренироваться уверенно считать в уме. Помните, что делать это нужно регулярно, уделяя всего по 5–10 минут каждый день. Постарайтесь поймать свой ритм, чтобы решение таких задачек приносило удовольствие. И упирайте на правильность ответов, а не скорость — она придёт со временем. И не бросайте.
А если вам нужна помощь в решении более сложных задач, которые уже нельзя просчитать в уме, вам с радостью помогут специалисты Мультиворка.
Без калькулятора: умножаем большие числа в уме
В эру цифровых технологий у нас пропала необходимость запоминать телефоны и адреса, считать в голове. Даже ориентироваться на местности нам помогают гаджеты. Устный счет последний раз мы применяем в школе, а зря. Помимо удобства (ведь вы можете сами быстро все посчитать, не доставая смартфон), умение быстро умножать и делить здорово тренирует мозг. А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.
Гаусс — не только распределение
Еще когда будущий «король математиков» и автор закона, названного его именем, Карл Фридрих Гаусс отличался уникальными навыками. По легенде, примерно в возрасте 3 лет он заметил, что платежные ведомости его отца рассчитаны неправильно. После проверки оказалось, что мальчик был прав. В дальнейшем он продемонстрировал феноменальные математические способности. И некоторые лайфхаки устного счета называют тоже его именем.
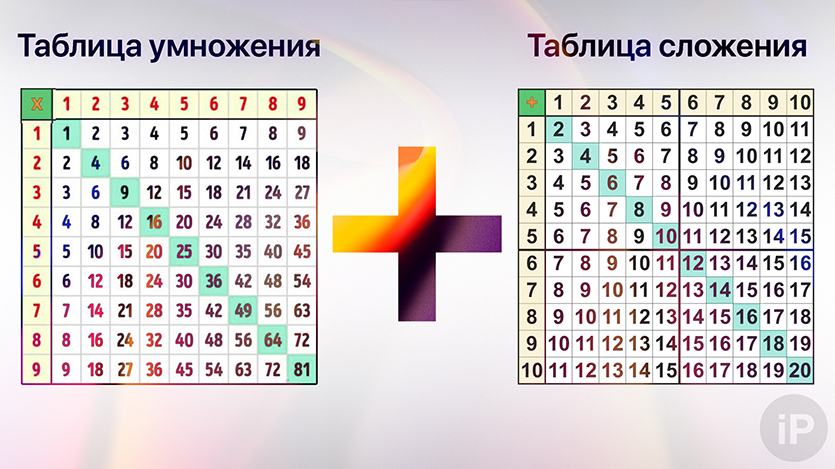
Достаточно одной таблицы
Чтобы научиться перемножать любые числа, нам необходимо помнить таблицу умножения. Хитрость заключается в том, что любое большое число можно разложить на маленькие — те, что представлены в этой таблице. Суть умножения двух чисел заключается в многократном повторении одного из них. Например, 7 умножить на 3 — означает, что число 7 надо повторить 3 раза: 7+7+7 = 7*3 = 21.
Если перед нами стоит задача умножить однозначное число на многозначное, то достаточно разложить больше на маленькие по разрядам, т.е. сначала сотни, потом десятки, потом единицы. И по очереди их умножить на заданное число. Далее останется сложить эти произведения. Например, 254*7 = 200*7 + 50*7 + 4*7 = 1400 + 350 + 28 = 1778. Как мы видим, каждый разряд представляет собой однозначное число с определенным количеством нулей. Таким образом, нам нужно лишь помнить таблицу умножения, чтобы легко справиться с этой задачей.
Этот же способ применим для умножения двух двузначных чисел — их нужно так же разбить на однозначные и выполнить операцию последовательно. Допустим, наша задача умножить 67 на 43. 43 — это 40 + 3. А значит, 67 нужно умножить сначала на 40, затем на 3, и сложить эти произведения. Далее раскладываем 67 и производим ту же операцию. Получаем: 67*40 + 67*3 = 60*40 + 7*40 + 60*3 + 7*3 = 2400 + 280 + 180 + 21 = 2881.
Одиннадцать друзей умножения
Самый простой и интересный способ умножения двузначного числа — с использованием числа 11. Нужно всего лишь сложить между собой цифры, из которых состоит двузначное число. А по бокам поставить те же самые исходные 2 числа, которые мы складывали. Что получится, если 35 умножить на 11? Складываем 3 + 5 = 8, а по бокам ставим 3 и 5 — 385. Проверяем на калькуляторе. Но что делать, если сумма двух этих чисел больше 10? Куда что ставить? Нужно сделать все ровно так же, только при помощи наложения. Посмотрим на примере 83*11: 8 + 3 = 11. Посередине у нас стоит 11, справа 3, а к первому месту прибавляется 8, итого: 8 + 1 = 9 — это первое число. Далее у нас стояла единица, последней тройка. Собираем: 913. Проверяем. Вуаля!
Лайфхаки не тренировка
Конечно, само слово «лайфхак» подразумевает, что мы используем определенный прием, чтобы меньше напрягать мозг. При таком счете мозг тоже тренируется — ведь нам надо удерживать всю раскладку в голове, да еще и складывать эти элементы. Чтобы быстро выучить эти методики, а также дополнительно поддерживать функции мозга в тонусе, нам нужны полноценные тренировки. Они позволят освоить еще больше лайфхаков, быстро адаптироваться в незнакомых ситуациях и не теряться при виде больших данных.
Викиум разработал более 75 специальных — когнитивных тренажеров. Они развивают базовые (когнитивные) функции мозга комплексно, по запатентованной технологии. Программа составляет вам персональный план тренировок, следит за прогрессом, постепенно повышает нагрузку. Сами тренажеры выглядят как игровые задания с понятным интерфейсом — на них могут заниматься даже дети от 7 лет. В результате регулярных тренировок существенно увеличивается работоспособность мозга и ваша общая продуктивность. Занимайтесь каждый день всего по 10 минут и будьте в тонусе!
Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?
В школе всё время слышал «где мне пригодится эта математика?».
И сам задавался таким вопросом. А сейчас вот не хватает учебника для «раскачки» извилин. Например, было бы заметно удобнее считать утерянные цены на Apple или выравнивать пиксельную сетку для иллюстраций.
Но не всё потеряно. Умножать числа в любом возрасте считают проверенным способом подточить ум и даже улучшить психическое здоровье.
Ниже расскажу, где оно ещё может пригодиться и что за секретный способ умножения прокачает ваше знание цифр до уровня интуиции.
Крупный счёт прокачает решение бытовых вопросов
Как любому компьютеру нужно расширять оперативную память, так и нашему мозгу нужен отсек для быстрых операций.
Тренировки с умножением укрепят краткосрочную память. Вы перестанете забывать, закрыли ли дверь на ключ, сколько яиц лежало в холодильнике перед походом в магазин и о чём вели речь после того, как отвлеклись.
Не говоря о том, что будете мгновенно считать, во сколько обойдётся вон тот сочный кусок мяса на шашлык или заправка автомобиля, чтобы доехать до соседнего города.
Вам нужна только математика начальной школы
Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:
I. Знать таблицу умножения
II. Складывать числа
Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.
Отточить умножение поможет приложение УмноЖатель
Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.
Быстро складывать получится точно таким же постоянным запоминанием.
Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.
На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.
Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:
В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.
Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.
Операции с умножением тысячей в уме можно разделить на два типа: умножение на однозначные и многозначные числа.
Как умножить тысячи на однозначное число
Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.
Так выглядит алгоритм:
1. Разбиваем большое число на единицы, десятки, сотни и так далее.
3864 = 3000 + 800 + 60 + 4
2. Умножаем каждый кусочек на второе число.
3000∙7 = 21000 | 800∙7 = 5600 | 60∙7 = 420 | 4∙7 = 28
3. Разбиваем результаты на простые группы одного размера.
21000 = 20000+1000 | 5600=5000+600 | 420 = 400+20 | 28 = 20+8
20000 | 1000+5000 | 600+400 | 20+20 | 8
4. Складываем группы с конца.
20000 + 1000+5000 + 600+400 + 20+20 + 8
20000 + 6000 + 1000 + 40 + 8
Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.
Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.
Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.
Как умножить тысячи на многозначное число
Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.
Запомните метод как Принцип снежинки.
В качестве примера решим 5362∙2934. Алгоритм такой:
0. Представьте числа привычным столбиком.
1. Перемножьте конечные (2∙4) цифры сверху и снизу.
Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.
2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).
Сложите результаты с тем, что храните в уме (24+6+0=30).
Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.
3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).
Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).
Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.
4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).
Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).
Сложите четыре числа и пятое из ума (20+4+9+54+5=92).
Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.
5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).
Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).
Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.
6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).
Сложите результаты с остатком в уме (45+6+6=57).
Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.
7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).
Сложите результат с остатком в уме (10+5=15).
Запишите всё число перед итоговым: 15 732 108.
Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.
Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.
Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.
Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.
Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.
И тогда сможете считать миллионы, не коснувшись бумаги.
Урок 3. Традиционное умножение в уме

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Искусство умножения двузначных чисел в уме
Люди всегда стремились найти лучшие способы выполнения вычислений. Чем стремительнее развивается прогресс, тем более актуальными становятся высокие математические способности. Даже тот человек, карьера которого не предполагает работу с цифрами, ежедневно вынужден прибегать к счету в уме. Походы за покупками, оплата коммунальных счетов, планирование семейного бюджета – все это требует большого количество подсчетов. Конечно, можно полагаться на технику, ведь в каждом современном смартфоне присутствует калькулятор. Но все же стоит помнить, что умение быстро считать – это возможность существенно оптимизировать свои собственные ресурсы, поэтому развивать такие навыки важно.
Умножение в уме
В современном мире цифры окружают нас везде. Ежедневно мы не задумываясь выполняем десятки и даже сотни простых арифметических действий, но, стоит только столкнуться с более сложными числовыми операциями, и большинство людей машинально потянется к калькулятору. Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.
Складывать и вычитать устно – этому человек учится еще в школе. Со временем, удается научиться без труда производить вычисления даже с большими значениями. Конечно, это утверждение справедливо только для простых операций, таких как сложение и вычитание, а вот умножение освоить уже не так легко. В школе от детей требуется научиться умножать только на множитель от одного до десяти, а более сложные подсчеты допустимо производить на бумаге. Таким образом, ученикам не прививается умение выполнять умножение больших чисел в уме, этим навыкам можно обучиться только дополнительно.
Умение быстро считать очень полезно, так как оно используется ежедневно. Поэтому сегодня придумано множество подходов к счету. Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.
Популярные методы устного умножения
Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:
Вариант 1. Умножение в столбик
Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.
Сначала необходимо умножить 34 на единицы второго числа: 34*3=102. Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142
Вариант 2. Умножение с разложением на десятки и единицы
Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.
Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.
Вариант 3. Умножение с большими числами
Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.
Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.
Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.
Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.
Быстрое умножение в уме больших чисел
Математики всех времен искали простые методы быстрого устного счета. Умножение и деление, в отличие от сложения и вычитания, являются более сложными операциями. Поэтому производить такие подсчеты в уме без должной подготовки сложно, тем более когда речь идет о многозначных числах. Проблема устного умножения в том, что не существует какого-либо универсального способа, который бы подходил вне зависимости от ситуации.
Мозг обычного человека не способен работать также быстро, как калькулятор. Мы склонны терять концентрацию, сбиваться, забывать результаты промежуточных операций. Поэтому стандартные способы устного умножения мало пригодны для повседневных задач. Они скорее являются хорошей разминкой для мозга, чем удобным инструментом. Но что делать, если быстро считать без подручных средств все же хочется?
Благодаря интернету можно найти немало информации по этому вопросу. Сегодня существует множество методик, позволяющих научиться складывать, вычитать, умножать и даже делить с моментальной скоростью. Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.
Лучший способ научиться устному счету
Ментальная арифметика – это не только уникальный способ счета без подручных средств. В основе этой методики лежит равнозначное развитие как левого полушария мозга, отвечающего за логику и анализ, так и правого, которое контролирует работу воображения и фантазии. Несмотря на то, что освоить ментальную арифметику может любой желающий, она все же больше подходит для изучения в раннем возрасте. Именно в детстве можно приобрести навыки, которые не забудутся со временем и сохранятся на всю жизнь.
Обучение ментальной арифметике – длительный процесс, который требует усидчивости и нацеленности на результат. Пройдет немало времени, пока ребенок сможет полностью освоить программу и научиться не только складывать и вычитать, но и умножать и делить многозначные числа. Родителям не всегда удается контролировать периодичность занятий своего ребенка, а также следить за тем, чтобы он выполнял все необходимые упражнения. Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.
Ученики, обучающиеся по этому направлению, сначала осваивают вычисления на древних счетах – абакусе. Когда базовые навыки закрепятся, наступает время для перехода к следующему, более сложному этапу. Теперь ученик постепенно привыкает представлять абакус в своем воображении и производить подсчеты уже на нем. Именно так и удается развить навык быстрого счета.
Благодаря занятиям ментальной арифметикой ребенок повышает успеваемость в школе, ведь теперь ему доступны не только простые вычисления в уме, но и быстрое умножение и деление. Количество времени, которое он тратит на выполнение домашних заданий, также сокращается. Так удается добиться большей продуктивности образовательного процесса в школе и дома. Навыки, приобретенные благодаря ментальной арифметике, сохранятся навсегда, что очень пригодится во взрослой жизни.