как запоминать числа в уме
Эффективный счёт в уме или разминка для мозга
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
Теперь не кажется невозможным умножить в уме 625 на 53:
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
Тогда предыдущий пример можно вычислить немного проще:
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Оптимальный способ запоминания цифр
Итак, начнем.
Освещу популярные способы запоминания цифр:
Способ 1: Использование звуковой памяти:
1) Подбирается фраза, в которой число букв в каждом слове соответствует очередной цифре числа:
«Это я знаю и помню прекрасно,
Пи многие знаки мне лишни, напрасны»
Соответственно расшифровывается как 3,14159265358
2) Или в которой рифмуются сами цифры:
«Чтобы ПИ запомнить, братцы,
Надо чаще повторять:
Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять»
Преимущество: легко подбирать слова и составлять из них предложения, а так же расшифровывать.
Недостаток: при запоминании длинных цифровых комбинаций
(например: 7-мизначный номер телефона) придется составлять длинные предложения. Даже при небольшом количестве длинных предложений можно запутаться, не говоря уже о большом.
Способ 2: Использование образной памяти
1) Одна цифра:
Единица — кол, деревяшка в ошмётках коры, шершавая на ощупь. Двойка — лебедь, белоснежный и толстый и так далее для всех цифр.
2)Две и более:
После создания образного ряда запоминание цифр превращается в игру, похожую на рисование мультфильма.
Например, для запоминания числа 21 можно представить себе лебедя, на которого упал кол, ушиб его и лебедь злобно шипит и щиплет кол. Таким образом, вместо абстрактных цифр в памяти появляются движущиеся картинки, которые легко и прочно в ней удерживаются.
Преимущество: фантазия человека всегда найдет образное сравнение для любой комбинации цифр.
Недостаток: тот же, что и в способе 1: при запоминании, к примеру, телефона получается длинный «мультик», а если телефонов несколько, то картинки из «мультиков» могут перепутаться между собой.
Способ 3: Использование раскладки телефонной клавиатуры
Цифры заменяются соответствующими буквами из телефонной клавиатуры, а из букв составляются слова. Например: Телефонный номер Яндекса: 8-800-333-96-39, для запоминания предложен текстовый вариант номера: 8-800-333-YNDX
Преимущество: цифровой ряд запоминается легче, если заменить сложные для восприятия его части буквами, образующими некую фразу, либо слово.
Недостаток: цифры 0 и 1 не имеют буквенных значений в телефонной клавиатуре, поэтому запоминать их с помощью этого способа не получится, что является большим недостатком, так как это 1/5 всех существующих цифр (речь идет о 10-тичной системе счисления, в которой считает большинство людей).
Способ 4: Цифро-буквенный алфавит
Суть его заключается в том, что каждой цифре ставятся в соответствие какие-то буквы, а из букв составляются слова. Алфавитов таких известно несколько.
Вот один из них:
0. Буквы Н и Л в слове «НоЛь».
1. Р от слова «Раз».
2. Д — «Два» и Г, так как эта цифра больше всего напоминает данную маленькую букву.
3. Т от «Три» и 3 — по внешнему сходству.
4. Ч от слова «Четыре» (и, кстати, напоминает внешним видом), но более часто К от слова «Квадрат».
5. П — «Пять» и Б, по схожести звучания (и по внешнему виду).
6. Ш — «Шесть» и Ж, тоже по схожести звучания.
7. С — «Семь», и, обычно этого хватает, так как С — очень распространённая буква.
8. В — «Восемь» (внешнее сходство тоже сильное) и, иногда, сходное по звучанию Ф.
9. Здесь сложнее. Можно М от слова «Много», так как 9 самая большая цифра.
Например, число 3312 можно записать как «тетрадь».
Преимущество: малый размер получающихся фраз, так как в одном слове может быть закодировано несколько цифр. Легкость расшифровки (зависит от кодировки: есть интуитивно-понятные, а есть те, что нужно заучивать как таблицу умножения).
Недостаток: необходимо подбирать слова по получившимся буквам и предложения по словам, а это, иногда, бывает затруднительным. А так же запоминать «кодировку» — соответствие цифрам определенных букв.
Подведем мини-итог:
Наиболее эффективный способ – цифро-буквенный алфавит, потому что при его использовании получаются компактные фразы, что уменьшает риск перепутать слова из разных фраз. Так же достигается большая вариативность фраз, благодаря богатому русскому языку (в словаре Даля зафиксировано более 200’000 словарных единиц).
Начнем творчество
Стоит создать свою цифро-буквенную кодировку, понятную большинству людей и в то же время, что немаловажно, эффективную. В русском языке насчитывается 20 подходящих согласных. Гласные не используется, поскольку тогда почти не будет подходящих слов. 20 согласных. 10 цифр.
Пусть будет 2 колонки букв, подходящих цифрам. Первая — интуитивно понятная, вторая будет компенсировать первую в плане эффективности.
0. Н от слова «Ноль»
1. Р от слова «Раз»
2. Д — «Два»
3. Т — «Три»
4. Ч — «Четыре
5. П — «Пять»
6. Ш — «Шесть»
7. С — «Семь»
8. В — «Восемь»
9. З – так как буква Д уже занята, используем З, похожую на 9 внешне
Эти буквы интуитивно-понятны.
Почему именно так? Как была создана эта колонка?
Так вот, каждой букве первой колонки подбиралась пара так, что бы среднее арифметическое от суммы частотности их использования в русском языке примерно равнялось остальным средним арифметическим. Это повысит вариативность возможных слов.
Назовем ее ОЦБК – Оптимальная Цифро-Буквенная Кодировка.
Теперь, к примеру, можно преобразовать число 412 в слово «очередь», 86-79 в «ваш союз» или «воля семьи» и так далее. Также возможно и обратное преобразование: «желтый картон» выглядит как 763-41-30, «поле для ввода» – 562-68-82.
Актуальность и сферы применения
В настоящее время люди стали слишком зависимы от электроники, интернета. Решение данной проблемы поможет снизить нашу зависимость от электронных устройств, ведь нам уже не придется записывать номера телефонов, даты и прочее в запоминающие электронные устройства. Так же это повысит эффективность обучения. К примеру: школьникам не придется зубрить даты, числа и т.п.
Данную методику можно применять в повседневной жизни – запоминать номера телефонов, кредитных карт, Яндекс-денег…В обучении, для запоминания дат, констант и другой цифровой информации. При этом отпадает необходимость иметь с собой записанные данные, снижается риск их утери, что в свою очередь снижает риск использования ваших данных злоумышленниками.
Программа
Так же написал программу, которая сама подбирает слова по заданным цифрам и преобразует цифры в слова. В программе будут подбираться слова по заданным цифрам. Цифры, разделенные ‘-‘ считаются отдельными. Например: 1234 и 12-34, это не одно и то же. В первом случае будет произведен поиск по комбинации «1234», во втором — по двум комбинациям «12» и «34».
Как запоминать большие числа? “Накрутка” интеллекта)))
Большинство людей не могут запомнить за 30 секунд число длиннее, чем 7 цифр. А если надо запомнить 20-значное число, то тут у всех возникают большие сложности. Многие не помнят 10-значный номер своего мобильного телефона. А если кто-то и знает, то чаще всего на это потребовалось какое-то время и усилия.
Оказывается, запоминать длинные числа не так уж и сложно, если вы выучили главную систему запоминания. При помощи этой системы вы каждому числу сопоставляете зрительный образ, и запоминать в итоге вам надо не цифры, а слова. Если вы освоили главную систему от 0 до 100, то тогда, если вам надо запомнить 10-значный номер телефона, вам надо всего лишь запомнить 5 слов.
Например, пусть вам надо запомнить телефон 965 462 73 28. Разобьем номер на двузначные числа и сопоставим им слова-образы в соответствии с главной системой:
Теперь вам вместо 10 цифр надо запомнить 5 слов. А это уже намного легче. 5 слов можно легко запомнить и без мнемотехник. Но если использовать принципы отличной памяти и мнемотехники для запоминания списков, то тогда 5 слов можно запомнить практически мгновенно.
Если вы освоите главную систему от 0 до 10 000, то тогда задача запомнить 100-значное число сводится к запоминанию двадцати пяти слов (100-значное число – это всего лишь 25 четырехзначных чисел). А двадцать пять слов при помощи системы римской комнаты любой сможет запомнить за 1-2 минуты. Система римской комнаты заключается в том, что вы раскладываете все предметы на заранее продуманные места в хорошо знакомой вам комнате или квартире. Но если предметов очень много, то вы просто захламите комнату и запутаетесь. Поэтому гораздо лучше работает, если вы расставляете все предметы по порядку вдоль хорошо знакомой улицы или в космосе, например, рядом или вместо звезд и планет.
Соломон Шерешевский и Доминик О’Брайн, известные своей феноменальной памятью, делали именно так! Каждому числу у них соответствовал какой-то образ – предмет или человек, а чтобы запомнить длинный ряд чисел, они расставляли эти предметы вдоль знакомой длинной улицы.
Однако можете использовать для запоминания больших чисел любой из способов запоминания длинных списков предметов, описанных в статье “Как быстро запоминать длинные списки покупок, слов и дел“.
Меня поразило, как легко и быстро можно запоминать длинные числа. И это доступно любому из нас! А ведь в некоторых тестах на оценку интеллекта необходимо запоминать большие числа. Освоив эти несложные техники, вы сможете легко “накрутить” свой коэффициент интеллекта))).
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет
Карл Фридрих Гаусс
Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Таблица умножения
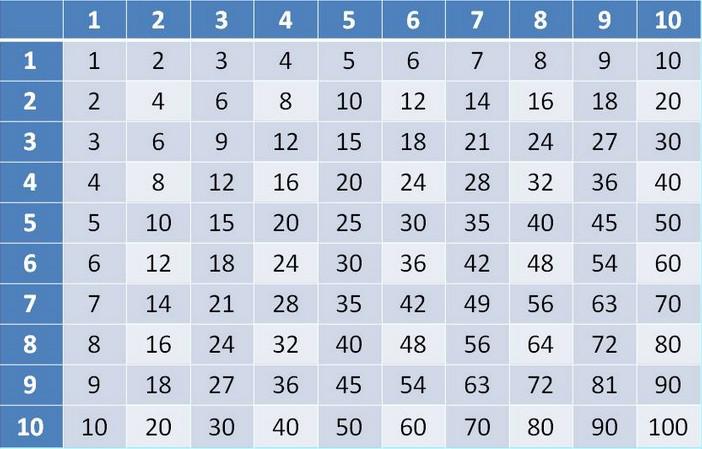
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.
Раньше все считали без калькуляторов
Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.
Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»
Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.