классические методы машинного обучения
Machine Learning – не только нейронки
Нейронные сети и глубокое обучение (deep learning) у всех на слуху, но нейросети – это лишь подобласть такого обширного предмета, как машинное обучение (machine learning). Существует несколько сотен других алгоритмов, которые способны быстро и эффективно решать задачи искусственного интеллекта и в большинстве случаев являются более интерпретируемыми для человека. В этой статье рассмотрим алгоритмы классического машинного обучения, принцип работы нейросетей, подготовку данных для обучения моделей и задачи, которые решают с помощью искусственного интеллекта.
Основные задачи машинного обучения
Восстановление регрессии (прогнозирования) – построение модели, способной предсказывать численную величину на основе набора признаков объекта.
Классификация – определение категории объекта на основе его признаков.
Кластеризация – распределение объектов.
Допустим, есть набор данных со статистикой по приложениям. В нем есть следующие сведения: размер, категория, количество скачиваний, количество отзывов, рейтинг, возрастной рейтинг, жанр и цена. С помощью этого набора данных и машинного обучения можно решить такие задачи:
Прогнозирование рейтинга приложения на основе признаков: размер, категория, возрастной рейтинг, жанр и цена – задача регрессии.
Определение категории приложения на основе набора признаков: размер, возрастной рейтинг, жанр и цена – задача классификации.
Разбиение приложений на группы на основании множества признаков (например, количество отзывов, скачиваний, рейтинга) таким образом, чтобы приложения внутри группы были более похожи друг на друга, чем приложения разных групп.
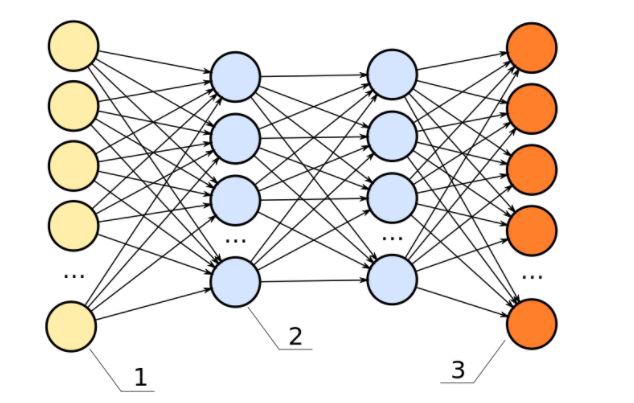
Нейронные сети (многослойный перцептрон)
Существует мнение, что лучшие идеи для изобретений человек заимствует у природы. Нейронные сети – это именно тот случай, ведь сама концепция нейросетей базируется на функциональных особенностях головного мозга.
Принцип работы
Есть определенное количество нейронов, которые между собой связаны и взаимодействуют друг с другом путем передачи сигналов. Также есть рецепторы, которые получают информацию, поступающую извне, и исполнительный орган, на который приходит итоговый сигнал. По схожему принципу работают искусственные нейросети: есть несколько слоев с нейронами и связи между ними (каждая связь имеет свой весовой коэффициент). По связям передаются сигналы в виде численных значений, первый слой выполняет собой роль рецепторов, то есть получает набор признаков для обучения, и есть выходной слой, который выдает ответ.


Каждый слой нейросети оперирует разными представлениями о данных. На рисунке ниже можно увидеть пример использованиям глубокого обучения (нейросети) для распознавания образа на картинке. На входной слой нам поступают пиксели изображений, далее после вычислений между входным и первым скрытым слоем мы получаем границы, на втором скрытом слое – контуры, на третьем – части объектов, на выходном – вероятности принадлежности изображения к каждому типу объектов.

Как настраивать
Настраивается путем задания количества узлов, скрытых слоев и выбора функции активации. В искусственных нейронных сетях функция активации нейрона отвечает за выходной сигнал, который определяется входным сигналом или набором входных сигналов.
Задачи: классификация, регрессия, кластеризация.
Классические алгоритмы машинного обучения
K-ближайших соседей
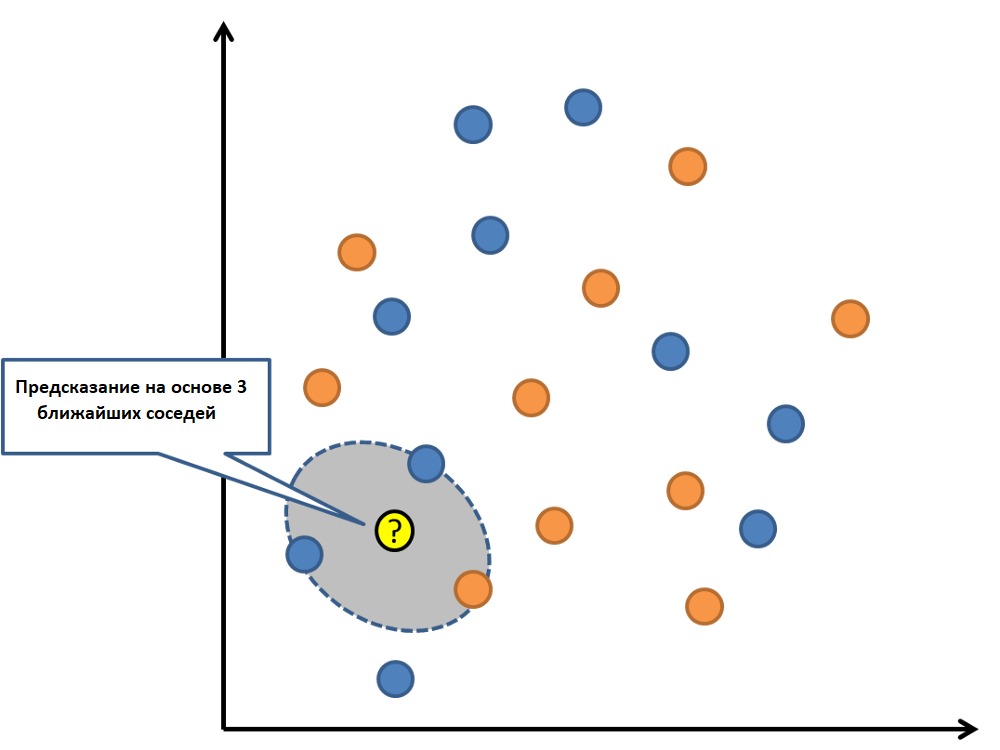
Метод K-ближайших соседей – простой и эффективный алгоритм, его можно описать известной поговоркой: “Скажи мне, кто твой друг, и я скажу, кто ты”.
Принцип работы
Пусть имеется набор данных с заданными классами. Мы можем определить класс неизвестного объекта, если рассмотрим определенное количество ближайших объектов (k) и присвоим тот класс, который имеет большинство “соседей”. Посмотрим на рисунок ниже.
Есть набор точек с двумя классами: синие крестики и красные кружки. Мы хотим определить, к какому классу относится неизвестная зеленая точка. Для этого мы берем k ближайших соседей, в данном случае 3, и смотрим, к каким классам они относятся. Из трех ближайших соседей больше оказалось синих крестиков, соответственно, мы можем предположить, что зеленая точка также, скорее всего, относится к этому классу.
Как настраивать
Необходимо подобрать параметр k (количество ближайших соседей) и метрику для измерения расстояний между объектами.
Задачи: классификация, также может применяться и для задач регрессии.
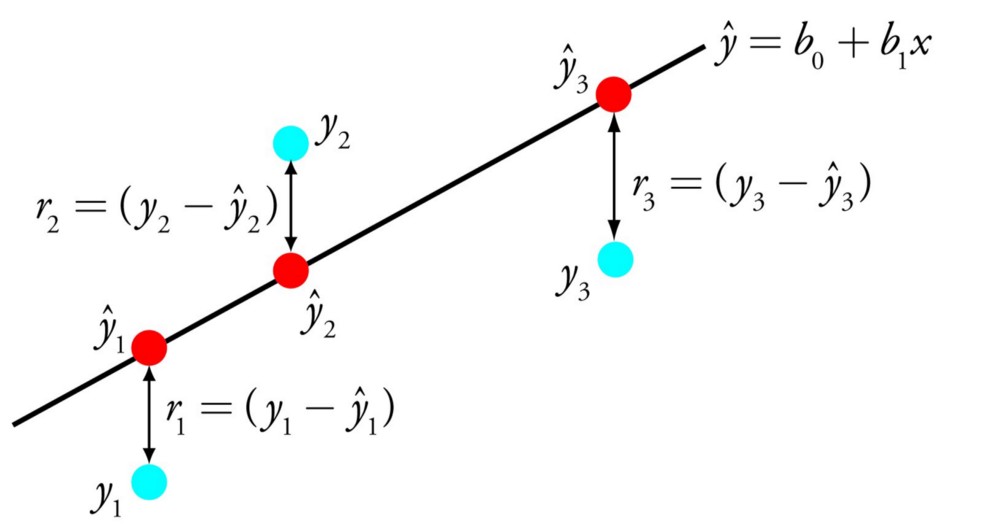
Линейная регрессия
Линейная регрессия – простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.
Принцип работы
Модель линейной регрессии можно описать уравнением
Здесь x – это значения признаков, y – целевая переменная, a – весовые коэффициенты признаков. При обучении модели весовые коэффициенты подбираются таким образом, чтобы как можно лучше описывалась линейная зависимость признаков от целевой переменной.
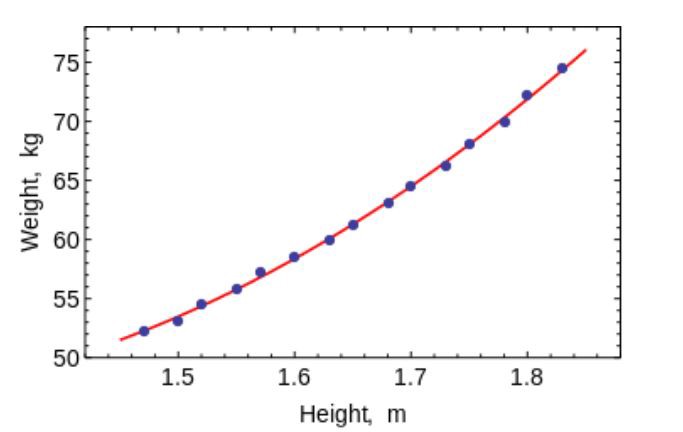
Пример: задача предсказания стоимости квартиры в зависимости от площади и удаленности от метро в минутах. Целевой переменной (y) будет являться стоимость, а признаками (x) – площадь и удаленность.
На рисунке ниже также представлен пример построения линейной регрессии. Красная прямая более точно описывает линейную зависимость x от y.
Как настраивать
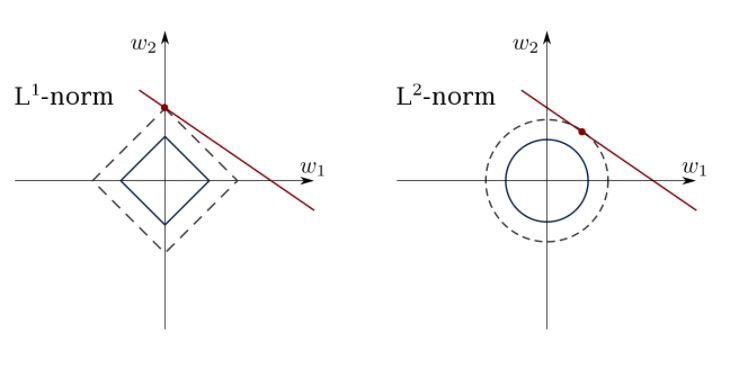
Для многих моделей Machine Learning, в частности и для линейной регрессии, можно улучшить итоговое качество с помощью регуляризации.
Регуляризация в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение, то есть ситуацию, когда модель хорошо показывает себя на тренировочный данных, но перестаёт работать на новых.
Распространенные методы регуляризации для повышения качества модели линейной регрессии:
Ridge — один из методов понижения размерности. Применяется для борьбы с переизбыточностью данных, когда независимые переменные коррелируют друг с другом (мультиколлинеарность), вследствие чего проявляется неустойчивость оценок коэффициентов линейной регрессии.
LASSO — также как и Ridge, применяется для борьбы с переизбыточностью данных.
Elastic-Net — модель регрессии с двумя регуляризаторами L1, L2. Частными случаями являются модели LASSO L1 = 0 и Ridge регрессии L2 = 0.
Задачи: регрессия.
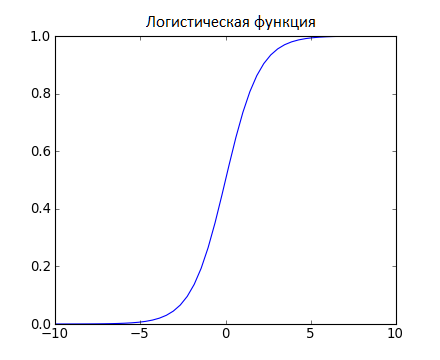
Логистическая регрессия
Логистическая регрессия – также простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.
Принцип работы
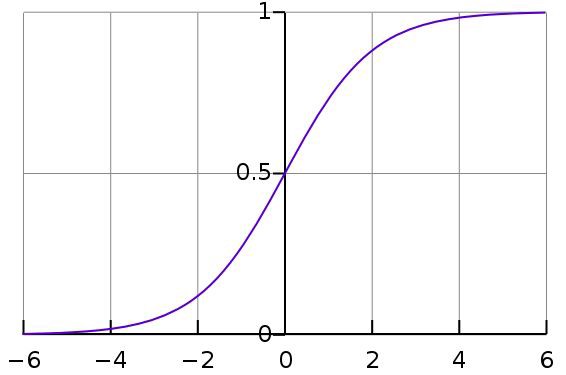
Указанная выше сумма проходит через функцию сигмоиды, которая возвращает число от 0 до 1, характеризующее вероятность отнесения объекта к классу 1. Пример: логистическую регрессию часто применяют в задачах кредитного скоринга, когда по определенным данным о клиенте нужно определить, стоит ли выдавать ему кредит.
Иллюстрация алгоритмов линейной и логистической регрессии (источник)
Как настраивать
Задачи: классификация.
Метод опорных векторов (SVM)
Принцип работы
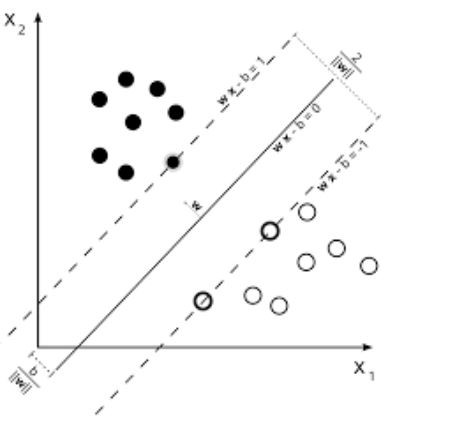
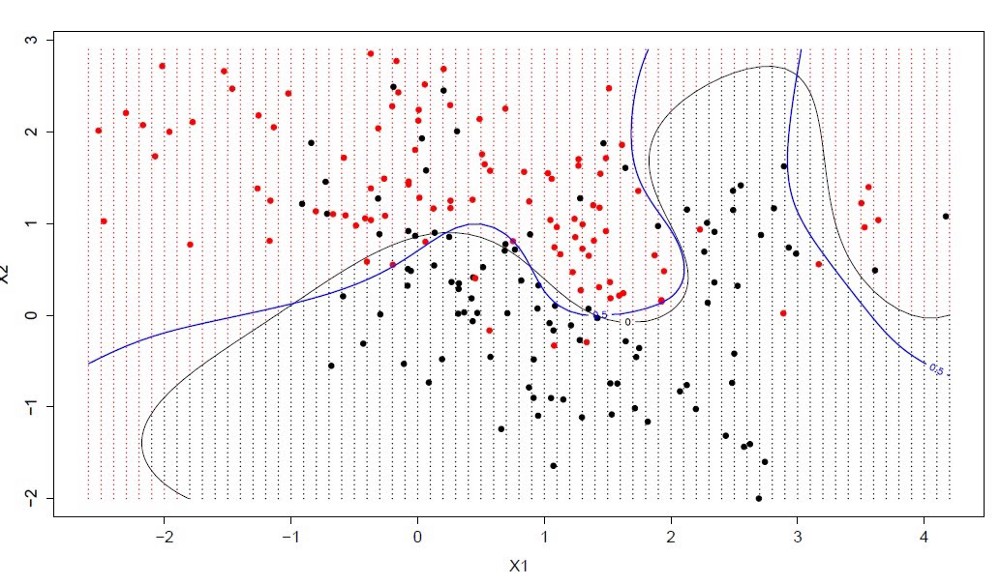
Чтобы лучше всего понять алгоритм метода опорных векторов, рассмотрим рисунок. На рисунке приведен пример двух линейно разделимых классов в двумерном пространстве. Идея алгоритма заключается в нахождении оптимальной разделяющей прямой (или гиперплоскости для более высоких пространств) для отделения объектов одного класса от другого. Пунктирные линии выделяют разделяющую полосу и проводятся через объекты, которые называют опорными. Чем шире разделяющая полоса, тем качественнее модель SVM. Чтобы определить класс объекта, достаточно определить, с какой стороны гиперплоскости он находится.
Как настраивать
Необходимо подобрать оптимальное ядро (функцию переводящую признаковое пространство в более высокую размерность), если линейная зависимость слабо выражена.
Задачи: классификация и регрессия.
Сравнение классических алгоритмов с нейросетью
Для примера мы взяли датасет со статистикой приложений в Play Market. Датасет содержит следующие данные: размер приложения, возрастной рейтинг, количество скачиваний, жанр, категория и др. На данном датасете были обучены модели: линейная регрессия, метод опорных векторов, нейронная сеть (многослойный перцептрон).
В ходе экспериментов были подобраны следующие параметры для моделей машинного обучения:
Линейная регрессия – модели линейной регрессии с регуляризацией не показали результат, превосходящий качество классической линейной регрессии.
Метод опорных векторов – модель метода опорных векторов с RBF-ядром показала лучший результат по сравнению с другими ядрами.
Многослойный перцептрон – оптимальный результат показала модель с 4 слоями, 300 нейронами и функций активацией ReLu. При попытках увеличить количество слоев и нейронов прирост качества не наблюдался.
Решена задача прогнозирования потенциального рейтинга приложения в зависимости от его признаков.
Результаты ошибки среднего отклонения от истинного значения целевой переменной в процентах для каждой модели:
Линейная регрессия – 6.13 %
Метод опорных векторов – 6.01%
Нейронная сеть – 6.41%
Таким образом, классические алгоритмы машинного обучения и нейросети показали приблизительно одинаковое качество. Это связано с тем, что нейросети хорошо обучаются на датасетах с большим размером и обычно применяются для решения задач, где зависимость в данных очень сложна. Поэтому для решения данной задачи можно обойтись применением классических алгоритмов и не прибегать к использованию нейросетей.
На гистограмме ниже представлены итоговые весовые коэффициенты a, полученные при обучении модели линейной регрессии. Чем больше столбик, тем выше влияние признака на целевую переменную. Если столбик направлен вверх, то он оказывает положительное влияние на рост целевой переменной, если вниз – то отрицательное. Другими словами, если приложение имеет жанр “Other” или “Tools”, то, скорее всего, его рейтинг будет высоким, а если у него категория “FAMILY” или “GAME” – то, вероятно, низким. Данная интерпретация весовых коэффициентов линейной регрессии бывает очень полезной при анализе данных.

Больше наших статей по машинному обучению и обработке изображений:
Must-have алгоритмы машинного обучения
Этот пост — краткий обзор общих алгоритмов машинного обучения. К каждому прилагается краткое описание, гайды и полезные ссылки.
Метод главных компонент (PCA)/SVD
Это один из основных алгоритмов машинного обучения. Позволяет уменьшить размерность данных, потеряв наименьшее количество информации. Применяется во многих областях, таких как распознавание объектов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных.
SVD — это способ вычисления упорядоченных компонентов.
Метод наименьших квадратов
Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, а также для аппроксимации точечных значений некоторой функции.
Используйте этот алгоритм, чтобы соответствовать простым кривым/регрессии.
Ограниченная линейная регрессия
Метод наименьших квадратов может смутить выбросами, ложными полями и т. д. Нужны ограничения, чтобы уменьшить дисперсию линии, которую мы помещаем в набор данных. Правильное решение состоит в том, чтобы соответствовать модели линейной регрессии, которая гарантирует, что веса не будут вести себя “плохо”. Модели могут иметь норму L1 (LASSO) или L2 (Ridge Regression) или обе (elastic regression).
Используйте этот алгоритм для соответствия линиям регрессии с ограничениями, избегая переопределения.
Метод k-средних
Всеми любимый неконтролируемый алгоритм кластеризации. Учитывая набор данных в виде векторов, мы можем создавать кластеры точек на основе расстояний между ними. Это один из алгоритмов машинного обучения, который последовательно перемещает центры кластеров, а затем группирует точки с каждым центром кластера. Входные данные – количество кластеров, которые должны быть созданы, и количество итераций.
Логистическая регрессия
Логистическая регрессия ограничена линейной регрессией с нелинейностью (в основном используется сигмоидальная функция или tanh) после применения весов, следовательно, ограничение выходов приближено к + / — классам (что равно 1 и 0 в случае сигмоида). Функции кросс-энтропийной потери оптимизированы с использованием метода градиентного спуска.
Примечание для начинающих: логистическая регрессия используется для классификации, а не регрессии. В целом, она схожа с однослойной нейронной сетью. Обучается с использованием методов оптимизации, таких как градиентный спуск или L-BFGS. NLP-разработчики часто используют её, называя “классификацией методом максимальной энтропии”.
Используйте LR для обучения простых, но очень “крепких” классификаторов.
SVM (Метод опорных векторов)
SVM – линейная модель, такая как линейная/логистическая регрессия. Разница в том, что она имеет margin-based функцию потерь. Вы можете оптимизировать функцию потерь, используя методы оптимизации, например, L-BFGS или SGD.
Одна уникальная вещь, которую могут выполнять SVM – это изучение классификаторов классов.
SVM может использоваться для обучения классификаторов (даже регрессоров).
Нейронные сети прямого распространения
В основном, это многоуровневые классификаторы логистической регрессии. Многие слои весов разделены нелинейностями (sigmoid, tanh, relu + softmax и cool new selu). Также они называются многослойными перцептронами. FFNN могут быть использованы для классификации и “обучения без учителя” в качестве автоэнкодеров.
FFNN можно использовать для обучения классификатора или извлечения функций в качестве автоэнкодеров.
Свёрточные нейронные сети
Практически все современные достижения в области машинного обучения были достигнуты с помощью свёрточных нейронных сетей. Они используются для классификации изображений, обнаружения объектов или даже сегментации изображений. Изобретенные Яном Лекуном в начале 90-х годов, сети имеют сверточные слои, которые действуют как иерархические экстракторы объектов. Вы можете использовать их для работы с текстом (и даже для работы с графикой).
Рекуррентные нейронные сети (RNNs)
RNNs моделируют последовательности, применяя один и тот же набор весов рекурсивно к состоянию агрегатора в момент времени t и вход в момент времени t. Чистые RNN редко используются сейчас, но его аналоги, например, LSTM и GRU являются самыми современными в большинстве задач моделирования последовательности. LSTM, который используется вместо простого плотного слоя в чистой RNN.
Используйте RNN для любой задачи классификации текста, машинного перевода, моделирования языка.
Условные случайные поля (CRFs)
Они используются для моделирования последовательности, как RNN, и могут использоваться в сочетании с RNN. Они также могут быть использованы в других задачах структурированных прогнозирования, например, в сегментации изображения. CRF моделирует каждый элемент последовательности (допустим, предложение), таким образом, что соседи влияют на метку компонента в последовательности, а не на все метки, независимые друг от друга.
Используйте CRF для связки последовательностей (в тексте, изображении, временном ряду, ДНК и т. д.).
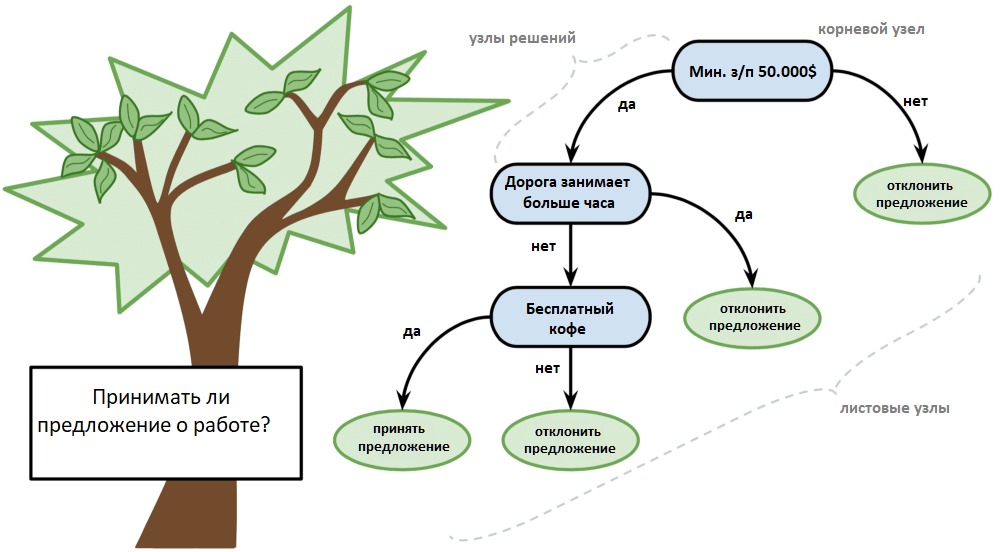
Деревья принятия решений и случайные леса
Один из самых распространённых алгоритмов машинного обучения. Используется в статистике и анализе данных для прогнозных моделей. Структура представляет собой “листья” и “ветки”. На “ветках” дерева решения записаны атрибуты, от которых зависит целевая функция, в “листьях” записаны значения целевой функции, а в остальных узлах – атрибуты, по которым различаются случаи.
Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких входных переменных.
Обзор самых популярных алгоритмов машинного обучения
Авторизуйтесь
Обзор самых популярных алгоритмов машинного обучения
Существует такое понятие, как «No Free Lunch» теорема. Её суть заключается в том, что нет такого алгоритма, который был бы лучшим выбором для каждой задачи, что в особенности касается обучения с учителем.
Например, нельзя сказать, что нейронные сети всегда работают лучше, чем деревья решений, и наоборот. На эффективность алгоритмов влияет множество факторов вроде размера и структуры набора данных.
По этой причине приходится пробовать много разных алгоритмов, проверяя эффективность каждого на тестовом наборе данных, и затем выбирать лучший вариант. Само собой, нужно выбирать среди алгоритмов, соответствующих вашей задаче. Если проводить аналогию, то при уборке дома вы, скорее всего, будете использовать пылесос, метлу или швабру, но никак не лопату.
18–20 ноября, Онлайн, Беcплатно
Представляем вашему вниманию краткий обзор топ-10 популярных алгоритмов, используемых в машинном обучении.
1. Линейная регрессия
Линейная регрессия — пожалуй, один из наиболее известных и понятных алгоритмов в статистике и машинном обучении.
Прогностическое моделирование в первую очередь касается минимизации ошибки модели или, другими словами, как можно более точного прогнозирования. Мы будем заимствовать алгоритмы из разных областей, включая статистику, и использовать их в этих целях.
Например: Y = B0 + B1 * X
Для оценки регрессионной модели используются различные методы вроде линейной алгебры или метода наименьших квадратов.
Линейная регрессия существует уже более 200 лет, и за это время её успели тщательно изучить. Так что вот пара практических правил: уберите похожие (коррелирующие) переменные и избавьтесь от шума в данных, если это возможно. Линейная регрессия — быстрый и простой алгоритм, который хорошо подходит в качестве первого алгоритма для изучения.
Логистическая регрессия — ещё один алгоритм, пришедший в машинное обучение прямиком из статистики. Её хорошо использовать для задач бинарной классификации (это задачи, в которых на выходе мы получаем один из двух классов).
Логистическая регрессия похожа на линейную тем, что в ней тоже требуется найти значения коэффициентов для входных переменных. Разница заключается в том, что выходное значение преобразуется с помощью нелинейной или логистической функции.
Логистическая функция выглядит как большая буква S и преобразовывает любое значение в число в пределах от 0 до 1. Это весьма полезно, так как мы можем применить правило к выходу логистической функции для привязки к 0 и 1 (например, если результат функции меньше 0.5, то на выходе получаем 1) и предсказания класса.
Благодаря тому, как обучается модель, предсказания логистической регрессии можно использовать для отображения вероятности принадлежности образца к классу 0 или 1. Это полезно в тех случаях, когда нужно иметь больше обоснований для прогнозирования.
Как и в случае с линейной регрессией, логистическая регрессия выполняет свою задачу лучше, если убрать лишние и похожие переменные. Модель логистической регрессии быстро обучается и хорошо подходит для задач бинарной классификации.
3. Линейный дискриминантный анализ (LDA)
Логистическая регрессия используется, когда нужно отнести образец к одному из двух классов. Если классов больше, чем два, то лучше использовать алгоритм LDA (Linear discriminant analysis).
Представление LDA довольно простое. Оно состоит из статистических свойств данных, рассчитанных для каждого класса. Для каждой входной переменной это включает:
Предсказания производятся путём вычисления дискриминантного значения для каждого класса и выбора класса с наибольшим значением. Предполагается, что данные имеют нормальное распределение, поэтому перед началом работы рекомендуется удалить из данных аномальные значения. Это простой и эффективный алгоритм для задач классификации.
4. Деревья принятия решений
Дерево решений можно представить в виде двоичного дерева, знакомого многим по алгоритмам и структурам данных. Каждый узел представляет собой входную переменную и точку разделения для этой переменной (при условии, что переменная — число).
Листовые узлы — это выходная переменная, которая используется для предсказания. Предсказания производятся путём прохода по дереву к листовому узлу и вывода значения класса на этом узле.
Деревья быстро обучаются и делают предсказания. Кроме того, они точны для широкого круга задач и не требуют особой подготовки данных.
Наивный Байес — простой, но удивительно эффективный алгоритм.
Модель состоит из двух типов вероятностей, которые рассчитываются с помощью тренировочных данных:
После расчёта вероятностной модели её можно использовать для предсказания с новыми данными при помощи теоремы Байеса. Если у вас вещественные данные, то, предполагая нормальное распределение, рассчитать эти вероятности не составляет особой сложности.
Наивный Байес называется наивным, потому что алгоритм предполагает, что каждая входная переменная независимая. Это сильное предположение, которое не соответствует реальным данным. Тем не менее данный алгоритм весьма эффективен для целого ряда сложных задач вроде классификации спама или распознавания рукописных цифр.
6. K-ближайших соседей (KNN)
К-ближайших соседей — очень простой и очень эффективный алгоритм. Модель KNN (K-nearest neighbors) представлена всем набором тренировочных данных. Довольно просто, не так ли?
Предсказание для новой точки делается путём поиска K ближайших соседей в наборе данных и суммирования выходной переменной для этих K экземпляров.
Вопрос лишь в том, как определить сходство между экземплярами данных. Если все признаки имеют один и тот же масштаб (например, сантиметры), то самый простой способ заключается в использовании евклидова расстояния — числа, которое можно рассчитать на основе различий с каждой входной переменной.
KNN может потребовать много памяти для хранения всех данных, но зато быстро сделает предсказание. Также обучающие данные можно обновлять, чтобы предсказания оставались точными с течением времени.
Идея ближайших соседей может плохо работать с многомерными данными (множество входных переменных), что негативно скажется на эффективности алгоритма при решении задачи. Это называется проклятием размерности. Иными словами, стоит использовать лишь наиболее важные для предсказания переменные.
Недостаток KNN заключается в том, что нужно хранить весь тренировочный набор данных. Если KNN хорошо себя показал, то есть смысл попробовать алгоритм LVQ (Learning vector quantization), который лишён этого недостатка.
LVQ представляет собой набор кодовых векторов. Они выбираются в начале случайным образом и в течение определённого количества итераций адаптируются так, чтобы наилучшим образом обобщить весь набор данных. После обучения эти вектора могут использоваться для предсказания так же, как это делается в KNN. Алгоритм ищет ближайшего соседа (наиболее подходящий кодовый вектор) путём вычисления расстояния между каждым кодовым вектором и новым экземпляром данных. Затем для наиболее подходящего вектора в качестве предсказания возвращается класс (или число в случае регрессии). Лучшего результата можно достичь, если все данные будут находиться в одном диапазоне, например от 0 до 1.
8. Метод опорных векторов (SVM)
Метод опорных векторов, вероятно, один из наиболее популярных и обсуждаемых алгоритмов машинного обучения.
Гиперплоскость — это линия, разделяющая пространство входных переменных. В методе опорных векторов гиперплоскость выбирается так, чтобы наилучшим образом разделять точки в плоскости входных переменных по их классу: 0 или 1. В двумерной плоскости это можно представить как линию, которая полностью разделяет точки всех классов. Во время обучения алгоритм ищет коэффициенты, которые помогают лучше разделять классы гиперплоскостью.
Расстояние между гиперплоскостью и ближайшими точками данных называется разницей. Лучшая или оптимальная гиперплоскость, разделяющая два класса, — это линия с наибольшей разницей. Только эти точки имеют значение при определении гиперплоскости и при построении классификатора. Эти точки называются опорными векторами. Для определения значений коэффициентов, максимизирующих разницу, используются специальные алгоритмы оптимизации.
Метод опорных векторов, наверное, один из самых эффективных классических классификаторов, на который определённо стоит обратить внимание.
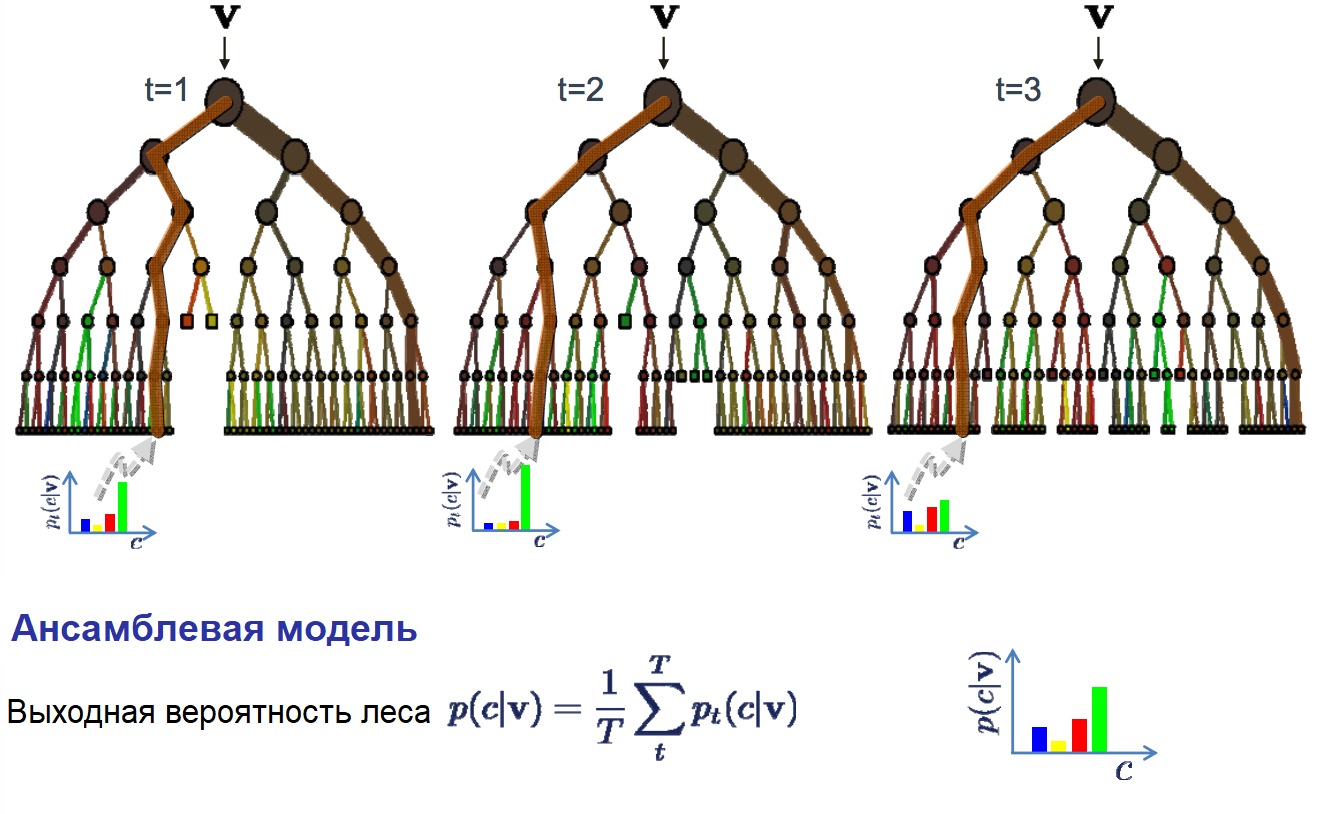
Случайный лес — очень популярный и эффективный алгоритм машинного обучения. Это разновидность ансамблевого алгоритма, называемого бэггингом.
Бутстрэп является эффективным статистическим методом для оценки какой-либо величины вроде среднего значения. Вы берёте множество подвыборок из ваших данных, считаете среднее значение для каждой, а затем усредняете результаты для получения лучшей оценки действительного среднего значения.
В бэггинге используется тот же подход, но для оценки всех статистических моделей чаще всего используются деревья решений. Тренировочные данные разбиваются на множество выборок, для каждой из которой создаётся модель. Когда нужно сделать предсказание, то его делает каждая модель, а затем предсказания усредняются, чтобы дать лучшую оценку выходному значению.
В алгоритме случайного леса для всех выборок из тренировочных данных строятся деревья решений. При построении деревьев для создания каждого узла выбираются случайные признаки. В отдельности полученные модели не очень точны, но при их объединении качество предсказания значительно улучшается.
Если алгоритм с высокой дисперсией, например, деревья решений, показывает хороший результат на ваших данных, то этот результат зачастую можно улучшить, применив бэггинг.
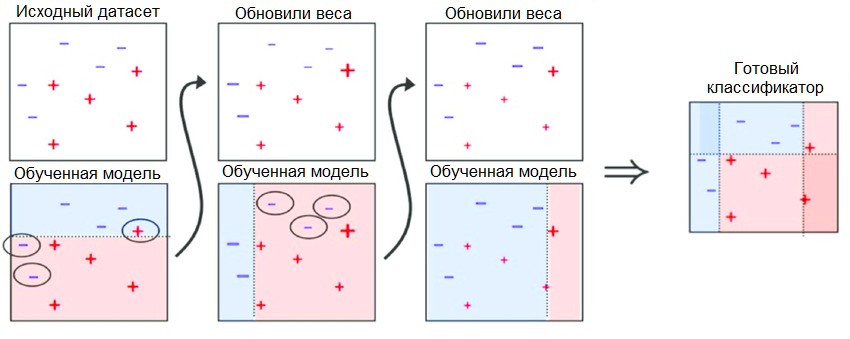
Бустинг — это семейство ансамблевых алгоритмов, суть которых заключается в создании сильного классификатора на основе нескольких слабых. Для этого сначала создаётся одна модель, затем другая модель, которая пытается исправить ошибки в первой. Модели добавляются до тех пор, пока тренировочные данные не будут идеально предсказываться или пока не будет превышено максимальное количество моделей.
AdaBoost был первым действительно успешным алгоритмом бустинга, разработанным для бинарной классификации. Именно с него лучше всего начинать знакомство с бустингом. Современные методы вроде стохастического градиентного бустинга основываются на AdaBoost.
AdaBoost используют вместе с короткими деревьями решений. После создания первого дерева проверяется его эффективность на каждом тренировочном объекте, чтобы понять, сколько внимания должно уделить следующее дерево всем объектам. Тем данным, которые сложно предсказать, даётся больший вес, а тем, которые легко предсказать, — меньший. Модели создаются последовательно одна за другой, и каждая из них обновляет веса для следующего дерева. После построения всех деревьев делаются предсказания для новых данных, и эффективность каждого дерева определяется тем, насколько точным оно было на тренировочных данных.
Так как в этом алгоритме большое внимание уделяется исправлению ошибок моделей, важно, чтобы в данных отсутствовали аномалии.
Пара слов напоследок
Когда новички видят всё разнообразие алгоритмов, они задаются стандартным вопросом: «А какой следует использовать мне?» Ответ на этот вопрос зависит от множества факторов:
Даже опытный data scientist не скажет, какой алгоритм будет работать лучше, прежде чем попробует несколько вариантов. Существует множество других алгоритмов машинного обучения, но приведённые выше — наиболее популярные. Если вы только знакомитесь с машинным обучением, то они будут хорошей отправной точкой.