кодирование числовой информации представление числовой информации
Кодирование числовой информации представление числовой информации
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятк ов, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления
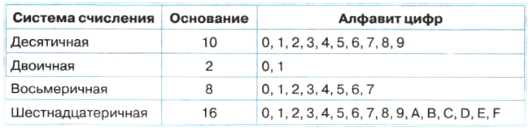
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Урок 18
Кодирование числовой информации. Системы счисления
§ 4.1. Кодирование числовой информации
Содержание урока
4.1.1. Представление числовой информации с помощью систем счисления
4.1.1. Представление числовой информации с помощью систем счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из знаков, которые называются цифрами.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью знаков некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу (рис. 4.1). Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме.
Рис. 4.1. Единичная система счисления
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М (рис. 4.2).
Рис. 4.2. Римская система счисления
В римской системе счисления значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятерок, единиц. Например, десятичное число 28 представляется следующим образом:
10 + 10 + 5 + 1 + 1 + 1 = XXVIII
(два десятка, пятерка, три единицы).
При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный справа от большего, прибавляется к большему знаку, а каждый меньший знак, поставленный слева от большего, вычитается из большего знака.
Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Например, число 99 имеет следующее представление в римской системе счисления:
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения цифр в соседних разрядах числа различаются в количество раз, равное основанию системы.
В настоящее время наиболее распространенной позиционной системой счисления является десятичная система. В информатике широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления.
Десятичная система счисления (табл. 4.1). В десятичной системе счисления цифра в крайней справа позиции обозначает количество единиц, цифра, смещенная на одну позицию влево, обозначает количество десятков, еще левее — сотен, затем тысяч и т. д. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на число 10 в различных степенях, где 10 является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записано следующим образом:
Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:
Двоичная система счисления (см. табл. 4.1). Числа в двоичной системе в развернутой форме записываются в виде суммы основания 2 в различных степенях с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево. Например:
Восьмеричная система счисления (см. табл. 4.1). В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр <0, 1, 2, 3, 4, 5, 6, 7>. Запишем восьмеричное число в свернутой и развернутой формах:
Шестнадцатеричная система счисления (см. табл. 4.1). В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр <0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F>, причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр со значениями 10, 11, 12, 13, 14, 15 используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой формах:
Таблица 4.1. Позиционные системы счисления
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т. е. в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т. д.
Контрольные вопросы
1. Чем отличаются позиционные системы счисления от непозиционных?
2. Каково основание десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
3. Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
4. Во сколько раз в позиционных системах счисления различаются значения цифр соседних разрядов числа?
5. Может ли в качестве цифры в системе счисления использоваться символ буквы?
Задания для самостоятельного выполнения
4.1. Задание с кратким ответом. Запишите числа 3,1410 и 10,12 в развернутой форме.
4.2. Задание с кратким ответом. Во сколько раз увеличатся числа 10,110 и 10,12 при переносе запятой на один знак вправо?
4.3. Задание с кратким ответом. При переносе запятой на два знака вправо число 11,11х увеличилось в 4 раза. Чему равно основание х системы счисления?
4.4. Задание с кратким ответом. Какое минимальное основание может иметь система счисления, если в ней записано число 11? Число 99?
4.5. Задание с кратким ответом. Запишите год, месяц и число своего рождения с помощью римских цифр.
Cкачать материалы урока
Кодирование числовой информации
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Кодирование числовой информации
Тип урока: комбинированный урок.
Обучающие: Познакомиться с системами счисления.
Развивающие: Иметь представление о способах представления числовых данных.
Воспитательные: Развитие познавательного интереса, логического мышления.
Оборудование: демонстрационный экран, компьютер, карточки с заданием.
1. Организационный этап.
Подготовка учащихся к работе на уроке.
2. Подготовка учащихся к сознательному усвоению нового материала.
Учитель: Сегодня мы с вами познакомимся с основными принципами записи числовой информации, узнаем о новом понятии – системе счисления и рассмотрим, какие системы счисления бывают. Тема сегодняшнего урока: “Кодирование числовой информации”.
Приложение 1. Слайд 1. Кодирование числовой информации.
— Что такое информация?
Ученики: Это сведения, получаемые нами из окружающего мира.
Ученики: С помощью органов чувств.
Ученики: Текстовая, символьная, графическая, музыкальная.
3. Усвоение новых знаний.
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами.
Приложение 1. Слайд 2. Определение системы счисления.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Приложение 1. Слайд 3. Позиционные, непозиционные системы счисления.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления.
В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Приложение 1. Слайд 4. Непозиционные системы счисления.
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50, 100, 500 и 1000 используются латинские буквы L, С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе ХХХ (30) цифра Х встречается трижды и в каждом случае обозначает одну и туже величину – число 10, три раза по 10 в сумме дают 30.
Приложение 1. Слайд 5. Пример римской системы счисления.
XХVIII = 10 + 10 + 5 + 1 + 1 + 1.
Приложение 1. Слайд 6. Позиционная система счисления.
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значение одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем тысячи и т. д.
Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Приложение 1.Слайд 7. Таблица – позиционная система счисления.
В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских цифр. Алфавит двоичной системы – две цифры.
| Система счисления | Основание | Алфавит цифр |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 2 | 0, 1 |
Любое число, записанное в позиционной системе счисления с произвольным основанием, можно записать в развернутой форме.
Приложение 1. Слайд 8. Пример записи чисел в развернутой форме.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
55510 = 5*10 2 + 5*10 1 + 5*10°.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:
Число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.
Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
Человек использует десятичную систему счисления, а компьютер – двоичную. Поэтому часто возникает необходимость перевода чисел из десятичной системы счисления в двоичную и наоборот.
Приложение 1. Слайд 9. Перевод чисел из двоичной системы счисления в десятичную.
Преобразование чисел из двоичной системы счисления в десятичную выполнит довольно легко. Для этого необходимо записать двоичное число в развернутой форме и вычислить его значение.
Возьмем двоичное число 10,112. запишем его в развернутой форме и произведем вычисления:
Приложение 1. Слайд 10. Перевод чисел из десятичной системы счисления в двоичную.
Алгоритм перевода десятичного числа в двоичное следующий:
1) последовательно выполнять деление исходного десятичного числа и получаемых частных на основание системы счисления (2) до тех пор, пока частное от деления не окажется равным единице;
2) получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.
Приложение 1. Слайд 11. Перевод чисел из десятичной системы счисления в двоичную.
В качестве примера рассмотрим перевод десятичного числа 1910 в двоичную систему счисления.
4. Закрепление нового материала.
Учитель: А для того, чтобы проверить и закрепить изученный материал, мы выполним тестовую работу (3-5 минут).
1. Верно ли, что число 1001101 может быть записано в двоичной системе счисления?
2. Верно ли, что римская система счисления непозиционная?
3. Верно ли, что в компьютерах используется римская система счисления?
4. Верно ли, что для сложных арифметических вычислений удобно пользоваться римской системой счисления?
5. Верно ли, что в двоичной системе счисления существует цифра 2?
1. Верно ли, что число 23222112 может быть записано в четырехричной системе счисления?
2. Верно ли, что арабские цифры удобны для сложных арифметических вычислений?
3. Верно ли, что в памяти компьютера используется десятичная система счисления?
4. Верно ли, что все системы счисления делятся на две большие группы?
5. Верно ли, что десятичная система счисления позиционная?
Учитель: А сейчас проверим ваши работы. Поменяемся работами с соседом.
| Вариант | Номера ответов | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | да | да | нет | нет | нет |
| 2 | да | да | нет | да | да |
Отработка практических навыков.
1. Решите следующие примеры:
2. Какие числа записаны римскими цифрами:
3. Запишите год, месяц и число своего рождения с помощью римских цифр.
4. Запишите в развернутом виде числа:
5. Запишите в свернутой форме следующие числа:
6. Правильно ли записаны числа в соответствующих системах счисления:
7. Переведите из десятичной системы счисления в двоичную число 5610.
8. Чему равен десятичный эквивалент числа 101012?
5. Подведение итогов урока, домашнее задание.
Сегодня мы с вами познакомились с системами счисления, рассмотрели примеры перевода чисел из десятичной системы счисления в двоичную и обратно.
На следующих уроках мы займемся практической работой по переводу чисел из одной системы счисления в другую и научимся производить арифметические операции с двоичными числами.
Домашнее задание: § 4. 1. 1 и 4. 1. 2. страница 104, контрольные вопросы и задания для самостоятельного выполнения [2].
Кодирование числовой информации
Вы будете перенаправлены на Автор24
Десятичное и двоичное представление чисел
Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.
Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.
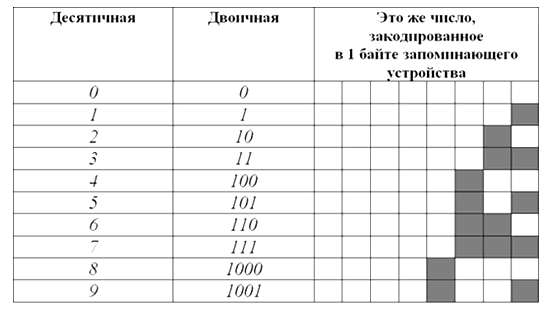
Вот таблица первых десяти чисел в каждой из этих систем счисления:
Готовые работы на аналогичную тему
Алгоритмы кодирования чисел в двоичной системе счисления
Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:
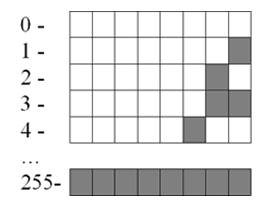
Небольшие целые числа без знака.
Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:
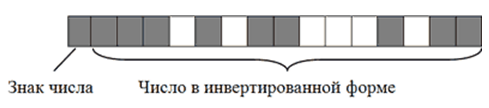
Большие целые числа и числа со знаком.
Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.
Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.
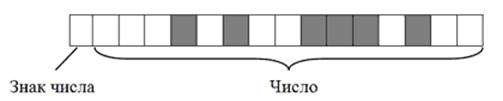
Дробные числа со знаком.
Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.
Порядок кодирования будет примерно следующим:
Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс».
