кодирование числовой информации системы счисления
Презентация была опубликована 9 лет назад пользователемaliya-polovnikova.narod.ru
Похожие презентации
Презентация на тему: » Кодирование числовой информации Системы счисления.» — Транскрипт:
1 Кодирование числовой информации Системы счисления
2 Кодирование информации Кодирование информации – это процесс формирования определенного представления информации, то есть переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Существует 3 способа кодирования текста: Графический Символьный Числовой
3 Система счисления Числа записываются с помощью особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
4 Виды систем счисления Позиционные СС– количественное значение цифры зависит от ее положения в числе Непозиционные СС – количественное значение цифры не зависит от ее положения в числе 0, XIX
5 Непозиционные системы счисления Единичная СС (количество предметов отображали равным количеством зарубок, засечек, черточек, точек и тп.) Римская СС (В качестве цифр используются: I(1), V(5), X(10), L(50), C(100), D(500), M(1000)) При записи чисел в римской СС применяется правило : каждый меньший знак, поставленный слева от большего, вычитается из него, в остальных случаях – знаки складываются MCMXCVIII = 1000+( )+(100-10) = 1998
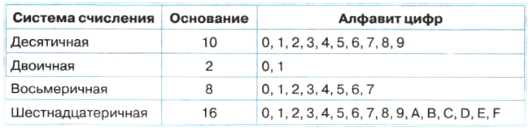
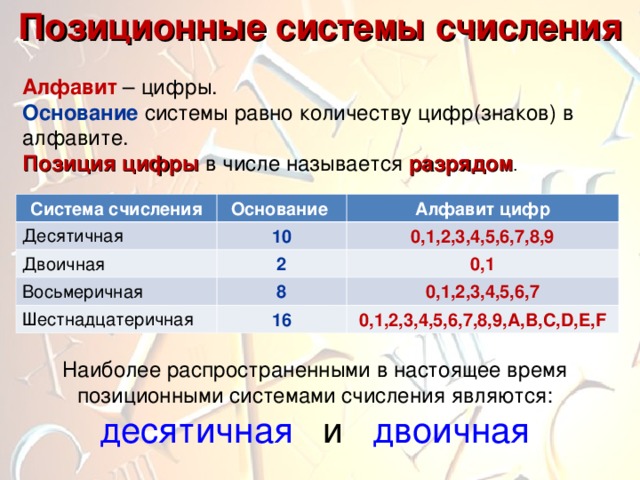
6 Позиционные системы счисления Основание системы равно количеству цифр (знаков) в ее алфавите Система счисления Основание Алфавит цифр Десятичная100, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двоичная20, 1 Восьмеричная80, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная160, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Позиция цифры в числе называется разрядом
Кодирование числовой информации системы счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятк ов, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Урок 18
Кодирование числовой информации. Системы счисления
§ 4.1. Кодирование числовой информации
Содержание урока
4.1.1. Представление числовой информации с помощью систем счисления
4.1.1. Представление числовой информации с помощью систем счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из знаков, которые называются цифрами.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью знаков некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу (рис. 4.1). Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме.
Рис. 4.1. Единичная система счисления
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М (рис. 4.2).
Рис. 4.2. Римская система счисления
В римской системе счисления значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятерок, единиц. Например, десятичное число 28 представляется следующим образом:
10 + 10 + 5 + 1 + 1 + 1 = XXVIII
(два десятка, пятерка, три единицы).
При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный справа от большего, прибавляется к большему знаку, а каждый меньший знак, поставленный слева от большего, вычитается из большего знака.
Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Например, число 99 имеет следующее представление в римской системе счисления:
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения цифр в соседних разрядах числа различаются в количество раз, равное основанию системы.
В настоящее время наиболее распространенной позиционной системой счисления является десятичная система. В информатике широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления.
Десятичная система счисления (табл. 4.1). В десятичной системе счисления цифра в крайней справа позиции обозначает количество единиц, цифра, смещенная на одну позицию влево, обозначает количество десятков, еще левее — сотен, затем тысяч и т. д. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на число 10 в различных степенях, где 10 является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записано следующим образом:
Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:
Двоичная система счисления (см. табл. 4.1). Числа в двоичной системе в развернутой форме записываются в виде суммы основания 2 в различных степенях с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево. Например:
Восьмеричная система счисления (см. табл. 4.1). В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр <0, 1, 2, 3, 4, 5, 6, 7>. Запишем восьмеричное число в свернутой и развернутой формах:
Шестнадцатеричная система счисления (см. табл. 4.1). В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр <0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F>, причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр со значениями 10, 11, 12, 13, 14, 15 используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой формах:
Таблица 4.1. Позиционные системы счисления
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т. е. в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т. д.
Контрольные вопросы
1. Чем отличаются позиционные системы счисления от непозиционных?
2. Каково основание десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
3. Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
4. Во сколько раз в позиционных системах счисления различаются значения цифр соседних разрядов числа?
5. Может ли в качестве цифры в системе счисления использоваться символ буквы?
Задания для самостоятельного выполнения
4.1. Задание с кратким ответом. Запишите числа 3,1410 и 10,12 в развернутой форме.
4.2. Задание с кратким ответом. Во сколько раз увеличатся числа 10,110 и 10,12 при переносе запятой на один знак вправо?
4.3. Задание с кратким ответом. При переносе запятой на два знака вправо число 11,11х увеличилось в 4 раза. Чему равно основание х системы счисления?
4.4. Задание с кратким ответом. Какое минимальное основание может иметь система счисления, если в ней записано число 11? Число 99?
4.5. Задание с кратким ответом. Запишите год, месяц и число своего рождения с помощью римских цифр.
Cкачать материалы урока
Кодирование числовой информации
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Презентация к уроку информатики «Кодирование числовой информации. Системы счисления»
Презентация к уроку информатики «Кодирование числовой информации. Системы счисления». Разработка предназначена для изучения нового материала по теме учащимися 8 класса.
Содержимое разработки
«Кодирование числовой информации. Системы счисления»
Записать в тетрадь
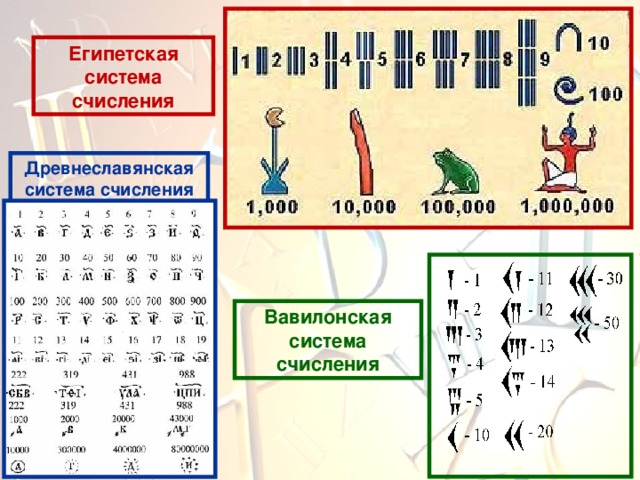
Египетская система счисления
Древнеславянская система счисления
Вавилонская система счисления
Виды систем счисления
(количественное значение цифры не зависит от её положения в числе)
(количественное значение цифры зависит от её положения в числе)
Непозиционные системы счисления
Единичная система счисления
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Римская система счисления
Римская система счисления начала применяться более 2,5 тысяч лет назад в Древнем Риме.
В этой системе отсутствует нуль.
Непозиционная система счисления
Числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению,
а каждый меньший знак, поставленный слева от большего, вычитается из него.
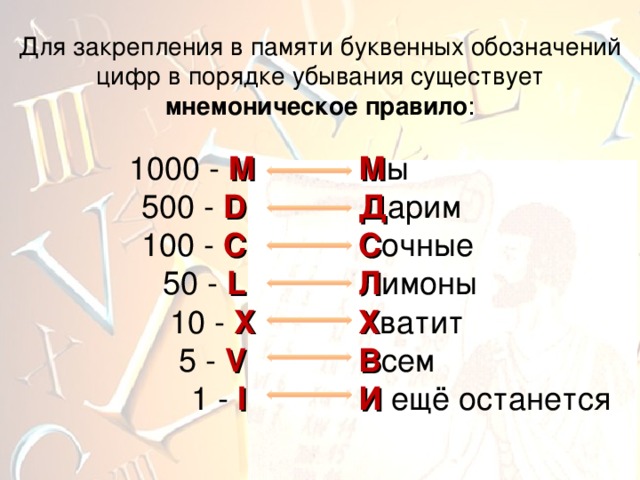
Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило :
Запись римскими цифрами
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Запишем их вместе: M CM LXXX VIII
Запись римскими цифрами
Правильно ли записаны числа? Если нет, укажите правильное написание.
Позиционные системы счисления
Основание системы равно количеству цифр(знаков) в алфавите.
Наиболее распространенными в настоящее время позиционными системами счисления являются:
десятичная и двоичная
Алфавитные системы счисления
Пятеричная система счисления
Десятичная система счисления
Двенадцатеричная система счисления
Двадцатеричная система счисления
Шестидесятеричная система счисления
АЛФАВИТНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Алфавитные системы счисления представляют особую группу. В них для записи чисел использовался буквенный алфавит. Примером алфавитной системы счисления является славянская. У одних славянских народов числовые значения букв устанавливались в порядке следования букв славянского алфавита, у других, в частности у русских, роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите. Над буквой, обозначающей цифру, ставился специальный знак – “титло”. Славянская система счисления сохранилась в богослужебных книгах.
АЛФАВИТНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Алфавитная система счисления была распространена у древних армян, грузин, греков (ионическая система счисления), арабов, евреев, и других народов Ближнего востока.
В древнеармянском и древнегрузинском
алфавитах было гораздо больше букв,
чем в древнегреческом.
Это позволило ввести особые обозначения
1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000 , 9000.
ПЯТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
По свидетельству известного исследователя Африки Стэнли, у ряда африканских племен была распространена пятеричная система счисления.
Долгое время пользовались пятеричной системой счисления и в Китае.
Очевидна связь этой системы
со строением человеческой руки.
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Цифры 1,2,3,4,5,6,7,8,9,0 сложились в Индии. Древнейшая запись обнаружена в Индии и датируется 595г.
Древнее изображение десятичных цифр не
случайно: каждая цифра обозначает число по
количеству углов в ней. Например, 0 – углов нет,
2 – два угла и т.д. Написание десятичных цифр претерпело существенные изменения.
Форма, которой мы пользуемся,
установилась в XVI веке.
Индийская нумерация пришла сначала в арабские страны, а потом в Западную Европу. Простые и удобные правила сложения и вычитания очень больших чисел, записанной в этой системе, сделали ее особенно популярной.
Эти правила вывел азиатский математик аль-Хорезми. А поскольку его труд был написан на арабском языке, то и Индийская нумерация в Европе закрепилась неправильным названием «арабское».
ДВЕНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Считали фаланги пальцев на руке кроме большого.
Четыре пальца по три фаланги всего 12.
Элементы двенадцатеричной системы счисления сохранились в Англии в системе мер (1 фут = 12 дюймов) и в денежной системе (1 шиллинг = 12 пенсам).
Нередко и мы сталкиваемся в быту
с двенадцатеричной системой счисления:
чайные и столовые сервизы на 12 персон,
комплект носовых платков – 12 штук.
ДВАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
У ацтеков и майя – народов, населявших в течение многих столетий обширные области Американского континента и создавших там высочайшую культуру, в том числе и математическую, была принята двадцатеричная система счисления.
Начиная со второго тысячелетия да нашей эры также двадцатеричная система счисления была
принята и у кельтов, населявших Западную Европу
Основу для счета в этой системе счисления
составляли пальцы рук и ног.
Некоторые следы двадцатеричной системы счисления кельтов сохранились во французской денежной системе: основная денежная единица, франк, делится на 20
Это первая система счисления, существовавшая в Древнем Вавилоне, за две тысячи лет до н.э., основанная на позиционном принципе. Древние вавилоняне считали продолжительность года равной 360 суткам, что связано с числом 60. Отголоски использования этой системы счисления дошли до наших дней. Например, 1 час = 60 минутам.
Система вавилонян сыграла большую
роль в развитии математики и астрономии,
ее следы сохранились до наших дней.
Так, мы до сих пор делим час на 60 минут,
а минуту на 60 секунд. Точно так же,
следуя примеру вавилонян,
окружность мы делим
на 360 частей (градусов).
Вавилонская табличка с числом 1;24,51,10 — наиболее точным приближением квадратного корня из двух четырьмя шестидесятеричными цифрами.
— это знаковая система, в которой числа записываются по определённым правилам с помощи знаков некоторого алфавита, называемых цифрами.
2. Какие системы счисления вы знаете?
Позиционные и Непозиционные
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.
4. Назовите основание десятичной системы счисления? Двоичной системы счисления?
5.Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления?
6. Чему равны в десятичной системе счисления следующие числа записанные в римской системе счисления: XVIII XXIV MDX
Список источников содержания и иллюстраций