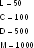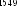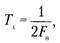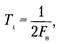кодирование и квантование сигналов

2) Сообщения и сигналы. Кодирование и квантование сигналов.

Сообщение – последовательность сигналов

Сообщение — наименьший элемент языка, имеющий идею или смысл, пригодный для общения. В информатике — форма представления информации, имеющая признаки начала и конца, предназначенная для передачи через среду связи. Также форма предоставления информации, совокупность знаков или первичных сигналов, содержащих информацию.

Чтобы сообщение стало сигналом его необходимо интерпретировать

1) одно и то же сообщение несет различную информацию

2) разные сообщения несут одну и ту же информацию

Сигнал – изменяемая во времени физическая величина

Сигнал (в теории информации и связи) — материальный носитель информации, используемый для передачи сообщений в системе связи. Сигнал может генерироваться, но его приём не обязателен, в отличие от сообщения, которое должно быть принято принимающей стороной, иначе оно не является сообщением. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.

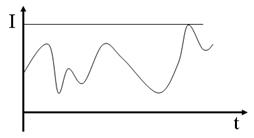
1) АНАЛОГОВЫМназывается сигнал, который может приниматьлюбоезначение на некотором промежутке.

2) ДИСКРЕТНЫМ называется сигнал, который может принимать строго определенные значения на некотором промежутке

Кодирование – преобразование информации в форму, пригодную для передачи по каналу связи.

Декодирование – преобразование информации в форму, пригодную для получения.

Дискретизация— преобразование непрерывной функции в дискретную.

Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизациейиликвантованием по уровню(ср. «Квантование по времени»).

Квантование по уровню широко используется в цифровых автоматах.

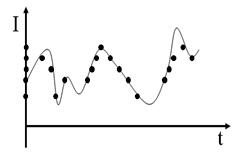
Точки на втором рисунке называется квантованием

Квантование (англ. quantization) — в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей. Простейшим видом квантования является деление целочисленного значения на натуральное число.

3) Позиционные системы счисления. Методы перевода чисел.

Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр.

Виды систем счисления:

Унарной называют систему счисления, в которой для записи чисел используют только один знак – 1 (например, Счетные палочки).

Непозиционной называют систему счисления, в которой значение цифры в изображении числа не зависит от ее положения в ряду других цифр.

Нет 0 и знаков больших М

Неудобно проводить вычисления.

Позиционной называют систему счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Шестидесятеричная и др.

Построение чисел в позиционных системах счисления

Пусть р – основание системы счисления.

Тогда любое число Х можно представить в виде многочлена:

Из коэффициентов строится сокращенная запись числа:

Коэффициенты – целые числа 0≤a_i≤р-1

Каково минимальное значение р?

р = 1 – унарная система счисления.

р = 2 – двоичная система счисления.

Представление чисел в различных системах счисления

Перевод чисел из q-ричной системы счисления в р-ричную

Для замены исходного числа Xqравным ему числомXpнужно по правиламq-ричной арифметики целочисленно делитьXqна новое основание р. Результаты деления, записанные в обратном порядке от последнего к первому, и окажутся цифрамиXp.

Основание системы счисления

Самой экономичной является троичная система счисления

Перевод чисел между системами счисления 2-8-16

Для перевода целого двоичного числа в систему счисления с основанием p=2 r достаточно данное двоичное число разбить справа налево на группы вrцифр каждая и каждую группу независимо перевести в системуp.

Источник

Вопрос №1 «Сигналы; кодирование и квантование сигналов. Системы счисления.»

Отчет по практике задание №22

Студент группы №6116 Чжан А.Ф.

Руководитель Парамонова Надежда Николаевна

Вопрос №1 «Сигналы; кодирование и квантование сигналов. Системы счисления.». 2

Вопрос №2: «Центральный процессор, системные шины.». 7

Вопрос №3: «Понятие системного программного обеспечения: назначение, возможности, структура; операционные системы.». 10

Вопрос №4 «Электронные презентации.». 14

Вопрос №5 «Классификация и формы представления моделей.». 15

Вопрос №6: «Операторы циклов и ветвления.». 19

Вопрос №7: «Основные понятия языков программирования. Развитие языков программирования.». 21

Вопрос №8: «Назначение и основы использования систем искусственного интеллекта; базы знаний, экспертные системы, искусственный интеллект.». 21

Вопрос №9: «Компьютерные коммуникации и коммуникационное оборудование» 22

Вопрос №10: «Информационная безопасность и ее составляющие». 25

Список использованных источников: 30

Вопрос №1 «Сигналы; кодирование и квантование сигналов. Системы счисления.»

Физические сигналы являются непрерывными функциями времени. Чтобы преобразовать непрерывный, в частности, аналоговый сигнал в цифровую форму используются аналого-цифровые преобразователи (АЦП). Процедуру аналого-цифрового преобразования сигнала обычно представляют в виде последовательности трех операций: дискретизации, квантования и кодирования.

В технических кодах буквы, цифры и другие знаки почти всегда кодируются двоичными последовательностями, называемыми двоичными кодовыми словами.

Широко используются двоичные коды:

Оба этих кода включают битовые комбинации для печатаемых символов и некоторых распространенных командных слов типа NUL, CR, ACK, NAK и др.

Асинхронное и синхронное кодирование. Для правильного распознавания позиций символов в передаваемом сообщении получатель должен знать границы передаваемых элементов сообщения. Для этого необходима синхронизация передатчика и приемника. Использование специального дополнительного провода для сигналов синхронизации (в этом случае имеем битовую синхронизацию) слишком дорого, поэтому используют другие способы синхронизации.

В синхронном режиме синхронизм поддерживается во время передачи всего информационного блока без обрамления каждого байта. Такие коды называют бит-ориентированными. Для входа в синхронизм нужно обозначать границы лишь всего передаваемого блока информации с помощью специальных начальной и конечной комбинаций байтов (обычно это двубайтовые комбинации). В этом случае синхронизация называется блочной (фреймовой).

Для обрамления текстового блока (текст состоит только из печатаемых символов) можно использовать символы, отличающиеся от печатаемых. Для обрамления двоичных блоков применяют специальный символ (обозначим его DLE), который благодаря стаффингу становится уникальным. Уникальность заключается в том, что если DLE встречается внутри блока, то сразу вслед за ним вставляется еще один DLE. Приемник будет игнорировать каждый второй идущий подряд символ DLE. Если же DLE встречается без добавления, то это граница блока.

· возможность представления любого числа в рассматриваемом диапазоне величин;

· единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

· простоту оперирования числами;

В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные. Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа (римская система счисления). Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.

Источник

Сигналы; кодирование и квантование сигналов. Системы счисления

Сигнал является материальным носителем информации, которая передается от источника к потребителю.

Обуславливая диалектическое единство данных и методов в информационном процессе, определяют следующие понятия.

Динамический характер информации. Данные имеют статичный характер. Информация динамически меняется и существует только в момент времени взаимодействия данных и методов. Таким образом, информация существует только в момент протекания информационного процесса. Все остальное время она содержится в виде данных.

Требования адекватности методов. Одни и те же данные могут в момент потребления поставлять разную информацию, в зависимости от степени адекватности взаимодействующих с ними методов. Использование более адекватных методов даст более полную информацию.

Диалектический характер взаимодействия данных и методов. Данные являются объективными, это результат регистрации объективно существовавших сигналов, вызванных изменениями в материальных полях или телах. В тоже время методы являются субъективными. В основе искусственных методов лежит алгоритм, т.е. упорядоченная последовательность команд, составленная и подготовленная человеком (субъектом). В основе естественных методов лежат биологические свойства субъектов информационного процесса.

Таким образом, информация возникает и существует в момент диалектического взаимодействия объективных данных и субъективных методов.

Для автоматизации работы с данными, относящимися к различным типам и несущим в себе различную информацию очень важно унифицировать форму их представления. Для этого обычно используется прием кодирования.

В вычислительной технике работа ведется с числовой информацией. Остальная информация тексты, звуки, изображения и т.д. для обработки в вычислительной среде должна быть преобразована в числовую форму. При этом все числа в память компьютера записываются с использованием, так называемого двоичного кодирования. Двоичное кодирование основано на представлении данных последовательностью всего двух знаков 0 и 1. Эти знаки называются двоичными цифрами, по-английски binary digit или сокращенно (bit) бит.

Двоичная система кодирования выбрана совсем не случайно. Она легко реализуется технически. Электронные схемы для обработки двоичных кодов должны находиться в одном из двух состояний «есть сигнал/нет сигнала» или «высокое / низкое» напряжение и т.д. Схему легко переключать из одного состояния в другое.

Группа из восьми бит называется байт и обеспечивает основу записи информации в память компьютера.

Для правильного понимания, как представляется информации в памяти компьютера, рассмотрим различные системы счисления, используемые современными вычислительными средствами.

Системы счисления бывают позиционные и непозиционные.

В общем виде целое число в позиционной системе счисления можно представить выражением:

N (m) = k0 * m0 + k1 * m1 +…kn-1 * mn-1, где

Рассмотрим, как записываются числа в позиционных системах счисления, используемых современной вычислительной техникой.

Десятичная система счисления.

N(10) = 7*100 + 5*101 + 9*102 + 1*103 = 1957

Двоичная система счисления.

N(2) = 1*20 + 1*21 + 0*22 + 0*23 + 0*24 + 1*25 = 35, т.е. двоичное число 100011В = десятичному числу 35.

Обратим внимание, что для записи чисел в позиционных системах счисления могут быть использованы одинаковые цифры. Так цифры 0 и 1 используются как десятичной, так и двоичной системой. Поэтому в записи чисел недесятичной системы счисления принято использовать буквы являющиеся идентификаторами систем счисления и позволяющие отличить числа одной системы счисления от другой.

Восьмеричная система счисления

N(8) = 3*80 + 7*81 + 5*82 = 379, т.е. восьмеричное число 573Q = десятичному числу 379.

Шестнадцатеричная система счисления.

N(16) = 7*160 + 10*161 + 1*162 = 423, т.е. шестнадцатеричное число 1A7H = десятичному числу 423.

Каждый раз, вычисляя число N(m) по приведенной выше формуле мы получаем число в десятичной системе. Таким образом, числа из 2-ой, 8-ой и 16-ой системы мы переводили в десятичную систему счисления.

Источник

Кодирование и квантование сигналов

При использовании ЭВМ для обработки информации от различных устройств (объектов, процессов), в которых информация представлена непрерывными (аналоговыми) сигналами, требуется преобразовать аналоговый сигнал в цифровой — в число, пропорциональное амплитуде этого сигнала, и наоборот. В общем случае процедура аналого-цифрового преобразования состоит из трех этапов:

квантования по уровню;

Под дискретизацией понимают преобразование функции непрерывного времени в функцию дискретного времени, а сам процесс дискретизации состоит в замене непрерывной функции её отдельными значениями в фиксированные моменты времени.

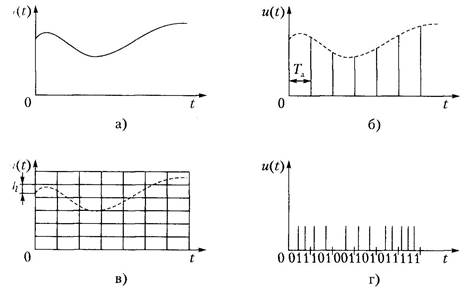
Дискретизация может быть равномерной и неравномерной. При неравномерной дискретизации длительность интервалов между отсчетами различна. Наиболее часто применяется равномерная дискретизации, при которой длительность интервала между отсчетами ТД, постоянна. Период дискретизации ТД непрерывного сигнала и(t) (рис. 1 а) выбирается в соответствии с теоремой Котельникова:

где Fв — высшая частота в спектре частот сигнала и(t) (рис. 1 б)

Рис. 1.Процесс аналого-цифрового преобразования

Под квантованием понимают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений.

Для этого весь диапазон значений сигнала и(t), называемый шкалой делится на равные части – кванты, h – шаг квантования. Процесс квантования сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования.

Вид сигнала и(t) в результате совместного проведения операций дискретизации и квантования представлен на рис. 1 в). Дискретизированное значение сигнала и(t), находящееся между двумя уровнями квантования, отождествляется с ближайшим уровнем квантования. Это приводит к ошибкам квантования, которые всегда меньше шага квантования (кванта), т. е. чем меньше шаг квантования, тем меньше погрешность квантования, но больше уровней квантования.

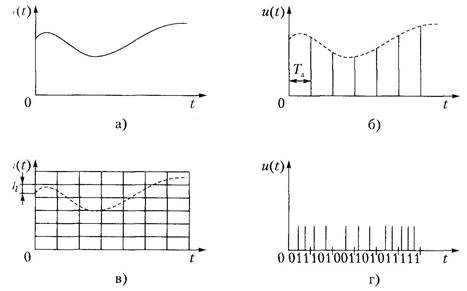
Число уровней квантования на рис. 1 в) равно восьми. Обычно их значительно больше. Можно провести нумерацию уровней и выразить их в двоичной системе счисления. Для восьми уровней достаточно трех двоичных разрядов. Каждое дискретное значение сигнала представляется в этом случае двоичным кодом (табл. 1) в виде последовательности сигналов двух уровней.

Наличие или отсутствие импульса на определенном месте интерпретируется единицей или нолем в соответствующем разряде двоичного числа. Цифровая форма представления сигнала и(t) показана на рис. 1 г). Импульсы старших разрядов расположены крайними справа.

Таким образом, в результате дискретизации, квантования и кодирования аналогового сигнала получаем последовательность n-разрядных кодовых комбинаций, которые следуют с периодом дискретизации Тл. При этом рациональное выполнение операций дискретизации и квантования приводит к значительному экономическому эффекту как за счет снижения затрат на хранение и обработку получаемой информации, так и вследствие сокращения времени обработки информации.

На практике преобразование аналогового сигнала в цифровую форму осуществляется с помощью аналого-цифрового преобразователя (АЦП). Для решения обратной задачи преобразования числа в пропорциональную аналоговую величину, представленную в виде электрического напряжения, тока и т. п., служит цифроаналоговый преобразователь (ЦАП). В ЦАП каждая двоичная кодовая комбинация преобразуется в аналоговый сигнал, и на выходе создается последовательность модулированных по амплитуде импульсов с периодом Тл.

Статьи к прочтению:

От аналоговых сигналов к цифре

Похожие статьи:

Вопрос №1 Информатика– наука, изучающая структуру и свойства информации, а также вопросы, связанные с ее сбором, хранением, обработкой, передачей и…

ПРАКТИЧЕСКАЯ РАБОТА 2 Тема: Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации 1. Цель работы:изучить…

Источник

Кодирование и квантование сигналов

При использовании ЭВМ для обработки информации от различных устройств (объектов, процессов), в которых информация представлена непрерывными (аналоговыми) сигналами, требуется преобразовать аналоговый сигнал в цифровой — в число, пропорциональное амплитуде этого сигнала, и наоборот. В общем случае процедура аналого-цифрового преобразования состоит из трех этапов:

квантования по уровню;

Под дискретизацией понимают преобразование функции непрерывного времени в функцию дискретного времени, а сам процесс дискретизации состоит в замене непрерывной функции её отдельными значениями в фиксированные моменты времени.

Дискретизация может быть равномерной и неравномерной. При неравномерной дискретизации длительность интервалов между отсчетами различна. Наиболее часто применяется равномерная дискретизации, при которой длительность интервала между отсчетами Т_Д, постоянна. Период дискретизации Т_Д непрерывного сигнала и(t) (рис. 1 а) выбирается в соответствии с теоремой Котельникова:

Рис. 1.Процесс аналого-цифрового преобразования

Под квантованием понимают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений.

Для этого весь диапазон значений сигнала и(t), называемый шкалой делится на равные части – кванты, h – шаг квантования. Процесс квантования сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования.

Вид сигнала и(t) в результате совместного проведения операций дискретизации и квантования представлен на рис. 1 в). Дискретизированное значение сигнала и(t), находящееся между двумя уровнями квантования, отождествляется с ближайшим уровнем квантования. Это приводит к ошибкам квантования, которые всегда меньше шага квантования (кванта), т. е. чем меньше шаг квантования, тем меньше погрешность квантования, но больше уровней квантования.

Число уровней квантования на рис. 1 в) равно восьми. Обычно их значительно больше. Можно провести нумерацию уровней и выразить их в двоичной системе счисления. Для восьми уровней достаточно трех двоичных разрядов. Каждое дискретное значение сигнала представляется в этом случае двоичным кодом (табл. 1) в виде последовательности сигналов двух уровней.

Наличие или отсутствие импульса на определенном месте интерпретируется единицей или нолем в соответствующем разряде двоичного числа. Цифровая форма представления сигнала и(t) показана на рис. 1 г). Импульсы старших разрядов расположены крайними справа.

Таким образом, в результате дискретизации, квантования и кодирования аналогового сигнала получаем последовательность n-разрядных кодовых комбинаций, которые следуют с периодом дискретизации Т_л. При этом рациональное выполнение операций дискретизации и квантования приводит к значительному экономическому эффекту как за счет снижения затрат на хранение и обработку получаемой информации, так и вследствие сокращения времени обработки информации.

На практике преобразование аналогового сигнала в цифровую форму осуществляется с помощью аналого-цифрового преобразователя (АЦП). Для решения обратной задачи преобразования числа в пропорциональную аналоговую величину, представленную в виде электрического напряжения, тока и т. п., служит цифроаналоговый преобразователь (ЦАП). В ЦАП каждая двоичная кодовая комбинация преобразуется в аналоговый сигнал, и на выходе создается последовательность модулированных по амплитуде импульсов с периодом Т_л.

Источник