квадратные неравенства примеры для тренировки
Квадратные неравенства примеры для тренировки
На каком рисунке изображено множество решений неравенства
В ответе укажите номер правильного варианта.
Решим неравенство:   Корнями уравнения
являются числа 1 и 3. Поэтому
Множество решений неравенства изображено на рис. 1.
Правильный ответ указан под номером 1.
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решим каждое из неравенств.
1)   — решений нет.
2)  
3)   верно для всех
4)  
На рисунке изображено решение четвёртого неравенства.
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения.
Алгоритм решения квадратного неравенства методом интервалов
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим квадратное неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
Решение:
Приводим квадратное неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Решение:
Приводим квадратное неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x 6.
Решение:
Приводим квадратное неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
№5. Решить неравенство x 2 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Квадратные неравенства
Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.
В зависимости от значения a ветви графика направлены вверх или вниз:
Квадратные неравенства имеют вид.
ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0
Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?
Как решать квадратные неравенства?
Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Пример:
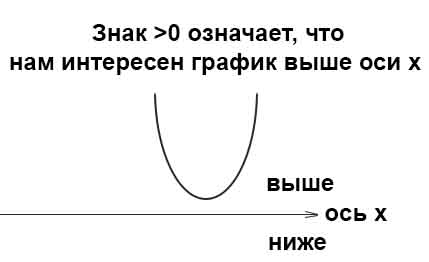
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.
Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.
Пример:
Рассмотрим этот же пример со знаком неравенства меньше 0
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.
А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.
Второй участок (-2; 1). На этом участке можно взять число 0.
Третий участок (1; +∞). На этом участке возьмем число 2.
Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.
Квадратные неравенства, примеры, решения
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Приведем пример квадратного неравенства:
Или вот такое неравенство:
Покажем несколько примеров квадратных неравенств:
Способы решения квадратных неравенств
Основным метода три:
Графический метод
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.
Выделение квадрата двучлена
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14
Метод интервалов, решение неравенств
Определение квадратного неравенства
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
Квадратное неравенство можно решить двумя способами:
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком