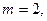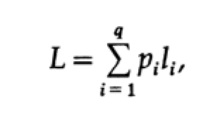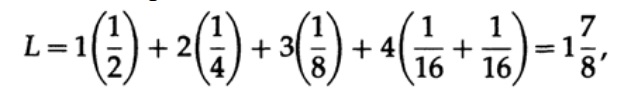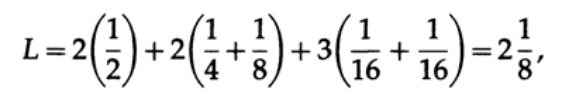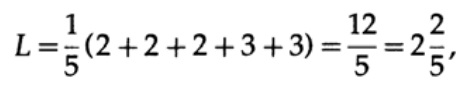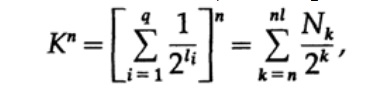основные понятия теории кодирования
Основные понятия теории кодирования
, (1.1)
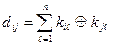
где 
и 
— одноименные (
ые) разряды кодовых слов 
и 
, соответственно. Так, 
, 
, 
и 
при 
. Для двоичного кода расстояние 
равно числу разрядов, в которых слова и различны. Кодовое расстояние 
— наименьшее для данного кода значение . В эквидистантном коде расстояния между двумя любыми его словами одинаковы. Число ненулевых элементов кодового слова равно его весу 
.
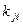
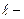
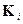
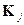
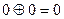
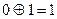
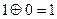
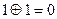
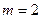
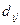
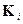
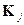
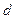
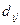
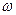
1.2. Классификация методов кодирования
1) приемник может восстановить сообщение источника, посланное по линии связи;
2) для представления одного сообщения в среднем нужно минимальное число символов.
Первому требованию удовлетворяют обратимые коды. В них все кодовые слова различны и однозначно связаны с соответствующими сообщениями. Экономные коды удовлетворяют второму требованию.
 |
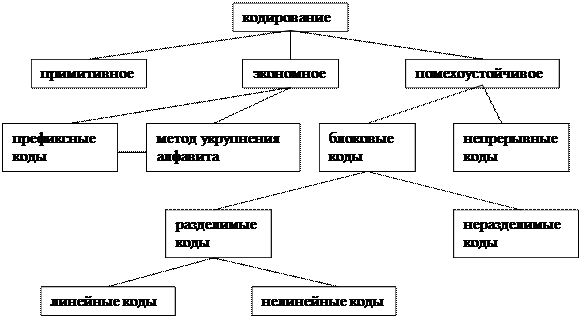Рис. 1.1. Классификация методов кодирования
Коды бывают первичные (простые или примитивные) и помехоустойчивые. Простые коды состоят из всех кодовых слов, возможных при данном способе кодирования. Превращение одного символа кодового слова в другое из-за действия помех дает новое кодовое слово. Возникает ошибка, которую нельзя обнаружить. В помехоустойчивых кодах применяют лишь часть из общего числа возможных кодовых слов. Применяемые слова называют разрешенными, остальные – запрещенными. Помехоустойчивое кодирование позволяет повысить верность передачи сообщений.
Различают кодирующие устройства (кодеры) для источника информации и для канала связи. Задачей первого является экономное (в смысле минимума среднего числа символов) представление сообщений, а задачей второго – обеспечение достоверной передачи сообщений.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Декодирующее устройство (декодер) вместе с кодером образует кодек. Обычно кодек – логическое устройство.
Помехоустойчивое (избыточное) кодирование применяют для обнаружения и исправления ошибок, возникающих при передаче сообщения по каналу. Тогда избыточность источника, образованного выходом кодера, больше избыточности источника на входе кодера. Это кодирование распространено в разных системах связи, при хранении и передаче данных в сетях ЭВМ, в цифровой аудио- и видеотехнике.
Пример 1.2.1.Примитивным равномерным кодом, используемым в телеграфии, является код Бодо с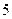 
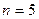
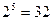
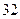
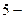
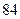
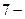
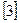
двоичными элементами в каждом слове (
). Полное число слов 
. Этого достаточно для кодирования 
букв русского алфавита, но недостаточно для передачи сообщения, содержащего буквы, цифры и разные условные знаки (точка, запятая, сложение, умножение и т.п.). Тогда можно применить ²Международный код №2² (МТК-2) с регистровым принципом. В нем одно и то же 
элементное кодовое слово можно использовать до трех раз в зависимости от положения регистра: русский, латинский и цифровой. Общее число разных знаков равно 
, что достаточно для кодирования телеграммы. Для передачи данных рекомендован 
элементный код МТК-5 
.
В неравномерных кодах кодовые слова различаются не только расположением символов, но и их числом. Эти коды требуют либо специальных разделительных знаков, указывающих конец одного и начало другого кодового слова, либо строятся так, чтобы никакое кодовое слово не было началом другого. Префиксные (неприводимые) коды удовлетворяют последнему условию. Заметим, что равномерный код является неприводимым.
Пример 1.2.3.Пусть алфавит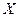 
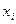
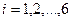
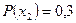
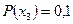
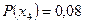
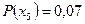
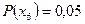
источника состоит из символов 
, 
. Вероятности появления символов на выходе источника, соответственно, равны 
, 
, 
, 
, 
и 
. Процедура Шеннона-Фано построения неравномерного кода без укрупнения алфавита источника задается табл. 1.1 
.
Таблица 1.1. Кодирование источника по методу Шеннона-Фано
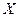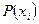| |  | Выбор символов неравномерного кода |  |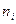
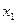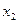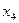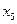      | 0,4 0,3 0,1 0,08 0,07 0,05 |
Непрерывное кодирование и декодирование делают над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных наиболее часто применяют сверточные коды (см. п. 6.8).
Различают каналы связи с независимыми и группирующимися ошибками. Соответственно, помехоустойчивые коды можно разбить на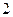 
класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Для исправления последних есть много эффективных кодов. На практике целесообразнее применять коды, исправляющие независимые ошибки, вместе с устройством перемежения символов (декорреляции ошибок). Тогда символы кодового слова не передаются последовательно, а перемешиваются с символами других кодовых слов. Если интервал между символами каждого кодового слова сделать больше ²памяти² канала, ошибки в пределах одного слова станут независимыми. Это и позволяет применять коды, исправляющие независимые ошибки.
В Приложении проиллюстрированы принципы построения кодов и сжатия данных на примере компьютерных сетей.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Ричард Хэмминг: Глава 10. Теория кодирования — I
«Цель этого курса — подготовить вас к вашему техническому будущему.»
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 28 (из 30) глав. И ведем работу над изданием «в бумаге».
Теория кодирования — I
Рассмотрев компьютеры и принцип их работы, сейчас мы будем рассматривать вопрос представления информации: как компьютеры представляют информацию, которую мы хотим обработать. Значение любого символа может зависит от способа его обработки, у машины нет никакого определенного смысла у используемого бита. При обсуждении истории программного обеспечения 4 главе мы рассматривали некоторый синтетический язык программирования, в нём код инструкции останова совпадал с кодом других инструкций. Такая ситуация типична для большинства языков, смысл инструкции определяется соответствующей программой.
Для упрощения проблемы представления информации рассмотрим проблему передачи информации от точки к точке. Этот вопрос связан с вопросом сохранения информация. Проблемы передачи информации во времени и в пространстве идентичны. На рисунке 10.1 представлена стандартная модель передачи информации.
Рисунок 10.1
Слева на рисунке 10.1 находится источник информации. При рассмотрении модели нам неважна природа источника. Это может быть набор символов алфавита, чисел, математических формул, музыкальных нот, символов, которыми мы можем представить танцевальные движения — природа источника и значение хранящихся в нём символов не является частью модели передачи. Мы рассматриваем только источник информации, с таким ограничением получается мощная, общая теория, которую можно распространить на многие области. Она является абстракцией из многих приложений.
Когда в конце 1940 годов Шеннон создал теорию информации, считалось, что она должна была называться теорией связи, но он настоял на термине информация. Этот термин стал постоянной причиной как повышенного интереса, так и постоянных разочарований в теории. Следователи хотели строить целые «теории информации», они вырождались в теории о наборе символов. Возвращаясь к модели передачи, у нас есть источник данных, которые необходимо закодировать для передачи.
Кодер состоит из двух частей, первая часть называется кодер источника, точное название зависит от типа источника. Источникам разных типов данных соответствуют разные типы кодеров.
Вторая часть процесса кодирования называется кодирование канала и зависит от вида канала для передачи данных. Таким образом, вторая часть процесса кодирования согласована с типом канала передачи. Таким образом, при использовании стандартных интерфейсов данные из источника в начале кодируются согласно требованиям интерфейса, а потом согласно требованиям используемого канала передачи данных.
Согласно модели, на рисунке 10.1 канал передачи данных подвергается воздействию «дополнительного случайного шума». Весь шум в системе объединен в этой точке. Предполагается, что кодер принимает все символы без искажений, а декодер выполняет свою функцию без ошибок. Это некоторая идеализация, но для многих практических целей она близка к реальности.
Фаза декодирования также состоит из двух этапов: канал — стандарт, стандарт- приемник данных. В конце передачи данных передаются потребителю. И снова мы не рассматриваем вопрос, как потребитель трактует эти данные.
Как было отмечено ранее, система передачи данных, например, телефонных сообщений, радио, ТВ программ, представляет данные в виде набора чисел в регистрах вычислительной машины. Повторю снова, передача в пространстве не отличается от передачи во времени или сохранения информации. Есть ли у вас есть информация, которая потребуется через некоторое время, то ее необходимо закодировать и сохранить на источнике хранения данных. При необходимости информация декодируется. Если система кодирования и декодирования одинаковая, мы передаем данные через канал передачи без изменений.
Фундаментальная разница между представленной теорией и обычной теорией в физике — это предположение об отсутствии шума в источнике и приемнике. На самом деле, ошибки возникают в любом оборудовании. В квантовой механике шум возникает на любых этапах согласно принципу неопределённости, а не в качестве начального условия; в любом случае, понятие шума в теории информации не эквивалентно аналогичному понятию в квантовой механике.
Для определенности будем далее рассматривать бинарную форму представления данных в системе. Другие формы обрабатываются похожим образом, для упрощения не будем их рассматривать.
Начнем рассмотрение систем с закодированными символами переменной длины, как в классическом коде Морзе из точек и тире, в котором часто встречающиеся символы — короткие, а редкие — длинные. Такой подход позволяет достичь высокой эффективности кода, но стоит отметить, что код Морзе — тернарный, а не бинарный, так как в нём присутствует символ пробела между точками и тире. Если все символы в коде одинаковой длины, то такой код называется блочным.
Первое очевидное необходимое свойство кода — возможность однозначно декодировать сообщение при отсутствии шума, по крайней мере, это кажется желаемым свойством, хотя в некоторых ситуациях этим требованием можно пренебречь. Данные из канала передачи для приемника выглядят как поток символов из нулей и единичек.
Будем называть два смежных символа двойным расширением, три смежных символ тройным расширением, и в общем случае если мы пересылаем N символов приемник видит дополнения к базовому коду из N символов. Приемник, не зная значение N, должен разделить поток в транслируемые блоки. Или, другими словами, у приемника должна быть возможность выполнить декомпозицию потока единственным образом для того, чтобы восстановить исходное сообщение.
Рассмотрим алфавит из небольшого числа символов, обычно алфавиты намного больше. Алфавиты языков начинается от 16 до 36 символов, включая символы в верхнем и нижнем регистре, числа знаки, препинания. Например, в таблице ASCII 128 = 2^7 символов.
Рассмотрим специальный код, состоящий из 4 символов s1, s2, s3, s4
s1 = 0; s2 = 00; s3 = 01; s4 = 11.
Как приёмник должен трактовать следующее полученное выражение
Как s1s1s4 или как s2s4?
Вы не можете однозначно дать ответ на этот вопрос, этот код однозначно нет декодируется, следовательно, он неудовлетворительный. С другой стороны, код
s1 = 0; s2 = 10; s3 = 110; s4 = 111
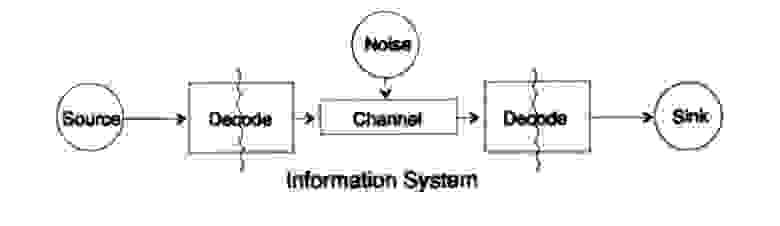
декодирует сообщение уникальным способом. Возьмем произвольную строку и рассмотрим, как ее будет декодировать приемник. Вам необходимо построить дерево декодирования Согласно форме на рисунке 10.II. Строка
может быть разбита на блоки символов
110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110,…
согласно следующему правилу построения дерева декодирования:
Если вы находитесь в вершине дерева, то считываете следующий символ. Когда вы достигаете листа дерева, вы преобразовывает последовательность в символ и возвращайтесь назад на старт.
Причина существования такого дерева в том, что ни один символ не является префиксом другого, поэтому вы всегда знаете, когда необходимо вернуться в начало дерево декодирования.
Необходимо обратить внимание на следующее. Во-первых, декодирование строго поточный процесс, при котором каждый бит исследуется только однажды. Во-вторых, в протоколах обычно включаются символы, которые являются маркером окончания процесса декодирования и необходимы для обозначения конца сообщения.
Отказ от использования завершающего символа является частой ошибкой при дизайне кодов. Конечно же можно предусмотреть режим постоянного декодирования, в этом случае завершающая символ не нужен.
Следующий вопрос — это коды для поточного (мгновенного) декодирования. Рассмотрим код, который получается из предыдущего отображением символов
s1 = 0; s2 = 01; s3 = 011; s4 = 111.
Предположим мы получили последовательность 011111. 111. Единственный способ, которым можно декодировать текст сообщения: группировать биты с конца по 3 в группе и выделять группы с ведущим нулем перед единичками, после этого можно декодировать. Такой код декодируемый единственным способом, но не мгновенным! Для декодирования необходимо дождаться окончания передачи! В практике такой подход нивелирует скорость декодирования (теорема Макмиллана), следовательно, необходимо поискать способы мгновенного декодирования.
Рассмотрим два способа кодирования одного и того же символа, Si:
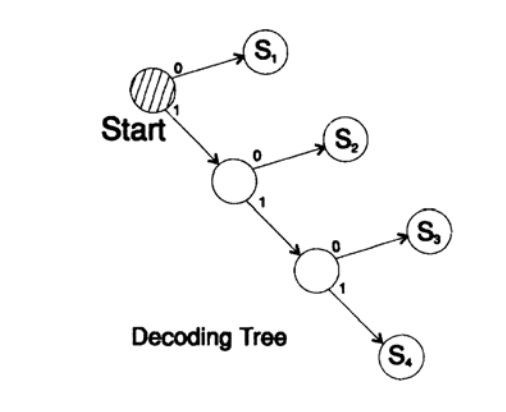
s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,
Дерево декодирование этого способа представлено на рисунке 10.III.
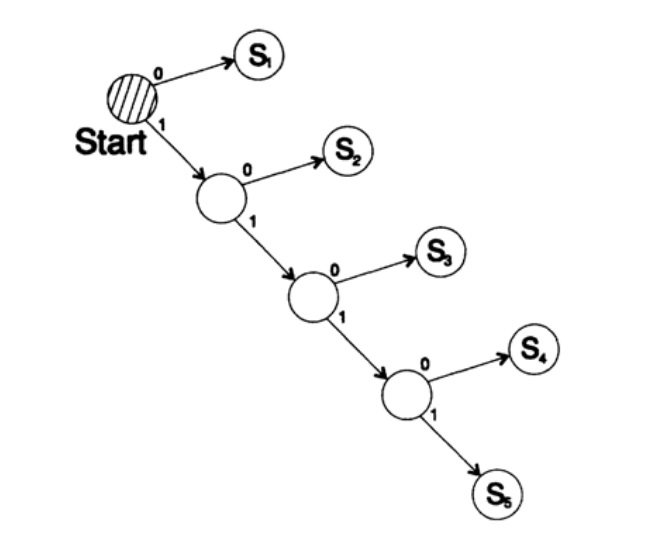
s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111,
Дерево декодирование это ухода представлены на рисунке 10.IV.
Наиболее очевидным способом измерения качество кода — это средняя длина для некоторого набора сообщений. Для этого необходимо вычислить длину кода каждого символа, помноженную на соответствующую вероятность появления pi. Таким образом получится длина всего кода. Формула средней длины L кода для алфавита из q символов выглядит следующим образом
где pi — вероятность появления символа si, li — соответствующая длина закодированного символа. Для эффективного кода значение L должно быть как можно меньше. Если P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 и p5 = 1/16, тогда для кода #1 получаем значение длины кода
Полученные значения говорят о предпочтительности первого кода.
Если у всех слов в алфавите будет одинаковая вероятность возникновения, тогда более предпочтительным будет второй код. Например, при pi = 1/5 длина кода #1
этот результат показывает предпочтительность 2 кода. Таким образом, при разработке «хорошего» кода необходимо учитывать вероятность возникновения символов.
Рассмотрим неравенство Крафта, которое определяет предельное значение длины кода символа li. По базису 2 неравенство представляется в виде
Это неравенство говорит о том, что в алфавите не может быть слишком много коротких символов, в противном случае сумма будет довольно большой.
Рассмотрим доказательство теорема Макмиллана. Применим неравенство Крафта к непоточно декодируем кодам. Доказательство построено на том факте, что для любого числа K > 1 n-ая степень числа заведомо больше линейной функции от n, где n — довольно большое число. Возведем неравенство Крафта в n-ую степень и представим выражение в виде суммы
где Nk число символов длины k, суммирование начинаем с минимальной длины n-го представление символа и заканчиваем максимальной длины nl, где l — максимальная длина закодированного символа. Из требования уникального декодирования следует, что. Сумма представляется в виде
Если K > 1, тогда необходимо n установить довольно большим для того, чтобы неравенство стало ложным. Следовательно, k Содержание книги и переведенные главы
Есть четыре типа кодирования:
СОДЕРЖАНИЕ
История теории кодирования
Двоичный код Голея был разработан в 1949 году является исправлением ошибок кода способен исправлять до трех ошибок в каждом 24-битовом слове, и обнаружении четвертого.
Исходное кодирование
Определение
Длина кодового слова записывается как
Ожидаемая длина кода
Характеристики
Принцип
Пример
Кодирование каналов
На компакт-дисках используется кодирование Рида – Соломона с перекрестным чередованием для распределения данных по диску.
Хотя это не очень хороший код, простой повторяющийся код может служить понятным примером. Предположим, мы берем блок битов данных (представляющий звук) и отправляем его три раза. В приемной мы рассмотрим все три повтора по крупицам и возьмем большинство голосов. Суть в том, что мы не просто отправляем биты по порядку. Мы их чередуем. Блок битов данных сначала делится на 4 меньших блока. Затем мы циклически перебираем блок и отправляем один бит из первого, затем второй и т. Д. Это делается трижды, чтобы распределить данные по поверхности диска. В контексте простого повторяющегося кода это может показаться неэффективным. Однако известны более мощные коды, которые очень эффективны при исправлении «всплеска» ошибки царапины или пятна пыли при использовании этого метода перемежения.
Линейные коды
Термин « алгебраическая теория кодирования» обозначает подполе теории кодирования, в которой свойства кодов выражаются в алгебраических терминах, а затем исследуются.
Теория алгебраического кодирования в основном делится на два основных типа кодов:
Линейные блочные коды
Есть много типов линейных блочных кодов, таких как
Сверточные коды
Идея сверточного кода состоит в том, чтобы сделать каждый символ кодового слова взвешенной суммой различных символов входного сообщения. Это похоже на свертку, используемую в системах LTI для нахождения выхода системы, когда вы знаете вход и импульсную характеристику.
Таким образом, мы обычно находим выходной сигнал системного сверточного кодировщика, который представляет собой свертку входного бита, относительно состояний сверточного кодировщика, регистров.
Сверточные коды используются в модемах голосового диапазона (V.32, V.17, V.34) и в мобильных телефонах GSM, а также в устройствах спутниковой и военной связи.