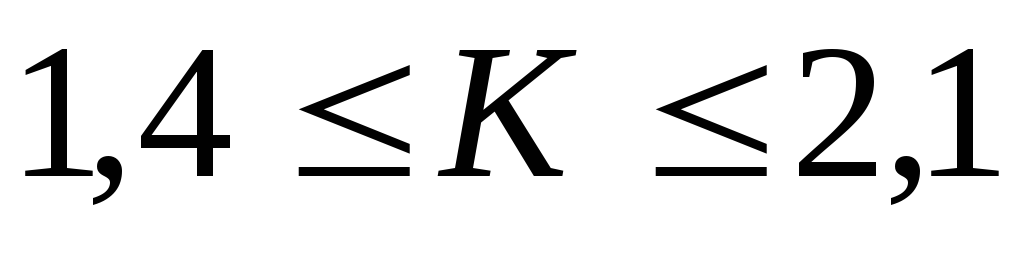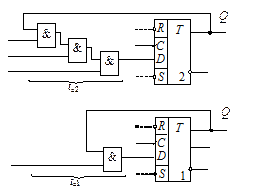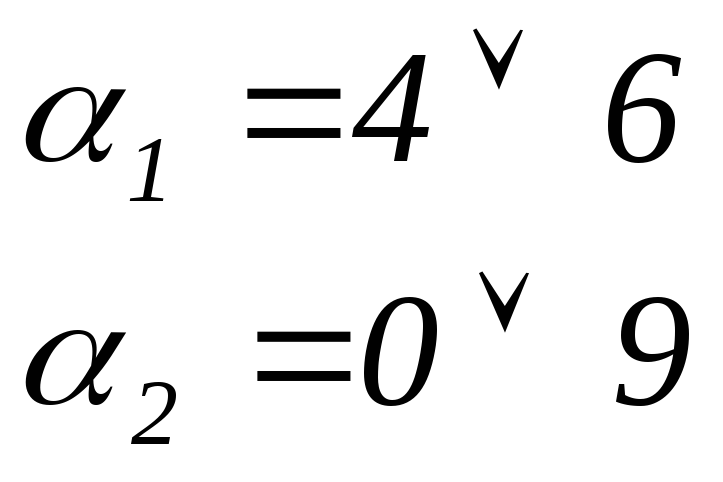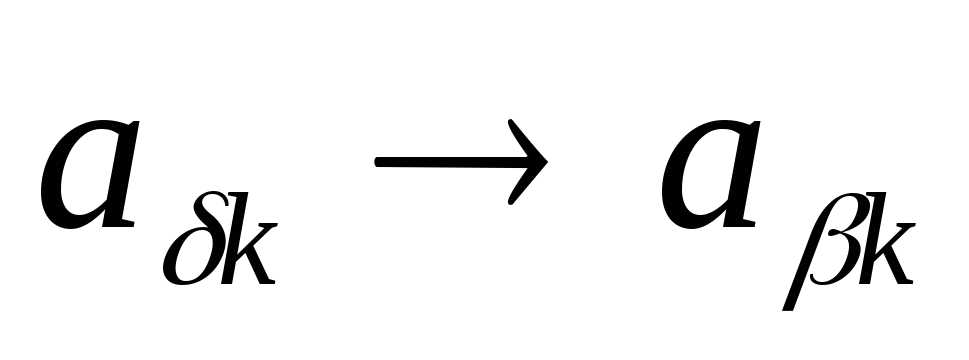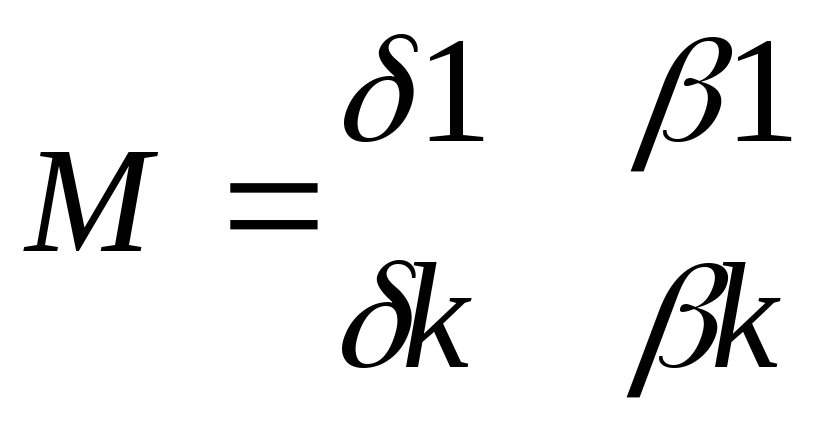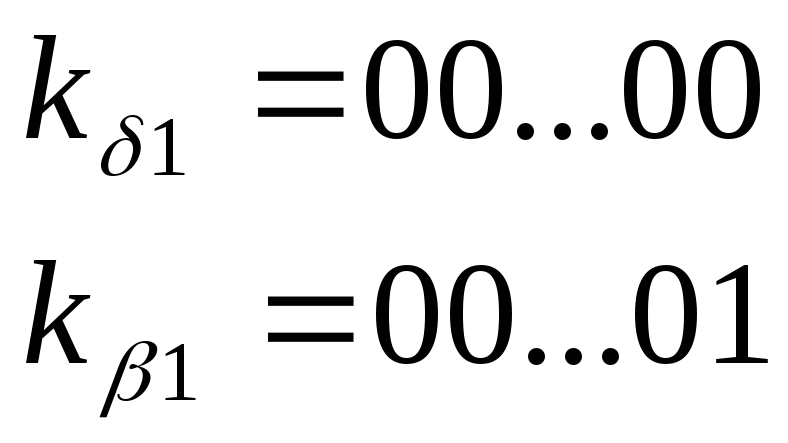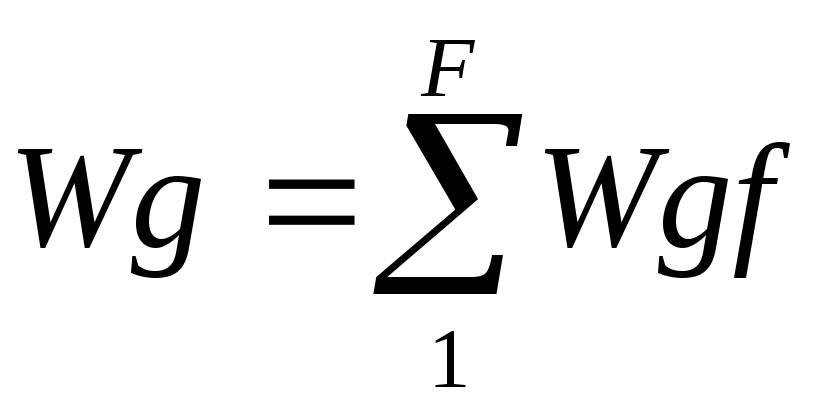с какой целью применяется соседнее кодирование состояний автомата
Соседнее кодирование состояний автомата
Соседними состояниями первого порядка называются состояния, которые можно соединить ребром.
Соседними состояниями первого рода называются состояния, которые под действием одного и того же входного сигнала переходят в одно и то же состояние.
Два состояния, в которые переходят под действием одного и того же входного сигнала состояния, являющиеся соседями первого рода, называются соседями второго рода.
Соседними кодами называются наборы значений, имеющие противоположные значения только в одном разряде, т.е. коды с кодовым расстоянием 1.
При соседнем кодировании любые два состояния, связанные дугой на графе автомата кодируются наборами, отличающимся состоянием лишь одного элемента памяти.
Существуют ограничения соседнего кодирования:
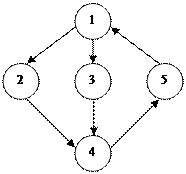
1. В графе автомата не должно быть циклов с нечётным числом вершин.
2. Два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними.
Наиболее просто определить соседей, как первого, так и второго рода, используя обратную таблицу переходов, в отличие от прямой таблицы в её ячейки проставляются состояния, из которых автомат переходит в состояние, указанное в заголовке столбца.
| a1 | a2 | а3 | a4 | a5 | a6 | |
| Z1 | a2 a6 | a1 a4 | — | a3 | — | a5 |
| Z2 | — | — | а1 а3 a4 | — | a2 a5 a6 | — |
Соседями первого рода в обратной таблице переходов оказываются попарно состояния, находящиеся в одной ячейке таблицы:
Соседи второго рода определяются так: если состояния являющиеся соседями первого рода оказались в одной строке, но в разных столбцах, то состояния, соответствующие этим столбцам, будут соседями второго рода.
Часто для кодирования состояний, близких к соседним, используются диаграммы Вейча–Карно. В этом случае первым кодируется состояние, которое в списке соседей встречается наибольшее число раз.
Соседнее кодирование состояний автомата



Соседними состояниями первого порядка называются состояния, которые можно соединить ребром.
Соседними состояниями первого рода называются состояния, которые под действием одного и того же входного сигнала переходят в одно и то же состояние.
Два состояния, в которые переходят под действием одного и того же входного сигнала состояния, являющиеся соседями первого рода, называются соседями второго рода.
Соседними кодами называются наборы значений, имеющие противоположные значения только в одном разряде, т.е. коды с кодовым расстоянием 1.
При соседнем кодировании любые два состояния, связанные дугой на графе автомата кодируются наборами, отличающимся состоянием лишь одного элемента памяти.
Существуют ограничения соседнего кодирования:
1. В графе автомата не должно быть циклов с нечётным числом вершин.
 |
2. Два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними.
 |
Наиболее просто определить соседей, как первого, так и второго рода, используя обратную таблицу переходов, в отличие от прямой таблицы в её ячейки проставляются состояния, из которых автомат переходит в состояние, указанное в заголовке столбца.
| a1 | a2 | а3 | a4 | a5 | a6 | |
| Z1 | a2 a6 | a1 a4 | — | a3 | — | a5 |
| Z2 | — | — | а1 а3 a4 | — | a2 a5 a6 | — |
Соседями первого рода в обратной таблице переходов оказываются попарно состояния, находящиеся в одной ячейке таблицы:
Соседи второго рода определяются так: если состояния являющиеся соседями первого рода оказались в одной строке, но в разных столбцах, то состояния, соответствующие этим столбцам, будут соседями второго рода.
Часто для кодирования состояний, близких к соседним, используются диаграммы Вейча–Карно. В этом случае первым кодируется состояние, которое в списке соседей встречается наибольшее число раз.
Гонки в автомате



Кодирование внутренних состояний ЦА.
Кодирование заключается в сопоставлении каждому состоянию автомата набора (кода) состояний элементов памяти. При этом наборы для всех состояний должны иметь одинаковую длину, а разным состояниям автомата должны соответствовать разные наборы. Если элементы памяти двоичные, то их число 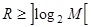


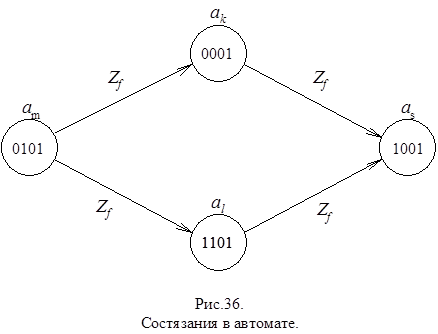 |
Если при переходе автомата из одного состояния в другое должны изменить свои состояния сразу несколько запоминающих элементов, то между ними начинаются состязания. Тот элемент, который выиграет эти состязания, т.е. изменит свое состояние ранее, чем другие элементы, может через цепь обратной связи изменить сигналы на входах некоторых запоминающих элементов до того, как другие, участвующие в состязаниях элементы, изменят свои состояния. Это может привести к переходу автомата в состояние, не предусмотренное его графом. Поэтому в процессе перехода из состояния am в состояние as под действием входного сигнала Zf автомат может оказаться в состоянии ak или al: (рис.36.).
Если затем при том же входном сигнале Zf автомат из аk и аl перейдет в аs, то такие состязания являются допустимыми или некритическими.
Если же в этом автомате есть переход, например, из аk в аj ¹ аs под действием того же сигнала Zf, то автомат может перейти в аj, а не в аs и правильность его работы будет нарушена (рис.37.).
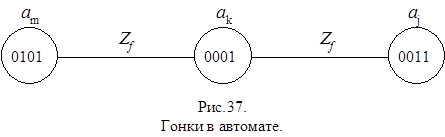 |
Такие состязания называются критическими состязаниями или гонками и необходимо принимать меры для их устранения.
Другой способ ликвидации гонок заключается во введении двойной памяти. В этом случае каждый элемент памяти дублируется, причем перепись из первого элемента памяти во второй происходит в момент С = 0(рис.38.).
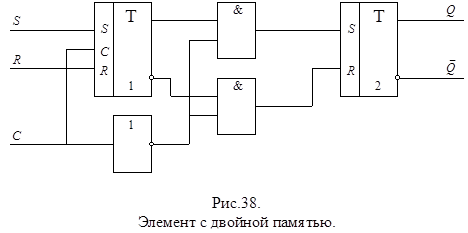 |
Сигналы обратной связи для получения функций возбуждения и функций выходов автомата снимаются с выхода второго триггера. Таким образом состязания могут возникнуть только между первыми триггерами, сигналы ОС (выходы вторых триггеров) не могут измениться до тех пор, пока С не станет равным 0. Но тогда CZf = 0, первый триггер перестанет воспринимать информацию, и гонок не будет.
Для устранения гонок используются специальные методы противогоночного кодирования, среди которых чаще всего применяется так называемое соседнее кодирование состояний автомата, при котором условие отсутствия гонок всегда выполнено. При соседнем кодировании любые два, состояния связанные дугой на графе автомата кодируются наборами, отличающимися состояниями лишь одного элемента памяти.
Соседнее кодирование не всегда возможно. Граф автомата, допускающее соседнее кодирование, должен удовлетворять ряду требований, а именно:
1)в графе автомата не должно быть циклов с нечетным числом вершин;
2)два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними.
 |
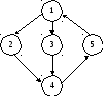
Под состояниями второго порядка понимаются такие два состояния, путь между которыми по графу автомата состоит из двух ребер (независимо от ориентации). Примеры графов автоматов допускающих и не допускающих соседнее кодирование представлены на рис.39а. и 39б. соответственно.
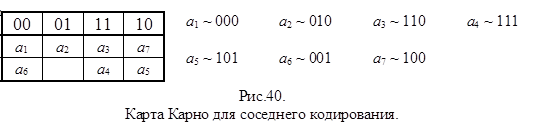 |
При соседнем кодировании обычно пользуются картой Карно. В этом случае состояния, связанные дугой, располагают на соседних клетках карты (рис.40.).
Легко видеть, что при соседнем кодировании на каждом переходе переключается только один триггер, что принципиально устраняет гонки.
Кодирование состояний и сложность комбинационной схемы автомата.
Анализ канонического метода структурного синтеза автомата показывает, что различные варианты кодирования состояний автомата приводят к различным выражениям функций возбуждения памяти и функций выходов, в результате чего сложность комбинационной схемы существенно зависит от выбранного кодирования. Среди множества существующих алгоритмов кодирования рассмотрим лишь два наиболее часто встречаемых:
1)алгоритм кодирования для D-триггеров;
2)эвристический алгоритм кодирования.
Противогоночное кодирование состояний автоматов



При функционировании автомата могут появиться так называемые состязания. Явление состязаний возникает вследствие того, что элементы памяти имеют различные, хотя и достаточно близкие, времена срабатывания. Кроме того, различны также задержки сигналов возбуждения, поступающих по логическим цепям неодинаковой длины td2> td1 (рис. 5.16).
Рисунок 5.16 – Фрагмент схемы автомата
Если при переходе автомата из одного состояния в другое должны изменить свои состояния сразу несколько запоминающих элементов, то между ними начинаются состязания. Тот элемент, который выиграет эти состязания, т.е. изменит свое состояние раньше, чем другие элементы, может через цепь обратной связи изменить сигналы на входах некоторых триггеров до того, как другие триггеры изменят свои состояния. Критические состязания называют гонками.
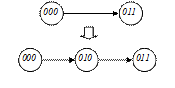
Существуют несколько способов устранения гонок. Когда использовались асинхронные автоматы и синхронные автоматы со статической синхронизацией, был распространен метод противогоночного кодирования, заключающийся в том, что состояния кодировались по возможности соседними кодами, т.е. использовалось соседнее кодирование (чтобы переключался только один триггер), рис. 5.17а. Это не всегда возможно. Или развязывались пары кодов. Т.е. между двумя состояниями, закодированными не соседними кодами, добавлялось состояние с кодом, который был соседним по отношению к этим обоим кодам (рис. 5.17б).
Рисунок 5.17 – Развязывание пар кодов
Это тоже не всегда хорошо, поскольку может привести к появлению нежелательного числа дополнительных состояний.
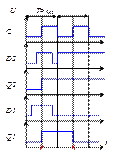
Наилучшим выходом из такого рода проблемы является использование динамически управляемых триггеров. Но и при этом необходимо правильно рассчитать частоту (период) синхросигнала T. Период синхросигнала должен быть больше, чем задержка самой длинной цепи в схеме (сюда входят и задержки элементов, и задержки распространения сигналов по линиям связи), T>td2 рис. 5.18.
Рисунок 5.18 – Выбор периода синхросигнала T
Современные САПР позволяют производить такие расчеты в автоматизированном режиме.
15.2. Соседнее кодирование состояний автомата
Соседними состояниями первого порядка называются состояния, которые можно соединить ребром.
Соседними состояниями первого рода называются состояния, которые под действием одного и того же входного сигнала переходят в одно и то же состояние.
Два состояния, в которые переходят под действием одного и того же входного сигнала состояния, являющиеся соседями первого рода, называются соседями второго рода.
Соседними кодами называются наборы значений, имеющие противоположные значения только в одном разряде, т.е. коды с кодовым расстоянием 1.
При соседнем кодировании любые два состояния, связанные дугой на графе автомата кодируются наборами, отличающимся состоянием лишь одного элемента памяти.
Существуют ограничения соседнего кодирования:
1. В графе автомата не должно быть циклов с нечётным числом вершин.
2. Два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними.
Наиболее просто определить соседей, как первого, так и второго рода, используя обратную таблицу переходов, в отличие от прямой таблицы в её ячейки проставляются состояния, из которых автомат переходит в состояние, указанное в заголовке столбца.
Соседями первого рода в обратной таблице переходов оказываются попарно состояния, находящиеся в одной ячейке таблицы:
Соседи второго рода определяются так: если состояния являющиеся соседями первого рода оказались в одной строке, но в разных столбцах, то состояния, соответствующие этим столбцам, будут соседями второго рода.
Часто для кодирования состояний, близких к соседним, используются диаграммы Вейча–Карно. В этом случае первым кодируется состояние, которое в списке соседей встречается наибольшее число раз.
15.3. Кодирование состояний автомата для минимизации комбинационной схемы
Анализ канонического метода синтеза автомата показывает, что различные варианты кодирования состояний автомата приводят к различным вариантам формирования выражения для функции возбуждения элементов памяти и функции выхода. В результате оказывается, что сложность комбинационной схемы автомата существенно зависит от выбранного кодирования.
Получим отмеченную таблицу переходов структурного автомата:
Возьмём другое кодирование:
При кодировании состояний автомата используются алгоритмы, позволяющие упростить функцию возбуждения элементов памяти, если при синтезе автомата в качестве элементарных автоматов памяти используются D-триггеры.
Алгоритм минимизации при использовании D-триггера.
1. Каждому состоянию ставится в соответствие целое число Nm, равное числу переходов в состояниеаm.
2. Числа Nmсортируются по убыванию.
3. Состояние с наибольшим Nкодируются 00…00.
4. Следующие Iсостояний(I-число ЭП)кодируются 00..01, 00..10..0
5. Для кодирования оставшихся состояний используются коды, содержащие 2, затем 3 единицы и т.д., пока все состояния не будут закодированы.
В результате получаем кодирование, при котором чем больше переходов имеется в некоторое состояние am, тем меньше единиц содержится в его коде.
Большое число работ было посвящено получению такого кодирования, при котором уменьшается зависимость функции возбуждения ЭП от переменных обратной связи 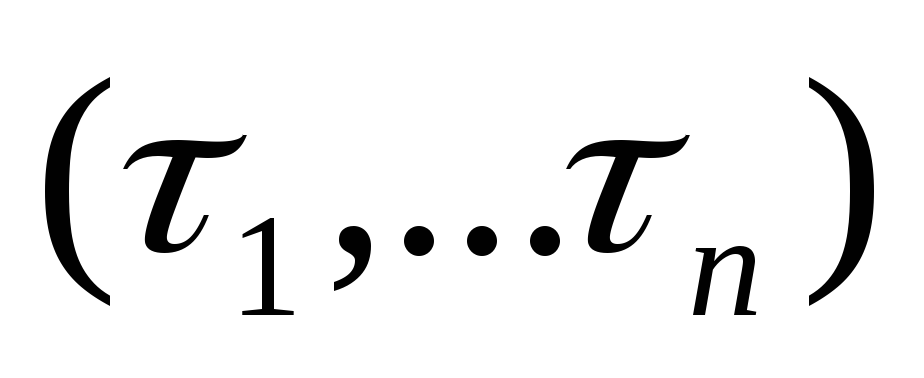
В то же время многие авторы отмечают сложность этих методов кодирования, а также трудности одновременной минимизации функции возбуждения элементов памяти и функции выходов. Поэтому на практике чаще всего используется эвристический алгоритм кодирования состояний автомата, минимизирующий суммарное число переключений элементов памяти на всех переходах автомата. При таком подходе уменьшается сложность схем, реализующих дизъюнкцию на входе ЭП, а, следовательно, минимизирующих и комбинационную схему.
1. Строим матрицу, состоящую из различных пар номеров таких, что в автомате Sесть переход
2. Переставим строки матрицы так, чтобы выполнялось условие:
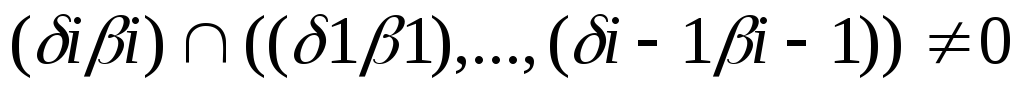
3. Закодируем состояние первой строки:
4. Вычёркиваем из матрицы Мпервую строку. Получим матрицуМ’.
5. В начальной строке матрицы М’один элемент уже закодирован.
6. Выберем незакодированный элемент первой строки матрицы и обозначим его 
Построим матрицу М

7. Пусть множество 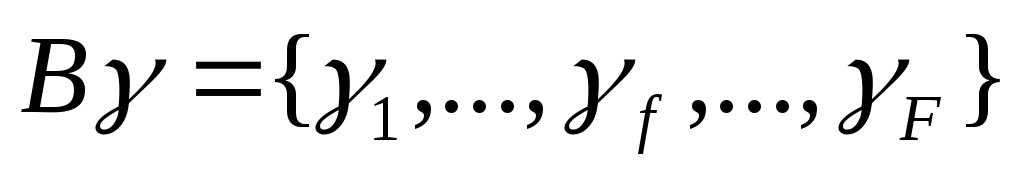

Для каждого кода k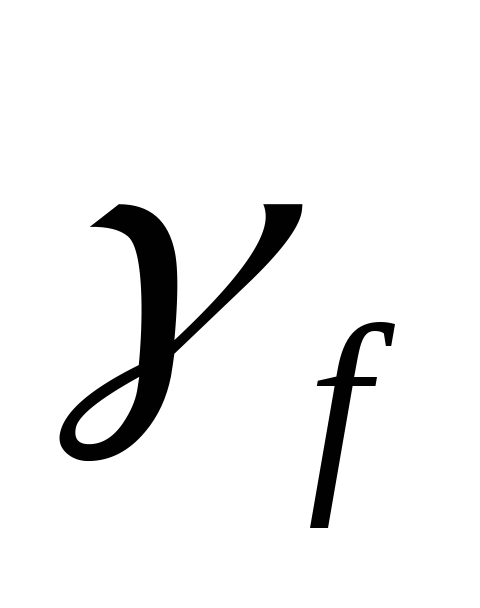
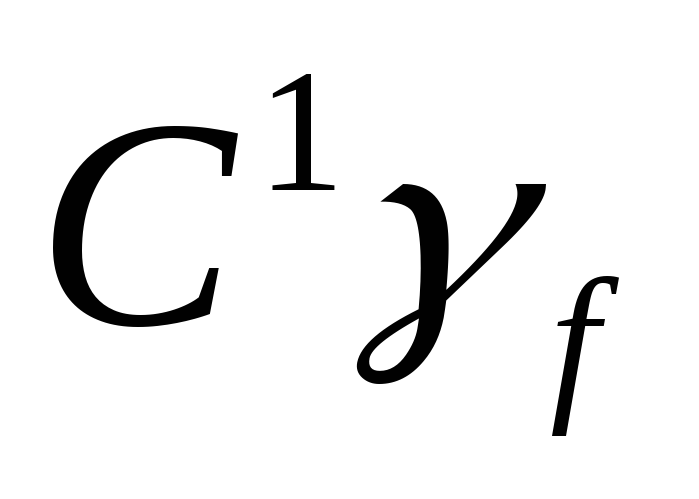
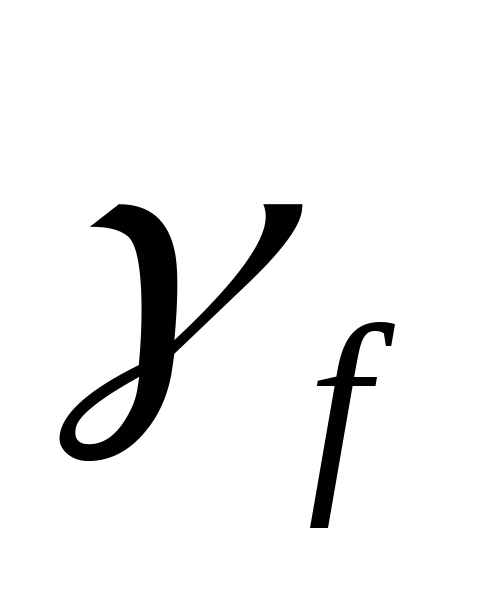
если 
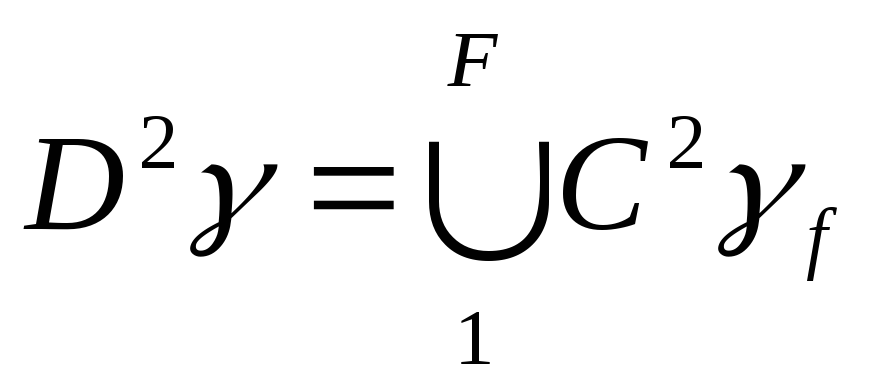
Если нет ни одного множества с незакодированными элементами, то количество ЭП выбрано неправильно.
8. Находим 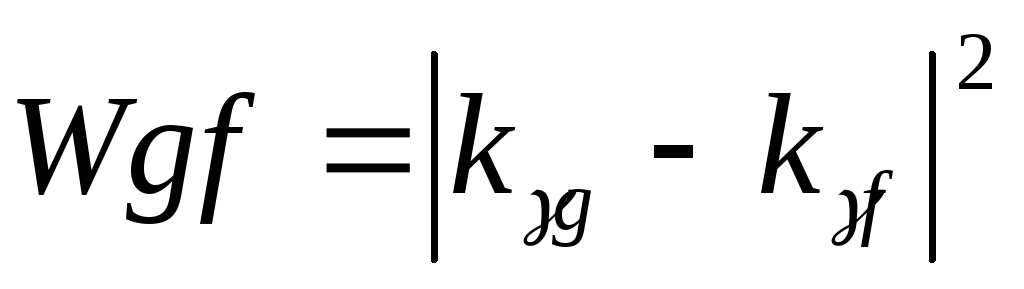
9. Находим сумму всех кодовых расстояний
10. Выбираем код для состояния 
12. Вычисляем 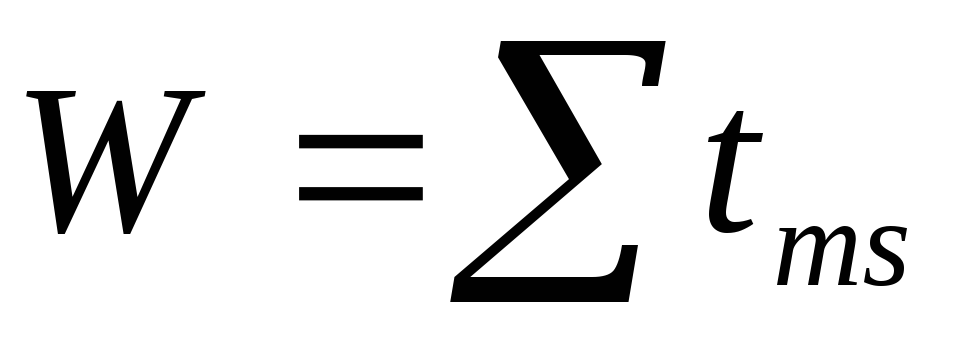
Оценкой качества кодирования рассмотренного алгоритма может служить число К
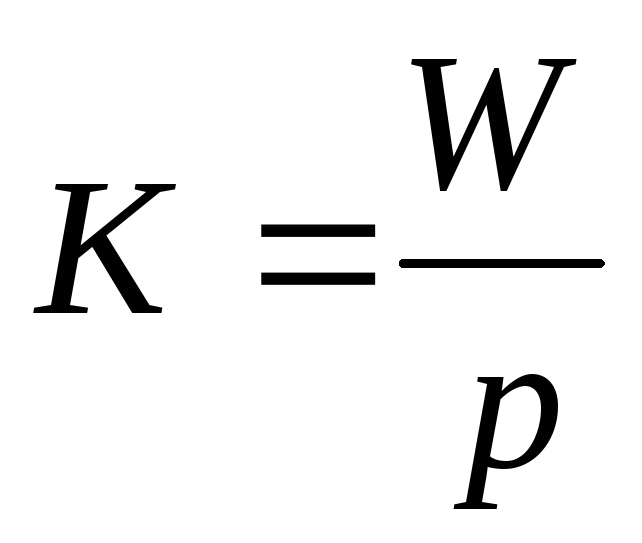
где р— число переходов данного автомата. Чем меньше К, тем ближе полученное кодирование к соседнему.
Эксперименты показали, что Кпри хорошем кодировании лежит в пределах