в каком элементе и на что расходуется энергия в неидеализированном колебательном контуре

Физика. 11 класс

Конспект урока

Урок 7. Свободные и вынужденные электромагнитные колебания. Колебательный контур

Перечень вопросов, рассматриваемых на уроке:

1) электромагнитные колебания, колебательный контур;

2) универсальность основных закономерностей колебательных процессов для колебаний любой физической природы;

3) гармонические колебания;

4) физический смысл характеристик колебаний.

5) графики зависимости электрического заряда, силы тока и напряжения от времени при свободных электромагнитных колебаниях.

6) определение по графику характеристик колебаний;

7) аналогия между механическими и электромагнитными колебаниями.

Электромагнитными колебаниями называют периодические изменения со временем заряда, силы тока и напряжения.

Свободными колебаниями называют колебания, возникающие в колебательной системе за счет первоначально сообщенной этой системе энергии.

Система, состоящая из конденсатора и катушки индуктивности, присоединенной к его обкладкам, называется колебательным контуром.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частота колебаний – число колебаний в единицу времени.

Основная и дополнительная литература по теме урока:

Основное содержание урока

Колебательным контуром называется система, состоящая из конденсатора и катушки, присоединенной к его обкладкам, в которой могут происходить свободные электромагнитные колебания

Электромагнитные колебания в контуре происходят с большой частотой и определять его характеристики без осциллографа невозможно.

Развертка получаемая на экране осциллографа схожа с той, что вычерчивает маятник с песочницей над движущимся листом бумаги при колебаниях математического маятника.

Чтобы в колебательном контуре возникли колебания, необходимо сообщить колебательному контуру энергию, зарядив конденсатор от источника тока.

Энергия, полученная конденсатором заключена в электрическом поле обкладок

где — заряд конденсатора, C – его электроемкость.

Между обкладками конденсатора возникает разность потенциалов .

При разрядке конденсатора энергия электрического поля превращается в энергию магнитного поля, определяемая по формуле

где – индуктивность катушки, – сила переменного тока.

Полная энергия колебательного контура равна

Когда конденсатор разрядится полностью, вся энергия электрического поля превращается в энергию магнитного поля. Когда сила тока и созданное им магнитное поле начинает уменьшаться, возникает ЭДС самоиндукции, стремящийся поддержать ток, и начинается перезарядка конденсатора. При свободных колебаниях через промежутки времени, равные периоду колебаний, состояние системы в точности повторяется. Полная энергия такой системы любой момент времени равно максимальной энергии электрического поля или максимальной энергии магнитного поля.

Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями. Характер периодического изменения различных величин одинаков. При механических колебаниях периодически изменяются координата тела x и проекция его скорости , а при электромагнитных колебаниях изменяются заряд q конденсатора и сила тока i в цепи.

Индуктивность катушки L аналогична массе тела m, при колебаниях груза на пружине, кинетическая энергия тела , аналогична энергии магнитного поля тока .

Роль потенциальной энергии выполняет энергия заряда конденсатора:

Координата тела аналогична заряду конденсатора.

Полная энергия колебательного контура, в любой момент времени, равна сумме энергий магнитного и электрического полей:

Производная полной энергии по времени равна нулю при R = 0. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

Электрический заряд и сила тока, при свободных колебаниях с течением времени изменяются по закону синуса или косинуса, то есть совершают гармонические колебания.

Циклическая частота для свободных электрических колебаний:

Период свободных колебаний в контуре равен:

Период свободных электрических колебаний в колебательном контуре зависит от индуктивности катушки и емкости конденсатора.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частотой колебаний называется величина, обратная периоду колебаний:

Частоту свободных колебаний называют собственной частотой колебательной системы.

Заряд конденсатора изменяется по гармоническому закону:

где – амплитуда колебаний заряда. Сила тока также совершает гармонические колебания:

где – амплитуда колебаний силы тока. Колебания силы тока опережают по фазе колебания заряда на .

Разбор типовых тренировочных заданий

Задача 1. Идеальный колебательный контур состоит из конденсатора ёмкостью 2 мкФ и катушки индуктивности. В контуре происходят свободные электромагнитные колебания. В таблице приведена зависимость энергии W, запасённой в конденсаторе идеального колебательного контура, от времени t.

Источник

Колебательный контур. Превращение энергии при электромагнитных колебаниях

Урок 12. Физика 11 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Колебательный контур. Превращение энергии при электромагнитных колебаниях»

«Радость видеть и понимать —

есть самый прекрасный дар природы»

В данной теме разговор пойдёт о простейшем колебательном контуре и о превращениях энергии, которые происходят при электромагнитных колебаниях.

Электромагнитными колебаниями называют периодические изменения со временем электрических и магнитных величин в электрической цепи. Они бывают двух видов — свободные и вынужденные.

Под свободными колебаниями понимают колебания, возникающие в системе за счет расходования сообщенной этой системе энергии, которая в дальнейшем не пополняется.

Вынужденные электромагнитные колебания — это периодические изменения силы тока и других электрических величин в цепи под действием переменной электродвижущей силы от внешнего источника.

Рассмотрим более подробно процесс становления свободных электромагнитных колебаний в системе.

Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединенной к его обкладкам. Такая система называется колебательным контуром. Но мало иметь только катушку и конденсатор, для того, чтобы в колебательном контуре возникли свободные электромагнитные колебания, необходимо этому контуру сообщить энергию — зарядить конденсатор.

Из представленной схемы видно, как можно зарядить конденсатор? Когда переводится ключ в положение 1, то конденсатор начинает заряжаться от источника тока.

Когда ключ переводится в состояние 2, то конденсатор начинает разряжаться, и почему-то при этом в контуре начинают возникать колебания силы тока, заряда, напряжения.

Для того чтобы выяснить почему это возникает, рассмотрим процессы, происходящие в колебательном контуре в различные моменты времени: в момент времени t = 0, через четверть периода t = T/4, через половину периода t = T/2, через три четвертых периода t = 3T/4 и, момент времени, равный периоду t = T.

В момент времени t = 0, конденсатор заряжен от источника тока. При этом верхняя его пластина заряжена положительно, а нижняя отрицательно. Получается, что заряд верхней пластины равен + q_max, напряжение между обкладками конденсатора — U_max и, так как еще не началась разрядка конденсатора, сила тока в цепи равна нулю

Маленькими буквами q, u и i обозначены мгновенные значения заряда, напряжения и силы тока.

Так как еще отсутствует ток в цепи, то отсутствует и магнитное поле. Поэтому вся энергия колебательного контура будет заключена в электрическом поле конденсатора. Эта ситуация эквивалентна ситуации с механическими колебаниями груза на нити и соответствует тому положения, когда груз вывели из положения равновесия, тем самым сообщив ему потенциальную энергию.

В промежутке от начала отсчета времени до момента времени, равного четверти периода t = T/4, происходит разрядка конденсатора. При этом, разряжаясь, конденсатор создает в контуре ток, идущий по часовой стрелке. Однако, благодаря тому, что в контуре есть катушка, обладающая индуктивностью, в контуре возникает переменное магнитное поле. А это поле создает ток самоиндукции, который будет направлен против тока в контуре и не позволяет току в контуре мгновенно достичь максимального значения. Поэтому конденсатор разряжается не мгновенно, а через некоторый промежуток времени. При этом будет увеличиваться и индукция магнитного поля, т.е. будет возрастать энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора будет превращаться в энергию магнитного поля катушки.

К моменту времени, равным четверти периода t = T/4, конденсатор полностью разрядится, напряжение между его обкладками станет равным нулю, и электрическое поле в нем будет отсутствовать. К этому времени ток в контуре, и индукция магнитного поля этого тока достигают максимальных значений. Значит, вся энергия контура в этот момент заключена в его магнитном поле.

Эта ситуация эквивалентна ситуации с механическими колебаниями груза на нити, в момент прохождения груза положения равновесия, когда его потенциальная энергия полностью переходит в кинетическую.

В следующий промежуток времени, от одной четвертой периода до полупериода, происходит уменьшение тока в катушке. При этом в ней возникает ЭДС самоиндукции и индукционный ток такого направления, что он препятствует уменьшению разрядного тока, т.е. совпадает с его направлением. Конденсатор начинает перезаряжаться — его нижняя обкладка получает избыточный положительный заряд, а верхняя — отрицательный, и между обкладками конденсатора появляется электрическое поле. В указанном интервале времени сила тока и индукция магнитного поля начинают уменьшаться, а напряженность электрического поля и напряжение между обкладками конденсатора возрастают. Значит, происходит превращение энергии магнитного поля катушки в энергию электрического поля конденсатора.

К моменту времени, равным полупериоду t = T/2, ток в контуре полностью прекращается. При этом полностью исчезает и магнитное поле. А напряженность электрического поля и напряжение между обкладками конденсатора достигают своего максимального значения. Таким образом, вся энергия колебательного контура теперь заключена в его электрическом поле.

Эта ситуация эквивалентна ситуации с механическими колебаниями груза на нити, в момент отклонения груза от положения равновесия в противоположную сторону, когда его кинетическая энергия полностью переходит в потенциальную.

В промежуток времени от полупериода до трех четвертых периода конденсатор вновь разряжается и, тем самым, вновь создает ток в контуре. Однако теперь положительно заряжена нижняя обкладка конденсатора, поэтому направление тока в контуре меняется на противоположное. Значит, меняется и направление индукции создаваемого им магнитного поля.

Этот ток не может достигнуть своего максимального значения сразу, так как в катушке опять возникает ЭДС самоиндукции, которая и препятствует быстрому нарастанию тока. В указанном промежутке времени сила тока и индукция магнитного поля этого тока увеличиваются, а напряженность электрического поля и напряжение между обкладками конденсатора уменьшаются. Опять происходит переход электрической энергии в магнитную.

К моменту времени, равным три четвертых периода t = 3T/4, конденсатор полностью разрядится. Напряжение между его обкладками падает до нуля, а электрическое поле полностью исчезает. В это время ток в контуре и индукция магнитного поля достигают своего максимального значения. А значит, вся электрическая энергия превратилась в энергию магнитного поля, аналогично тому, как груз на нити, возвращаясь, вновь проходит положение своего равновесия и его потенциальная энергия полностью переходит в кинетическую.

К моменту времени, равному полному периоду t = T, ток в контуре полностью прекращается и исчезает магнитное поле. А напряженность электрического поля конденсатора и напряжение на его обкладках вновь становятся максимальными. Теперь опять вся энергия колебательного контура заключена в его электрическом поле, вторая перезарядка возвращает контур в исходное состояние. Эта ситуация аналогично тому, как груз на нити возвращается в свое исходное положение, а его кинетическая энергия полностью переходит в потенциальную.

Таким образом, завершилось полное колебание и в дальнейшем процесс повторяется в уже рассмотренном нами порядке.

Если бы не было потерь энергии, то этот бы процесс продолжался бы сколь угодно долго и колебания были бы незатухающими. Через промежутки времени, равные периоду колебаний, состояние системы в точности повторялось бы. При этом полная энергия такой системы сохранялась бы неизменной, а ее значение в любой момент времени было бы равно максимальной энергии электрического поля или максимальной энергии магнитного поля.

На данном примере был рассмотрен идеальный колебательный контур или, как его еще называют, контур Томсона, но в действительности потери энергии неизбежны. Так, в частности, катушка, как и соединительные провода, обладает сопротивлением, а это непосредственно ведет к тому, что энергия электромагнитного поля постепенно превращается во внутреннюю энергию проводника. Вследствие чего колебания в цепи со временем прекращаются.

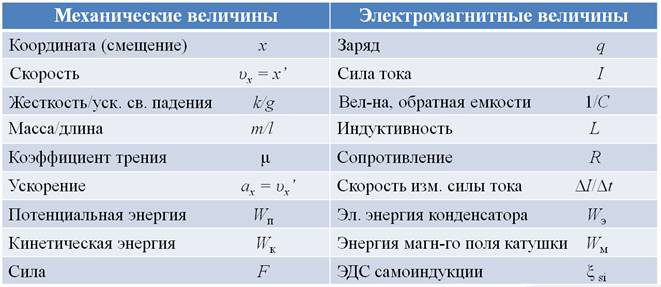
Входе рассмотрения процессов, происходящих в колебательном контуре, постоянно сравнивались эти процессы с колебаниями математического или нитяного маятника. Как оказывается, эти процессы описываются одинаковыми уравнениями, что позволяет переносить закономерности, полученные при изучении одного вида колебаний, на колебания другой природы.

Для наглядности, в одной таблице, представлены соответствия между электромагнитными и механическими величинами.

– Идеальный колебательный контур — это цепь, состоящая из последовательно соединенных катушки индуктивностью L и конденсатора емкостью C.

– В таком колебательном контуре энергия электрического поля заряженного конденсатора периодически переходит в энергию магнитного поля тока. И, если отсутствует сопротивление в контуре, полная энергия электромагнитного поля остается неизменной.

Источник

Колебательный контур

Рис. 1. Колебательный контур

В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток ( ). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).

Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.

При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).

Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.

Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:

Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:

Для идеального контура полная энергия системы остаётся постоянной:

Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:

Вывод: работа с контурами достаточно сложна. Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.

Источник

Колебательный контур

Разделы: Физика

Постановка задачи: Мы уже много знаем о механических колебаниях: свободные и вынужденные колебания, автоколебания, резонанс и т.д. Приступаем к изучению электрических колебаний. Тема сегодняшнего урока: получение свободных электромагнитных колебаний.

Вспомним вначале: Каким условиям должна соответствовать колебательная система, система, в которой могут возникать свободные колебания. Ответ: в колебательной системе должна возникать возвращающая сила и происходить превращение энергии из одного вида в другой.

(Разбор нового материала по презентации с подробным пояснением всех процессов и записью в тетради первых двух четвертей периода, 3 и 4-ые четверти описать дома, по образцу).

Колебательный контур – это электрическая цепь, в которой можно получить свободные электромагнитные колебания. К.К. состоит всего из двух приборов: катушки индуктивностью L и конденсатора электроёмкостью С. Идеальный колебательный контур не имеет сопротивления.

Чтобы сообщить энергию в К.К., т.е. вывести его из положения равновесия, нужно временно разомкнуть его цепь и поставить ключ с двумя положениями. Когда ключ замкнут на источник тока, то конденсатор заряжается до максимального заряда. Этим подают в К.К. энергию в виде энергии электрического поля. Когда ключ замкнут в правое положение, то источник тока отключен, К.К. предоставлен самому себе.

Такое состояние К.К. соответствует положению математического маятника в крайнем правом положении, когда его вывели из состояния покоя. Колебательный контур выведен из положения равновесия Заряд конденсатора – максимален и энергия заряженного конденсатора – энергия электрического поля максимальна. Будем рассматривать весь процесс, который происходит в нём по четвертям периода.

В 3-ей четверти периода происходит всё также, что и в 1-ой четверти, только противоположного направления. Конденсатор начинает разряжаться. Ток разрядки растёт постепенно, в течение всей четверти, т.к. быстрому росту его препятствует явление самоиндукции. Ток растёт до максимальной величины, пока конденсатор не разрядится. К концу 3-ей четверти энергия электрического поля превратится в энергию магнитного поля, полностью, если не будет утечки. Это соответствует такому положению маятника, когда он снова проходит положение равновесия, но в противоположном направлении.

В 4-ой четверти периода происходит всё так же, как и во 2-ой четверти, только в противоположном направлении. Ток, поддерживаемый магнитным полем, постепенно убывает, поддерживаемый ЭДС самоиндукции и перезаряжает конденсатор, т.е. возвращает его к первоначальному положению. Энергия магнитного поля превращается в энергию электрического поля. Что соответствует возвращению математического маятника в первоначальное положение.

Анализ рассмотренного материала:

1. Можно ли колебательный контур рассматривать, как колебательную систему? Ответ: 1. В колебательном контуре происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. 2. Явление самоиндукции играет роль возвращающей силы. Поэтому колебательный контур рассматривать, как колебательную систему. 3. Колебания в К.К. можно считать свободными.

2. Можно ли колебания в К.К. рассматривать, как гармонические? Анализируем изменение величины и знака заряда на обкладках конденсатора и мгновенного значения тока и его направления в цепи.

3. Что в колебательном контуре колеблется? Какие физические тела совершают колебательные движения? Ответ: колеблются электроны, они совершают свободные колебания.

4. Какие физические величины изменяются при работе колебательного контура? Ответ: изменяются сила тока в цепи, заряд в конденсаторе, напряжение на обкладках конденсатора, энергия электрического поля и энергия магнитного поля.

5. Период колебаний в колебательном контуре зависит только от индуктивности катушки L и ёмкости конденсатора C. Формула Томсона: Т = 2π можно сравнить и с формулами для механических колебаний.

Источник