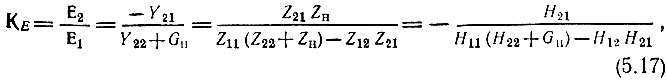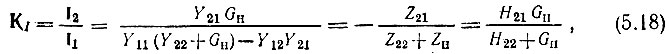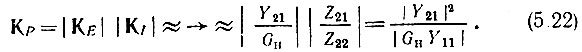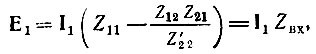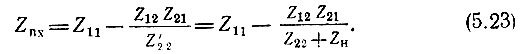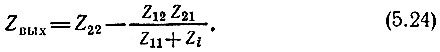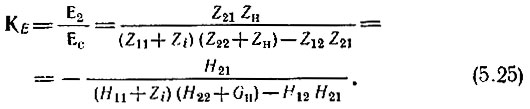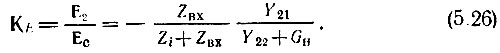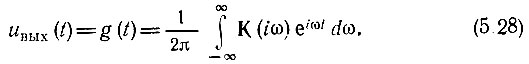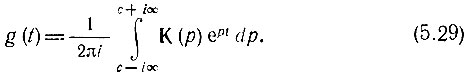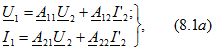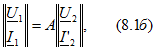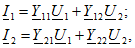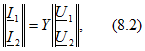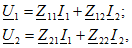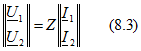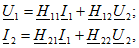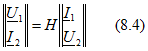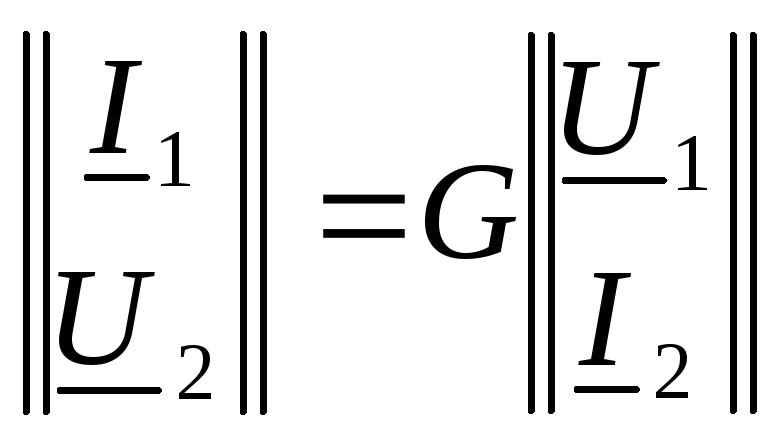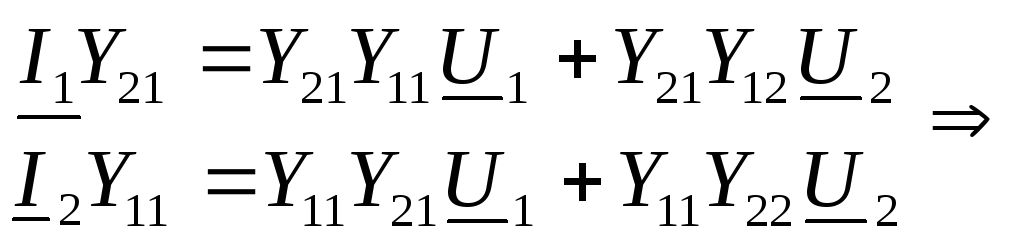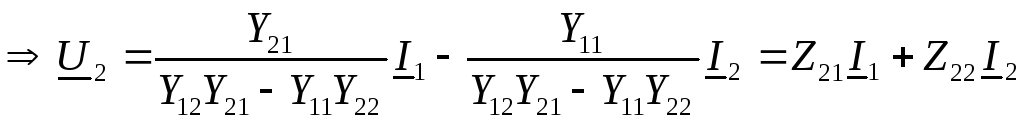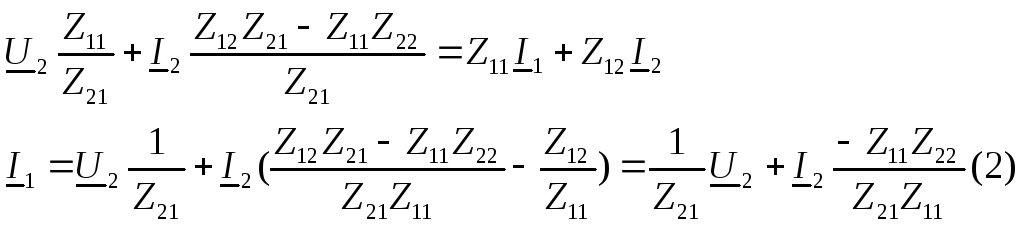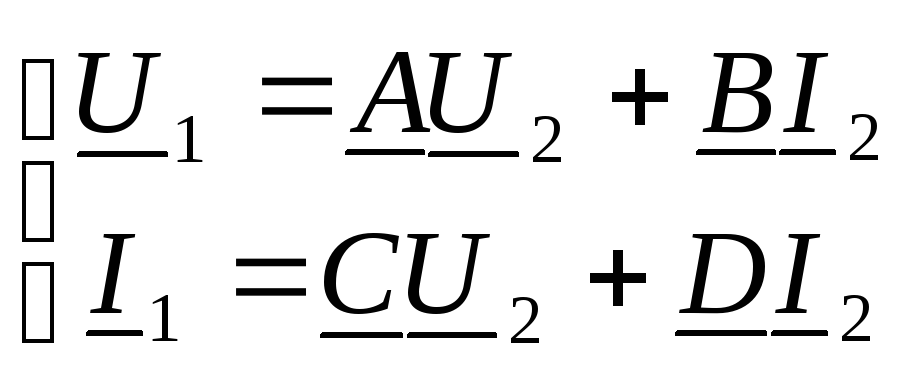в каком случае четырехполюсник является активным

В каком случае четырехполюсник является активным

5.3. Активный четырехполюсник как линейный усилитель

Приведенные в предыдущем параграфе выражения (5.13)-(5.16), записанные в форме

можно рассматривать как коэффициенты усиления соответственно по напряжению и по току в активном четырехполюснике.

В широкополосных усилителях, как правило, усилительные приборы (транзисторы, лампы и др.) обеспечивают (при правильном выборе нагрузки) выполнение следующих неравенств:

Поэтому при грубой оценке усилительной способности четырехполюсника можно исходить из приближенных равенств

Отсюда следует, что коэффициент усиления по мощности (выраженной в вольтамперах)

Из (5.22) очевидна решающая роль параметра Y₂₁ (соответственно Z₂₁ и H₂₁) в усилении мощности колебания в активном четырехполюснике. Физический смысл этого параметра раскрывается в следующих параграфах на примерах некоторых усилительных приборов.

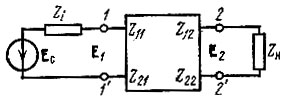
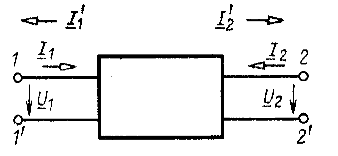
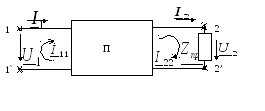
При анализе активного четырехполюсника как усилителя важное значение имеют такие его параметры, как входное и выходное сопротивления. На рис. 5.6 представлена обобщенная схема, содержащая источник сигнала Е_с, активный четырехполюсник и сопротивление нагрузки Z_H.

Рис. 5.6. Обобщенная схема активного четырехполюсника с учетом параметров источника сигнала и нагрузки

Входное сопротивление (между зажимами 1-1′) легко определить с помощью уравнений (5.4) в сочетании с (5.14).

Подставив Ι₂ из (5.14) в первое уравнение (5.4), получим

Под выходным сопротивлением четырехполюсника подразумевается сопротивление между зажимами 2-2′ при Ε_c = 0 (но с учетом внутреннего сопротивления источника сигнала Z_i). Сопротивление Z_i рассматривается при этом как нагрузка.

По аналогии с (5.23) при замене Z₁₁ на Z₂₂ и Z_H на Z_i получаем

При учете внутреннего сопротивления Z_i источника сигнала под коэффициентом усиления следует подразумевать отношение Ε₂/Ε_c = Κ_E. Этот коэффициент можно найти с помощью соответствующих формул (5.17), (5.18) добавлением Z_i к Z₁₁ или Н₁₁. Таким образом,

При использовании Y-матрицы нетрудно получить выражение

Это выражение совпадает с обычным определением передаточной функции линейного четырехполюсника.

Из приведенных общих соотношений видно, что структура передаточной функции активного четырехполюсника и характер частотной зависимости этой функции определяются частотными свойствами параметров Z или Y. В этом отношении между линейными активным и пассивным четырехполюсниками нет никакого различия. Задание Z(ω) и Y(ω) однозначно определяет и временные характеристики линейной активной цепи: импульсную характеристику и переходную функцию.

Определяемая формулами (5.17), (5.18) безразмерная, в общем случае комплексная функция является важнейшей характеристикой четырехполюсника. Она определяется в стационарном режиме при гармоническом возбуждении четырехполюсника.

Передаточную функцию часто удобно представлять в форме

Модуль К(ω) иногда называют амплитудно-частотной или просто частотной характеристикой четырехполюсника. Аргумент φ(ω) коэффициента передачи называют фазочастотной (или просто фазовой) характеристикой четырехполюсника.

Для активных линейных цепей, как и для пассивных, под импульсной характеристикой цепи g(t) подразумевается отклик, реакция цепи на воздействие, имеющее вид единичного импульса (дельта-функции). Связь между g(t) и К(iω) нетрудно установить с помощью интеграла Фурье.

Если на входе четырехполюсника действует единичный импульс э. д. с., обладающий спектральной плотностью, равной единице для всех частот, то спектральная плотность выходного напряжения равна просто К(iω). Следовательно, отклик на единичный импульс, т. е. импульсная характеристика цепи, легко определяется с помощью обратного преобразования Фурье [см. (2.49)], примененного к передаточной функции К(ω):

В дальнейшем импульсную характеристику будем обозначать функцией g(t), под которой можно подразумевать не только напряжение, но и любую другую электрическую величину, являющуюся откликом на воздействие в виде дельта-функции.

Если передаточная функция задана в виде функции Κ(р), т. е. в виде преобразования Лапласа от функции g(t), то выражение (5.28) можно записать * в форме обратного преобразования Лапласа

* ( Здесь и в дальнейшем обозначения передаточной функции цепи, рассматриваемой как преобразование Фурье или Лапласа от импульсной характеристики g(t), будут различаться только аргументом: К(iω) или К(р) (см. § 2.13).)

Переходная функция цепи h(t) представляет собой отклик, реакцию цепи на воздействие, имеющее вид «единичного скачка». Так как такое воздействие является интегралом от единичного импульса (т. е. дельта-функции), то и между h(t) и g(t) существует интегральное соотношение

В последующих главах при анализе передачи сигналов через радиоцепи чаще всего будет применяться импульсная характеристика g(t).

Источник

Активные и пассивные четырехполюсники. Формы записи уравнений четырехполюсников. Схемы замещения. Связь между входными и выходными параметрами.

Четырехполюсники бывают активными(с источниками ЭДС внут­ри) и пассивными.

В схеме пассивного четырехполюсника могут быть ЭДС, но они должны взаимно компенсироваться.

К активным четырехполюсникам относятся различные усилители, схемы, содержащие источники энергии, и т. п. Пассивными четырехпо­люсниками являются трансформаторы, линии электропередач, фильт­ры и др.

На схеме замещения четырехполюсник обозначается прямоугольни­ком. Активный четырехполюсник обозначается буквой А.

Симметричный четырехполюсник – четырехполюсник, у которого схема одинакова относительно его входных и выходных зажимов. Тогда для симметричного четырехполюсника Z11 = Z22. Еще: если при перемене местами источника и приемника энергии их токи не меняются, то такой четырехполюсник называется симметричным.

Параметры Z, Y, H и A характеризуют связи между входными и выходными токами и напряжениям четырехполюсника.

Параметры Z, Y и H с индексами 11 называются входными сопротивлениями или проводимостями, с индексами 22 — выходными величинами. Они определяются в режиме холостого хода или короткого замыкания на противоположной стороне четырехполюсника в зависимости от того, какая пара переменных выступает в правой части данной системы. Так, H₁₁ — входное сопротивление в режиме короткого замыкания, а Z₁₁ — входное сопротивление при холостом ходе на выходе. Выходная проводимость H₂₂ определяется при холостом ходе, а Y₂₂ — при коротком замыкании на входе. Параметры с индексами 21 называются передаточными от входа к выходу. Безразмерный параметр Н₂₁ определяет усиление тока четырехполюсником в режиме короткого замыкания на выходе. Параметры с индексами 12 характеризуют передачу сигналов с выхода на вход. A-параметры с одинаковыми индексами 11 и 22 безразмерные. Они определяются отношением напряжений на входе и выходе в режиме холостого хода и токов в режиме короткого замыкания. Параметр A₁₂ имеет размерность сопротивления, A₂₁ — проводимости.

А-форма	; ;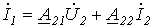
Y-форма	; ;	; ; ; ;
Z-форма	; ;	; ; ; ;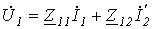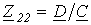
Н-форма	; ;	; ; ; ;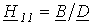
G-форма	; ;	; ; ; ;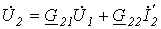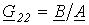
B-форма	; .	; ; ; .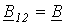

Дата добавления: 2015-04-16 ; просмотров: 46 ; Нарушение авторских прав

Источник

3. Четырехполюсники

Четырехполюсником называют сколь угодно сложную электрическую цепь, имеющую четыре внешних зажима, через которые она может взаимодействовать с внешними цепями. Трансформатор, фильтр, линию электропередачи, мостовую схему и т.д. можно рассматривать как четырехполюсник.

Теория четырехполюсников позволяет устанавливать связи между напряжениями, токами двух ветвей, подключенных к четырем зажимам сколь угодно сложной цепи, без исследования режимов работы ее отдельных участков.

Суть теории заключается в следующем:

Пользуясь некоторыми обобщенными параметрами четырехполюсника, можно определять напряжения и токи на его входе и выходе, не рассматривая процессы, происходящие внутри четырехполюсника.

Сложная электрическая цепь может быть рассмотрена как совокупность объединенных по определенной схеме простейших четырехполюсников. Теория четырехполюсников позволяет рассчитать параметры такого составного четырехполюсника при помощи параметров входящих в него четырехполюсников.

Получаемые таким образом значения электрических величин на входе и выходе позволяют оценить режим работы канала передачи в целом. При этом обобщенные параметры четырехполюсника позволяют сопоставить и правильно оценить передающие свойства электрических цепей, различных по своим свойствам и структуре.

Теория четырехполюсников позволяет находить структуру и элементы четырехполюсника по заданным характеристикам, т.е. решать задачу синтеза.

3.1. Классификация четырехполюсников

Четырехполюсники классифицируются по разным признакам. Они могут быть активными и пассивными, симметричными и несимметричными, линейными и нелинейными, обратимыми и необратимыми, эквивалентными и неэквивалентными.

Активные четырехполюсники – это четырехполюсники, которые содержат ветви с нескомпенсированными источниками энергии, при этом напряжение на разомкнутых зажимах не равно нулю. Пассивные четырехполюсники либо не содержат источников энергии, либо, если они есть, то суммарное их действие взаимно компенсируется внутри четырехполюсника таким образом, что напряжение на входных и выходных зажимах равно нулю. В дальнейшем рассматривается теория пассивных четырехполюсников, т.к. активный четырехполюсник может быть заменен эквивалентным ему пассивным и вынесенным за зажимы последнего эквивалентными источниками ЭДС.

Если четырехполюсник симметричный, то перемена мест подключения входных и выходных зажимов не изменит токораспределения во внешней цепи.

В линейных четырехполюсниках связь между токами и напряжениями имеет линейную зависимость. В таких четырехполюсниках нелинейные элементы (вольт-амперные характеристики их имеют нелинейный характер) отсутствуют.

Обратимые четырехполюсники – это такие четырехполюсники, для которых справедлив принцип взаимности (отношение напряжения на входе к току на выходе не зависит от того, какая пара зажимов выбрана в качестве входных).

Эквивалентные четырехполюсники – это такие четырехполюсники, при взаимной замене которых входные и выходные токи и напряжения не изменятся. Четырехполюсники также подразделяются по схемам соединения входящих в них элементов: Т, П, Г-образные, мостовые и др.

Источник

Четырехполюсники и многополюсники

Ранее были рассмотрены общие методы расчета линейных электрических цепей, например методы наложения, контурных токов, узловых потенциалов. Применив эти методы, можно найти режим работы любой линейной цепи.

В различных областях электротехники особенно часто применяются аппараты и устройства с двумя парами выводов, при помощи которых они соединяются с другими участками электрической цепи, т. е. четырехполюсники.

На практике четырехполюсники и цепи, которые целесообразно представить состоящими из нескольких четырехполюсников, применяются прежде всего для передачи и преобразования электрических сигналов, несущих информацию. Тракт передачи информации, или канал связи, как правило, состоит из ряда четырехполюсников, включенных между генератором (передатчиком) сигналов и приемником сигналов. B тракт передачи обычно входят:

К четырехполюсникам относятся также некоторые цепи обратной связи электронных генераторов и усилителей, участки линий передачи электрической (электромагнитной) энергии, цепи регулирования различных параметров машин (скорости, давления, напряжения) и т. д.

Таким образом, теория четырехполюсников дает возможность единым методом анализировать системы, самые различные по структуре и принципу действия. Кроме того, сложная цепь расчленяется на более простые части, характеристики которых дают полное представление о режиме работы всей цепи.

Рис. 8.1

Будем считать, что источники питания, приемники, двухполюсники, четырехполюсники и вообще любые участки цепи с парными выводами могут присоединяться только к выводам четырехполюсника, которые обозначены одинаковыми цифрами. Такие четырехполюсники называют проходными.

Все четырехполюсники подразделяются еще на две группы: пассивные и активные. В пассивных четырехполюсниках нет зависимых или независимых источников напряжения (ЭДС) или тока, активные четырехполюсники содержат зависимые или независимые источники. Пассивными четырехполюсниками являются, например, линии передачи сигналов, трансформаторы, аттенюаторы, корректирующие контуры. К активным относятся усилители, собранные на транзисторах или электронных лампах, в том числе операционные усилители, лампы бегущей волны и др.

Далее предполагается, что напряжения и токи источников питания, которые могут подключаться к выводам 1-1′ и 2-2′, а значит, и напряжения, и токи на всех участках цепи синусоидальные.

На практике устройства, которые анализируются как четырехполюсники, чаще работают в цепях несинусоидального тока, хотя могут быть и в цепях синусоидального, и в цепях постоянного токов. Для применения рассматриваемой здесь теории к цепям несинусоидального тока необходимо исследовать частотные зависимости параметров четырехполюсников. Все расчетные формулы и соотношения могут быть отнесены и к цепям постоянного тока, если положить частоту равной нулю.

Для исследования четырехполюсников необходимо прежде всего установить зависимости между четырьмя величинами, определяющими режим его работы: напряжениями и токами на первичных и вторичных выводах.

Рассмотрим сначала режимы работы неавтономных активных и пассивных проходных четырехполюсников.

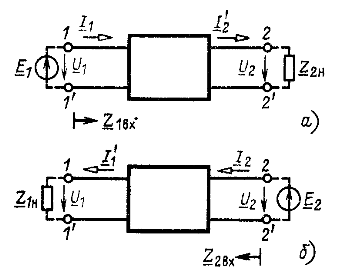
Зависимости между двумя напряжениями и двумя токами, определяющими режим на первичных и вторичных выводах, могут быть записаны в различной форме. Если считать две из указанных величин заданными, то две другие величины будут связаны с ними системой двух уравнений, которые называются уравнениями четырехполюсника.

Рис. 8.2

или в матричной форме

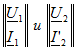
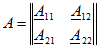
где — матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах;

— квадратная матрица коэффициентов.

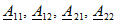
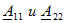
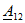
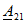
В этих уравнениях коэффициенты определяют сам четырехполюсник и зависят от схемы соединения и параметров составляющего четырехполюсник элементов электрической цепи; — безразмерные коэффициенты; имеет размерность сопротивления, а — проводимости.

Всего можно записать шесть различных по форме, но по существу эквивалентных, т. е. математически равносильных, пар уравнений (число сочетаний из четырех по два).

с коэффициентами, размерность которых, как и в первых трех системах уравнений, непосредственно следует из самой записи уравнений.

Источник

po_temam / Четырехполюсники

Общая теория четырехполюсников.

Четырехполюсником называют часть электрической цепи, имеющей две пары зажимов, которые могут быть входными или выходными. К входным зажимам присоединяют источник питания, а к выходным зажимам – приемники энергии.

Теория четырехполюсников дает возможность единым методом анализировать электрические схемы большого объема.

Пассивный четырехполюсник – не содержащий источников энергии (ЛЭП, усилители).

Активный четырехполюсник – содержащий источники энергии.

Автономный четырехполюсник – у которого действие внутренних независимых источников энергии не компенсируется.

Линейные и нелинейные четырехполюсники.

Четырехполюсник является нелинейным, если в четырехполюснике имеется хотя бы один нелинейный элемент.

Симметричный и несимметричный четырехполюсник.

Симметричный четырехполюсник – это четырехполюсник, в котором перемена местами его входных и выходных зажимов не изменяет его входных и выходных токов и напряжений.

Уравнение линейного, пассивного четырехполюсника.

или в матричной форме

=А,

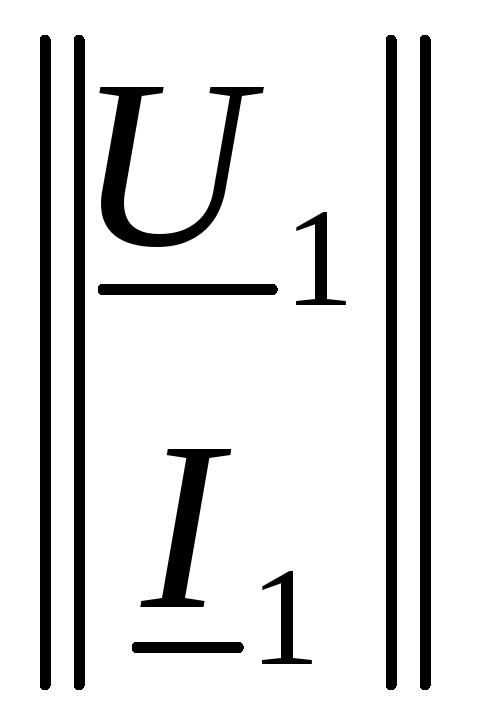
где и — матрицы-столбцы напряжения и тока на первичных и вторичных выводах соответственно

А=— квадратная матрица коэффициентов.

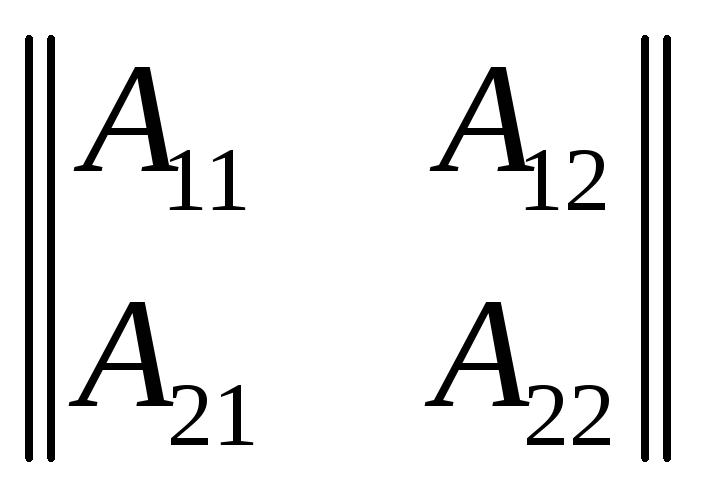
Всего можно записать 6 различных по форме, но по существу эквивалентных пар уравнений.

Y = или

=

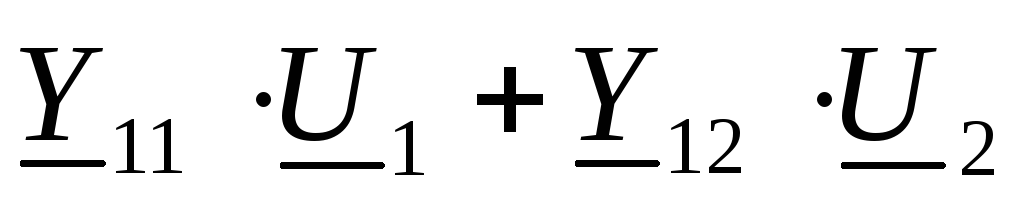
Z или

H или

G или

B или

Эквивалентные четырехполюсники – четырехполюсники у которых при взаимной замене входные и выходные токи и напряжения не изменяются.

Линейный, пассивный четырехполюсник в установившемся синусоидальном режиме.

∆₁₁/∆; ∆=; ∆₁₁=;

∆₁₁/∆-∆₁₂/∆; =∆₂₁/∆-∆₂₂/∆;

;

; Z₁₂=-Z₂₁;Y₁₂=-Y₂₁ ;

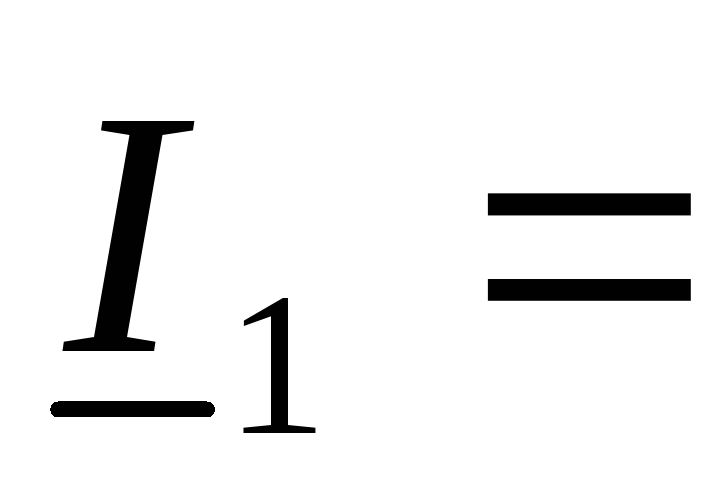
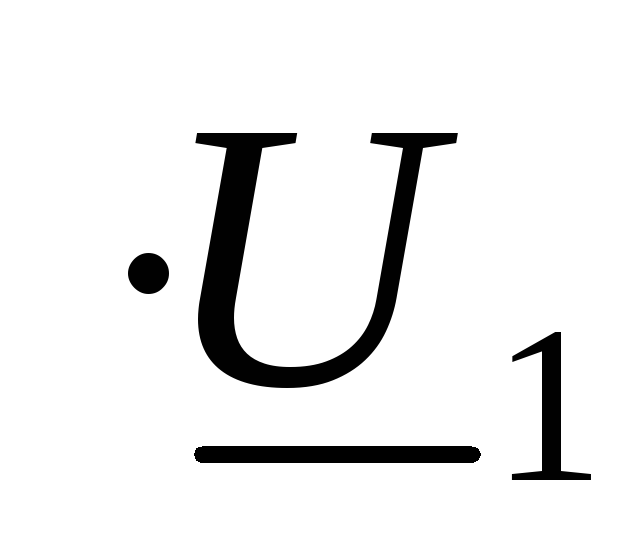
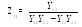
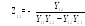
Перейдем к системе А параметров

Подставляем полученный результат в (*):

Используя выражения (1) и (2) запишем систему:

,где

Таким образом, пассивный четырехполюсник характеризуется тремя независимыми параметрами, а четвертый определяется из этих независимых.

Экспериментальное определение параметров четырехполюсников.

Измерение параметров при Z_пр=∞ I₂=0 – опыт холостого хода(ХХ)

Измерение параметров при Z_пр=0 U₂=0 – опыт короткого замыкания(КЗ)

Особо важно при измерении параметров мощных устройств, так как мощность в опытах ХХ и КЗ меньше, чем в номинальном режиме.

Тогда для опыта холостого хода имеем:

И для опыта короткого замыкания:

Из полученных выражений можно найти :

Эквивалентные схемы четырехполюсников.

Источник