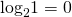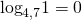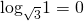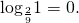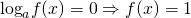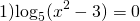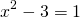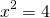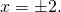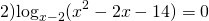в каком случае логарифм равен 0

Логарифм равен 0

Когда логарифм равен 0?

Каким бы ни было основание логарифма, логарифм равен нулю в единственном случае — когда под знаком логарифма стоит единица.

Если логарифм, под знаком которого стоит выражение с переменной, равен 0, то это выражение может быть равным только единице:

При этом дополнительно накладывать условие на выражение под знаком логарифма не нужно — поскольку оно равно единице, то оно автоматически больше нуля.

Если основание a — число, то область допустимых значений: x — любое число (x∈R).

Если a=a(x), то ОДЗ: a(x)>0, a(x)≠1.

Так как логарифм равен нулю, выражение, стоящее под знаком логарифма, равно единице:

Источник

Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log₆ 4 + log₆ 9 = log₆ (4 · 9) = log₆ 36 = 2.

Основания одинаковые, используем формулу разности:
log₂ 48 − log₂ 3 = log₂ (48 : 3) = log₂ 16 = 4.

Задача. Найдите значение выражения: log₃ 135 − log₃ 5.

Снова основания одинаковые, поэтому имеем:
log₃ 135 − log₃ 5 = log₃ (135 : 5) = log₃ 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Избавимся от степени в аргументе по первой формуле:
log₇ 49 6 = 6 · log₇ 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

[Подпись к рисунку]

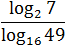
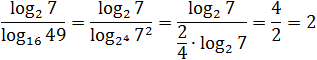
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log₂ 7. Поскольку log₂ 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

[Подпись к рисунку]

[Подпись к рисунку]

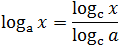
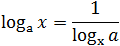
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log₅ 16 · log₂ 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log₅ 16 = log₅ 2 4 = 4log₅ 2; log₂ 25 = log₂ 5 2 = 2log₂ 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

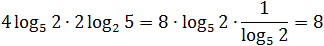
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log₉ 100 · lg 3.

Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

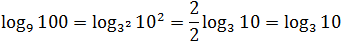
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

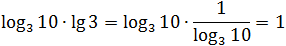
Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

Задача. Найдите значение выражения:

[Подпись к рисунку]

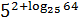
Заметим, что log₂₅ 64 = log₅ 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

[Подпись к рисунку]

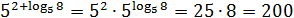
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Источник

Логарифмы и их свойства

Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.

Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:

Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.

Теперь при помощи этой таблицы введем понятие логарифма.

Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:

Аналогично, глядя в таблицу получим, что:

Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.

Теперь дадим определение логарифма в общем виде:

Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)

Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:

Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:

Или логарифм шести по основанию 4:

На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!

Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:

Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:

Как посчитать логарифм

Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).

При этих ограничениях логарифм существует.

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.

Теперь давайте разберем общий алгоритм вычисления логарифмов:

Давайте разберем на примерах.

Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)

Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)

Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)

Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)

Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)

Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.

\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.

Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.

Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.

Десятичный логарифм

Натуральный логарифм

Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.

У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.

Свойства логарифмов

Давайте разберем несколько примеров на свойства логарифмов.

Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.

Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.

Пример 10. Формула \(5,6\). Свойства степени.

Логично, что будет выполняться и такое соотношение:

Пример 11. Формулы \(7,8\). Переход к другому основанию.

Источник

Логарифмы

Определение логарифма

Понятие логарифма и основного логарифмичесгого тождества

Понятие логарифма и основного логарифмическое тождества состоят в тесной зависимости, т.к. определение логарифма в математической записи и является основным логарифмическим тождеством.

Основное логарифмическое тождество вытекает из определения логарифма:

Логарифмом называют показатель степени n, при возведении в которую числа а получают число b.

Показательное уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и имеет единственный корень при положительном b. Этот корень называется логарифмом числа b по основанию а и записывают:

Основное логарифмическое тождество

4 log₂ 7 =2 2 log₂ 7 = (2 log₂ 7 ) 2 = 7 2 = 49

2 1 + log₂ 7 = 2 · 2 log₂ 7 = 2 · 7 = 14

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X. и преобразовываем в и преобразовываем в Запомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Два очевидных следствия определения логарифма

log a 1 = 0 ( a > 0, a ≠ 1 )

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм. Свойства логарифма (корень логарифма, смена основания).

Корень логарифма из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня/Логарифм. Свойства логарифма (корень логарифма, смена основания).

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

Степень можно выносить за знак логарифма

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a ( f ( x ) 2 = 2 log a f ( x )

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Виды логарифмов

log_a b – логарифм числа b по основанию a ( a > 0, a ≠ 1, b > 0)

lg b – десятичный логарифм (логарифм по основанию 10, a = 10).

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать: Логарифмы с одинаковыми основаниями можно вычитать: Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма: Подставим полученные результаты в исходное выражение:

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,

lg ( x y ) = lg x + lg y ( x > 0, y > 0 )

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e – иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:

log a b = lg b lg a = ln b ln a ( a > 0, a ≠ 1, b > 0 )

Вычисление логарифма равносильно решению показательного уравнения

при условии a > 0, a ≠ 1; b > 0, где

при условии a > 0, a ≠ 1; b > 0, где

Найти логарифм: log ₄ 8

Обозначим log₄ 8 через x :

Перейдем к показательному уравнению:

Сведем показательное уравнение к основе 2 и решим его:

Найти x если : log _x 125 = 3 2

За определением логарифма имеем:

x = (5 3 ) 2/3 = 5 3·2/3 = 5 2 = 25

Формулировки и доказательства свойств

Покажем примеры использования свойства логарифма произведения: log₅(2·3)=log₅2+log₅3 и .

Приведем пример использования этого свойства логарифма: .

Вот пример использования этого свойства: .

Покажем пару примеров применения этого свойства логарифмов: и .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .

Осталось доказать свойства сравнения логарифмов.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

10 примеров логарифмов с решением

1. Найти значение выражения 2. Найти значение выражения 3. Найти значение выражения 3. Найти значение выражения 4. Найти значение выражения 5. Найти значение выражения 5. Найти значение выражения 6. Найти значение выражения Сначала найдем значение Сначала найдем значение Для этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выражения 7. Найти значение выражения Преобразуем наше выражение: Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения 8. Найти значение выражения Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов: 9. Найти значение выражения 9. Найти значение выражения Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выражения Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄: Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник