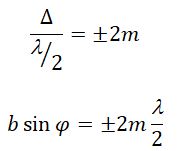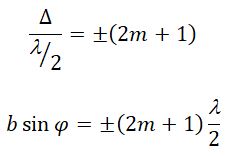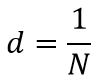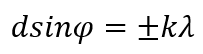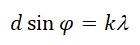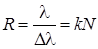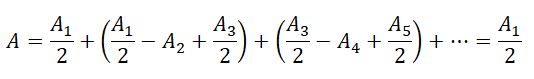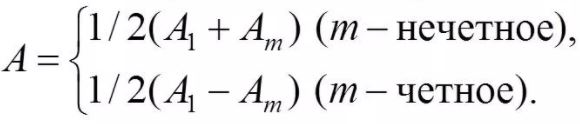в каком случае наблюдается дифракция фраунгофера

В каком случае наблюдается дифракция фраунгофера

§2 Дифракция Фраунгофера на одной щели

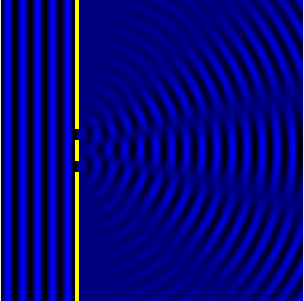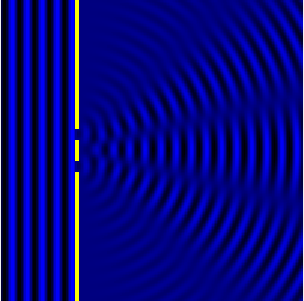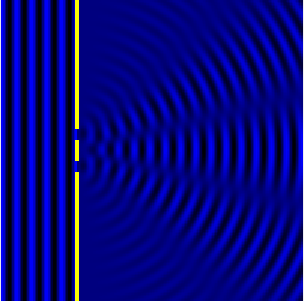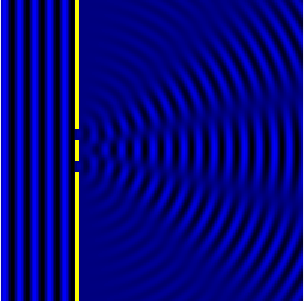
Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.

Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

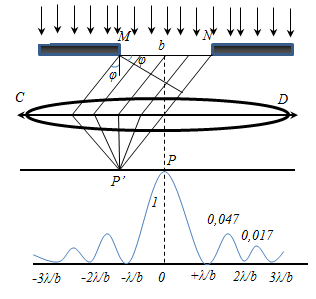
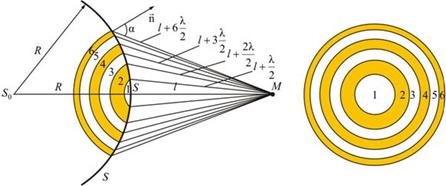
Разобьём волновую поверхность на участке щели М N на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уложится зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля укладывающихся на ширине щели, зависит от угла φ.

Условие минимума при дифракции Френеля:

Если число зон Френеля четное

то в т. Р наблюдается дифракционный минимум.

Если число зон Френеля нечетное

то наблюдается дифракционный максимум.

При φ’=0, Δ = 0 в щели укладывается одна зона Френеля и, следо­вательно, в т. Р главный (центральный) максимум нулевого порядка.

§5 Дифракционная решетка.

Дифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине

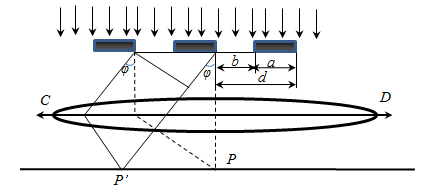
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Т.к. щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки.

(1)

В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае N щелей, т.е. условие главных минимумов дифракционной решетки будет аналогично условию минимумов для щели:

(2)

— условие главных минимумов.

Условие максимумов; те случаи φ, которые удовлетворяют максимумам для одной щели, могут быть либо максимумами, либо минимумами, т.к. всё зависит от разности хода между лучами. Условие главных максимумов:

(3)

Эти максимумы будут расположены симметрично относительно центрального (нулевого k = 0) максимума.

Условие дополнительных максимумов:

Между главными максимума будут располагаться ( N — 1) дополнительных минимумов.

Условие дополнительных минимумов:

Таким образом, дифракционная картина при дифракции на дифракционной решетке будет иметь вид:

Источник

Дифракция Фраунгофера

Дифракция от одной прямоугольной щели

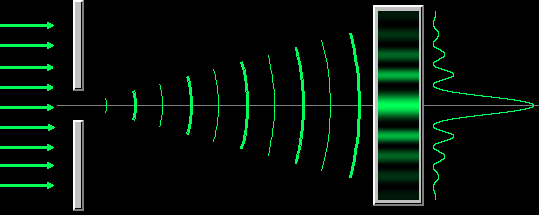
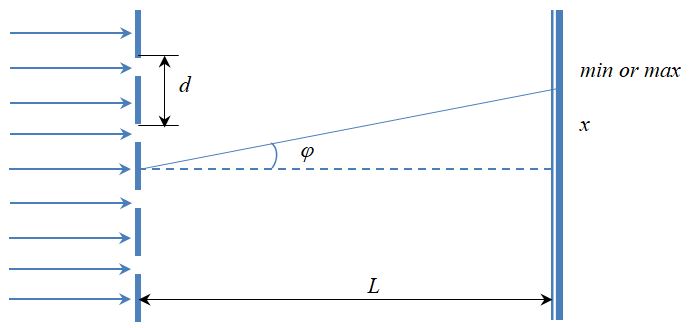
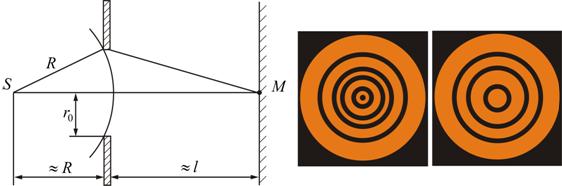
Для наблюдения дифракции Фраунгофера источник света помещают настолько далеко от щели, что лучи можно считать практически параллельными. На практике источник света располагают в фокусе собирающей линзы, тогда лучи, вышедшие из линзы, будут параллельны (рис. 1).

Рис.1.

Площади этих зон одинаковы, поэтому по принципу Гюйгенса-Френеля они испускают волны равной интенсивности. Разность хода между соответствующими точками соседних полосок по построению равна . Поэтому, если в щели укладывается четное число зон Френеля, они попарно друг друга погасят. Тогда в точке B будет наблюдаться минимум, если нечетное, то одна зона окажется непогашенной и в точке B будет максимум.

Число зон Френеля равно . Если это число четное, то мы получаем условие минимума:

,

если нечетное, то условие максимума:

.

Величина называется порядком дифракционного спектра.

В направлении наблюдается самый интенсивный центральный максимум нулевого порядка, в этом случае щель действует как одна зона Френеля и интенсивность света велика.

Если на щель падает белый свет, то для каждой длины волны будет соответствовать свой угол и полоски будут окрашены. Ближе к центру будет фиолетовый свет, конец полоски будет красный. Центральный максимум будет общим для всех длин волн, так что центр дифракционной картина будет представляться в виде белой полоски.

Дифракционная картина зависит от соотношения и :

1. Если , то наблюдается описанная дифракционная картина.

2. Если , то в щели укладывается только одна зона Френеля при всех значениях , и на экране будет наблюдаться расплывшийся нулевой максимум.

3. , . Углы будут мало отличаться для малых . На экране будет видно равномерно освещенное изображение щели и только у краев его размытие (при больших значениях ).

От одной щели трудно наблюдать дифракционную картину из-за малой интенсивности. Поэтому обычно используется дифракционная решетка.

Дифракционная решетка – это система одинаковых параллельных щелей, разделенных равными промежутками (рис. 2).

Рис.2.

Величина называется постоянной дифракционной решетки.

На стеклянную пластинку алмазом наносят царапины. Там где царапина – непрозрачный промежуток решетки. На один миллиметр решетки наносят от 50 до 500 штрихов. Рассмотрим дифракцию от двух щелей (рис. 3).

Рис.3

Если под каким-то углом каждая щель не пропускает свет, то и вся решетка не пропускает (в каждой щели укладывается четное число зон Френеля). Условие главных минимумов для решетки совпадает с условием минимумов для одной щели:

.

Если каждая из щелей дает максимум, то на экране может быть максимум или минимум в зависимости от разности хода лучей . Щели когерентные источники, поэтому лучи интерферируют и дают максимумы или минимумы. Если в величине укладывается четное число полуволн, то наблюдается максимум:

,

если нечетное, то минимум:

.

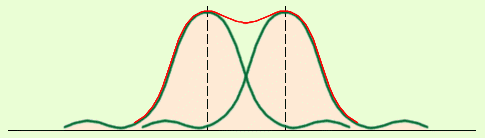
Итак, полная дифракционная картина для двух щелей определяется из условий:

— главные минимумы.

— дополнительные минимумы.

— главные максимумы.

Таким образом, между двумя главными максимумами располагается один дополнительный минимум. Можно показать, что между двумя главными максимумами в случае трех щелей будет располагаться два дополнительных минимума, при четырех щелях – три.

В случае щелей условием дополнительных минимумов будет выражение:

, где .

Число принимает все целочисленные значения, кроме при которых условие дополнительных минимумом переходит в условие главных максимумов.

Следователь но в случае N щелей между двумя главными максимумами располагаются N-1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон. Вторичные или дополнительные максимумами обусловлены интерференцией света от более далеких щелей.

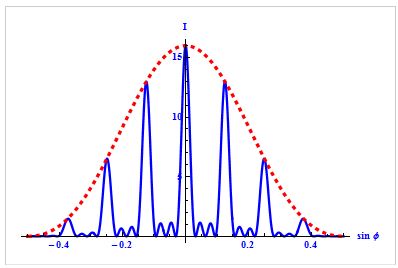
Чем больше щелей, тем больше световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, которые становятся более интенсивными и острыми. На рис. 4. качественно представлена дифракционная картина от восьми щелей.

Рис.4.

Число главных максимумов зависит от отношения периода решетки к длине волны.

отсюда , так как , то .

Полное число максимумов равно: .

Дифракционная решетка используется как спектральный прибор. При пропускании через решетку белого света, все максимумы, кроме главного, разлагаются в спектр (как было уже показано в случае дифракции на одной щели).

Голография в переводе с греческого – полная запись (Голос – весь, грифо – пишу). Голография – это особый способ записи на фотопластинке структуры световой волны, отраженной предметом. При освещении голограммы пучком света эта волна почти полностью восстанавливается и создается впечатление, что наблюдается сам предмет.

Обычный фотографический способ получения изображения предмета основан на регистрации с помощью фотопластинки различий в интенсивности света, рассеваемого разными малыми элементами поверхности предмета. Но при этом не учитывается расстояние, откуда идет свет. В результате получается плоское изображение предмета.

Английский физик Габор (1948) высказал идею принципиально нового метода получения объемных изображений объектов. Он предложил регистрировать при помощи фотопластинки не только интенсивности но и фазы рассеянных предметом волн, воспользовавшись для этого явлением интерференции волн. Распределение интенсивности в интерференционной картине определяется как амплитудой интерферирующих волн, так и разностью их фаз: . Свой метод Габор назвал голографией. Суть метода поясняется на рис. 5.

Рис.5

Лазерный пучок делится на две части, одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны когерентны и они интерферируют на фотопластинке. Интерференционная картина, зафиксированная на фотопластинке после ее проявления, называется голограммой предмета. Голограмма в отличие от фотографического негатива объекта, не имеет внешнего сходства с предметом. Она представляет замысловатый узор из чередующихся малых областей различного почернения эмульсии. Восстановление изображение по его голограмме проясняется на рис.8.

Рис.6

Для восстановления изображения голограмма помещается в тоже положение, где она находилась на стадии получения. Ее освещают опорным пучком того же лазера. Вторая часть лазера перекрывается диафрагмой. В результате дифракции света на интерференционной структуре голограммы образуется два объемных изображения предмета. Одно мнимое, которое находится на том же месте, где был предмет, и действительное висячее.

Мнимое изображение видно при наблюдении сквозь голограмму как через окно. Интерференционная картина в каждой точке голограммы определяется светом, рассеянным всеми точками предмета. Поэтому каждый участок содержит сведения обо всем предмете. С помощью малого осколка голограммы можно восстановить весь предмет. Однако уменьшение размеров голограммы приводит к ухудшению четкости получаемого изображения (чем меньше света, тем меньше света на ней дифрагирует на стадии восстановления изображения).

Применяется голография для записи и хранения информации. На одну и ту же пластинку можно последовательно записать несколько различных голограмм, меняя угол падения опорной волны. На одной фотопластинке можно записать книгу объемом более тысячи страниц. Голография также применяется для кодирования информации. Чтобы восстановить по голограмме изображение предмета нужно точно знать положение фотопластинки при получении голограммы.

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка , что сильно упрощает теоретическое рассмотрение явления. Здесь — расстояние от отверстия или преграды до плоскости наблюдения, — длина волны излучения, а — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).

Источник

В каком случае наблюдается дифракция фраунгофера

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Свойства дифракции:

1) Дифракция волн – характерная особенность распространения волн независимо от их природы.

3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Фраунгофера от одной щели

Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.

Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.

Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:

Дифракционная решетка

Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.

В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:

— условие главных минимумов.

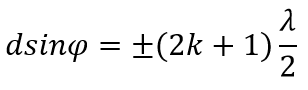
Условие главных максимумов :

Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.

Между главными максимумами будут расположены (N-1) дополнительных минимумов.

Разрешающая способность дифракционной решетки

Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астро­но­ми­ческих приборах реализуется дифракци­он­ный предел качества изо­бра­же­ний. Вслед­ствие дифракционного размытия изобра­жения двух близких точек объекта могут оказаться неотличимыми от изо­бра­же­ния одной точки.

Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ

Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.

Метод зон Френеля

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A₁ + A₂ + A₃ +. + A_i.

где A – амплитуда результирующего колебания, A_i – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина A_i зависит от площади S_i зоны и угла α_i между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

.

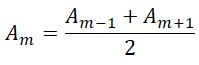
Тогда выражение для амплитуды можно записать в виде

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A₁ /2.

Интенсивность излучения J

Так как радиус центральной зоны мал ( r₁ = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A₁. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J₁ ). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Дифракция на простых объектах

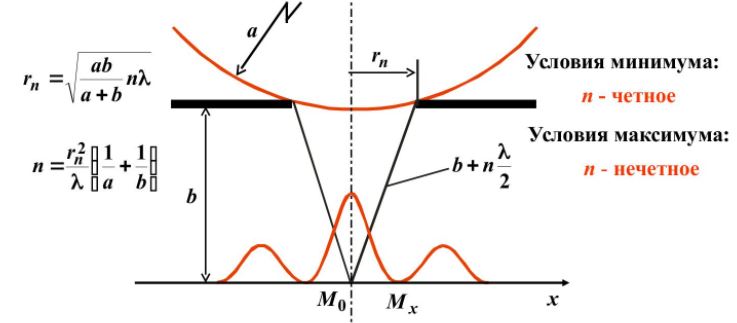
Дифракция на щели

Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.

Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.

Естественно, что если r₀>>λ, то никакой дифракционной картины не будет.

Дифракция от диска
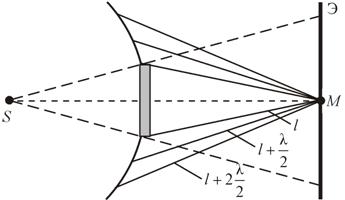
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.

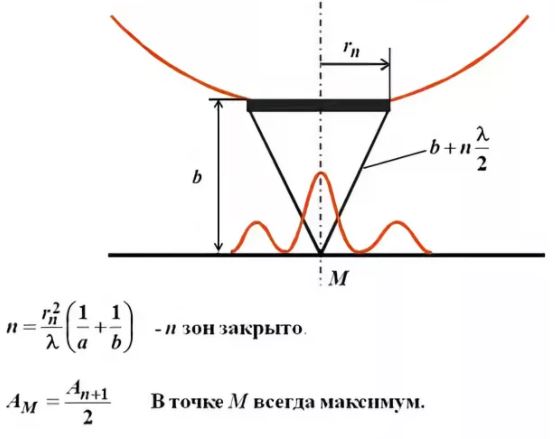
В центре тени светлое пятно

Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.

Источник