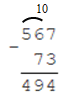в каком случае разность натуральных чисел есть натуральное число

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Октябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Сен
1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

7 класс. Алгебра. Никольский. Учебник. Ответы к стр. 6

Действительные числа
Натуральные числа
Натуральные числа и действия с ними

Ответы к стр. 6

1. Какие числа называют натуральными? Является ли 0 натуральным числом?

Числа 1, 2, 3, 4, 5, … называют натуральными или целыми положительными числами. Нуль не считают натуральным числом.

2. Каким числом является сумма натуральных чисел?

Сумма натуральных чисел является натуральными числом.

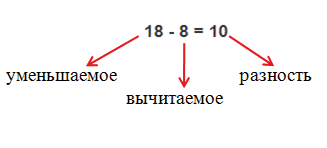
3. В каком случае разность натуральных чисел есть натуральное число?

Разность натуральных чисел является натуральным число только в том случае, если уменьшаемое больше вычитаемого, например: 8 − 5 = 3.

Если уменьшаемое меньше вычитаемого или равно ему, то разность натуральных чисел не является натуральным числом.

4. Каким числом является произведение натуральных чисел?

Произведение натуральных чисел является натуральным числом.

5. Всегда ли выполнимо деление натуральных чисел нацело?

Деление натуральных чисел нацело не всегда выполнимо, например: 7 не делится на 3 нацело.

6. На какие натуральные числа делится нацело любое натуральное число?

Любое натуральное число делится нацело на 1 и само на себя.

7. Делятся ли нацело на 7 числа: 12, 27, 42, 126?

12 − не делится нацело на 7;
27 − не делится нацело на 7;
42 − делится нацело на 7 (42 : 7 = 6);
126 − делится нацело на 7 (126 : 7 = 18).

8. Сформулируйте признак делимости на:
а) 10; б) 5; в) 2; г) 3; д) 9.

а) число делится на 10, если оно оканчивается цифрой 0;
б) число делится на 5, если оно оканчивается цифрой 0 или 5;
в) число делится на 2, если оно оканчивается четной цифрой;
г) число делится на 3, если сумма его цифр делится на 3;
д) число делится на 9, если сумма его цифр делится на 9.

9. Делятся ли нацело на 15 числа: 30, 105, 215, 360?

Число 30 делится нацело на 15, так как 15 = 3 • 5, а по признакам делимости:
— число 30 делится на 3, так сумма его цифр делится на 3 (3 + 0 = 3),
— число 30 делится на 5, так как оно оканчивается на 0;

Число 105 делится нацело на 15, так как 15 = 3 • 5, а по признакам делимости:
— число 105 делится на 3, так сумма его цифр делится на 3 (1 + 0 + 5 = 6),
— число 105 делится на 5, так как оно оканчивается на 5;

Число 215 не делится нацело на 15, так как 15 = 3 • 5, а по признакам делимости:
— число 215 не делится на 3, так сумма его цифр не делится на 3 (2 + 1 + 5 = 8);

Число 360 делится нацело на 15, так как 15 = 3 • 5, а по признакам делимости:
— число 360 делится на 3, так сумма его цифр делится на 3 (3 + 6 + 0 = 9),
— число 360 делится на 5, так как оно оканчивается на 0.

10. Делятся ли нацело на 18 числа: 189, 252, 456, 1998, 1999?

Число 189 не делится нацело на 18, так как 18 = 2 • 9, а по признакам делимости:
— число 189 не делится на 2, так как оно не оканчивается четной цифрой;

Число 252 делится нацело на 18, так как 18 = 2 • 9, а по признакам делимости:
— число 252 делится на 2, так оно оканчивается на четное число,
— число 252 делится на 9, так как сумма его цифр делится на 9 (2 + 5 + 2 = 9);

Число 456 не делится нацело на 18, так как 18 = 2 • 9, а по признакам делимости:
— число 456 не делится на 9, так как сумма его цифр не делится на 9 (4 + 5 + 6 = 15);

Число 1998 делится нацело на 18, так как 18 = 2 • 9, а по признакам делимости:
— число 1998 делится на 2, так оно оканчивается на четное число,
— число 1998 делится на 9, так как сумма его цифр делится на 9 (1 + 9 + 9 + 8 = 27);

Число 1999 не делится нацело на 18, так как 18 = 2 • 9, а по признакам делимости:
— число 1999 не делится на 9, так как сумма его цифр не делится на 9 (1 + 9 + 9 + 9 = 28).

11. Какие из чисел 3124, 3582, 3528, 31 212 делятся на 4?

Число делится на 4, если его две последние цифры образуют число, которое делится на 4:
3124 − делится на 4, так как 24 : 4 = 6;
3582 − не делится на 4, так как 82 не делится на 4;
3528 − делится на 4, так как 28 : 4 = 7;
31 212 − делится на 4, так как 12 : 4 = 3.

12. Делятся ли нацело на 45 числа: 234, 900, 954, 5553, 3555?

Число 234 не делится нацело на 45, так как 45 = 5 • 9, а по признакам делимости:
— число 234 не делится на 5, так оно не оканчивается ни на 0, ни на 5;

Число 900 делится нацело на 45, так как 45 = 5 • 9, а по признакам делимости:
— число 900 делится на 5, так оно оканчивается на 0,
— число 900 делится на 9, так как сумма его цифр делится на 9 (9 + 0 + 0 = 9);

Число 954 не делится нацело на 45, так как 45 = 5 • 9, а по признакам делимости:
— число 954 не делится на 5, так оно не оканчивается ни на 0, ни на 5;

Число 5553 не делится нацело на 45, так как 45 = 5 • 9, а по признакам делимости:
— число 5553 не делится на 5, так оно не оканчивается ни на 0, ни на 5;

Число 3555 делится нацело на 45, так как 45 = 5 • 9, а по признакам делимости:
— число 3555 делится на 5, так оно оканчивается на 5,
— число 3555 делится на 9, так как сумма его цифр делится на 9 (3 + 5 + 5 + 5 = 18).

13. Какие из чисел 5425, 3530, 3550, 31 275 делятся на 25?

Число делится на 25, если его две последние цифры образуют число, которое делится на 25:
число 5425 делится на 25, так как 25 : 25 = 1;
число 3530 не делится на 25, так как 30 не делится на 25;
число 3550 делится на 25, так как 50 : 25 = 2;
число 31 275 делится на 25, так как 75 : 25 = 3.

Вычислите (14-15):

14. а) 7326 + 359; б) 5321 − 985; в) 424 • 27;
г) 15 795 : 39; д) 732 • 254 − 8145 : 45 + 314 253.

д) 732 • 254 − 8145 : 45 + 314 253 = 185 928 − 181 + 314 253 = 185 747 + 314 253 = 500 000

15. а) 329 • 759 + 329 • 41; б) 724 • 928 − 724 • 128;
в) 398 • 801 − 398; г) 854 • 399 + 854.

а) 329 • 759 + 329 • 41 = 329 • (759 + 41) = 329 • 800 = 263 200;

б) 724 • 928 − 724 • 128 = 724 • (928 − 128) = 724 • 800 = 579 200;

в) 398 • 801 − 398 = 398 • (801 − 1) = 398 • 800 = 318 400;

г) 854 • 399 + 854 = 854 • (399 + 1) = 854 • 400 = 341 600.

16. Объясните, не выполняя всех вычислений, почему:
а) 357 • 828 + 357 • 936 делится на 357;
б) 425 • 723 − 315 • 723 делится на 3; на 5; на 15.

а) 357 • 828 + 357 • 936 = 357 • (828 + 936) − делится на 357, так как один из множителей (357) делится на 357;

б) 425 • 723 − 315 • 723 = 723 • (425 − 315) = 723 • 110 — делится:
на 3, так как один из множителей (723) делится на 3;
на 5, так как один из множителей (110) делится на 5;
на 15, так как 15 = 3 • 5, и один из множителей (723) делится на 3, а второй множитель (110) делится на 5.

Источник

Вычитание натуральных чисел

Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!

Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.

Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.

Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.

Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.

Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.

Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.

Связь вычитания и сложения

Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.

Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.

Свойства разности натуральных чисел

Свойства разности натуральных чисел состоят из:

Рассмотрим каждый пункт подробнее.

Правила вычитания суммы из числа и числа из суммы

Как вычесть сумму из числа

Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.

Рассмотрим это на примере из урока сложение чисел.

325 +( 12 + 64 + 5 ) = 325 +81 = 406

Я запишу это в виде разности:

и покажу, что результат будет равен первому слагаемому:

Как видите, все верно.

Как вычесть число из суммы

Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.

Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.

Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:

325 +81 = ( 191 + 65 + 150 )

Превращаю выражение в разность:

( 191 + 65 + 150 )-81 = 325

и покажу, что результат также будет равен первому слагаемому:

Как меняется разность при изменении вычитаемого или уменьшаемого

Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.

Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.

Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.

Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.

Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.

Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.

Правила вычитания разности

Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.

Это свойство выводится из предыдущих, рассмотренных нами.

22 — 17 = 5

5+ 3 = 8

22 +3-( 17 +3- 3 )

25- 17 +0 = 8

Как видите, оба способа показали верный результат.

Вычитание однозначного числа

Вычитание в столбик многозначных чисел

Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.

После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:

50063-4825 = 45238.

Как проверить действия сложение и вычитание?

Проверить сложение можно двумя способами: обратным сложением и вычитанием.

Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.

Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.

И этот способ проверки показал правильность нашего решения.

Проверить вычитание также возможно и сложением, и другим вычитанием.

Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.

Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238 :

Источник

Вычитание натуральных чисел

Понятие «вычитание»

Обозначения

Свойства вычитания натуральных чисел

1) При вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.

2) Разность показывает на сколько больше уменьшаемое больше вычитаемого.

34 больше, чем 7 на 17 единиц.

3) Если вычитаемое равно 0, разность равна уменьшаемому.

4) Если от любого числа вычесть 1, то получим число предшествующее данному.

5) Вычитание натурального числа из суммы натуральных чисел.

Чтобы вычесть натуральное число из суммы натуральных чисел, необходимо сначала сложить числа, а затем вычесть данное натуральное число, или первым действием вычесть данное натуральное число из любого слагаемого, а к разности прибавить оставшееся слагаемое.

6) Вычитание суммы чисел из натурального числа.

Чтобы вычесть сумму чисел из натурального числа, необходимо сначала сложить два числа, после этого вычесть полученную сумму из данного числа, или вычесть из данного числа любое из слагаемых, поле этого вычесть второе.

Вычитание чисел с разными разрядами

Для того чтобы вычесть числа с разным разрядом, необходимо разложить числа по разрядам.

567 = 500 + 60 + 7 = 400 + 100 + 60 + 7

Из единиц вычтем единицы, из десятков десятки, из сотен сотни и т.д.

Поскольку из 60 нельзя вычесть 70, разложим 500 на 400 и 100, прибавим 100 к 60

Полученное число: 400 + 90 + 4 = 494.

Вычитание в столбик

Многозначные числа удобнее всего вычитать в столбик. Для того чтобы вычесть число из числа в столбик, необходимо:

1. Правильно записать числа. Первым записываем уменьшаемое, под уменьшаемым пишем вычитаемое, так чтобы каждый разряд вычитаемого находился строго под соответствующим разрядом вычитаемого. Слева поставим знак «-» под столбиком, состоящим из уменьшаемого и вычитаемого проводим черту

2. Справа налево последовательно вычитаем из разряда уменьшаемого соответствующий разряд вычитаемого. Результат запишем под чертой, это будет разность.

3 Если разряд уменьшаемого окажется меньше разряда вычитаемого занимаем 10 у разряда стоящего слева (см. рисунок).

Вычитание с помощью координатного луча

Для вычитания с помощью координатного луча, отметим точку соответствующую уменьшаемому, в нашем примере, это число 12. Для вычитания отсчитываем влево количество единичных отрезков равных вычитаемому (8). Получившаяся точка будет являться разницей (4).

Поделись с друзьями в социальных сетях:

Источник

Натуральные числа и нуль

Видеоурок по этой теме можно посмотреть по ссылке: Натуральные числа и ноль.

Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!

Нас повсюду окружают предметы. Так было раньше, и так будет всегда. И очень часто необходимо знать, сколько у нас или где-то еще есть тех или иных предметов: яблок, машин, людей, денег и т.д.

Еще в очень глубокой древности, когда не было не только науки математики, но и даже такого понятия как число, древние люди проводили подсчет при помощи наиболее близких для них инструментов – собственных частей тела: «Там столько буйволов, сколько на моих руках пальцев», или: «Мы поймали рыбы столько, сколько пальцев на руках у меня и тебя».

Со временем они заметили, что десять буйволов, десять рыб, десять врагов и т.д. объединяет то, что рассказывая об этом, люди употребляют одинаковое описание: «сколько на моих руках пальцев». То есть, они обнаружили, что группы разных предметов обладают одним схожим свойством – количеством, и что удобнее назвать одинаковое количество чего-либо обобщенным названием, которое будет определять эту величину. И вместо: «Мы поймали столько рыбы, сколько пальцев на моих руках» люди начали говорить: «Мы поймали десять рыб». Так появились числа, которые впоследствии были названы натуральными. Подробнее об истории возникновения чисел можно почитать по ссылке.

Натуральные числа – это те числа, при помощи которых мы осуществляем счет предметов: 1, 2, 3, 4, 5 и т.д

Число 1 (один) имеет еще одно название: единица.

Если к единице приложить еще единицу, к получившемуся результату еще одну, потом еще, и еще и т.д., то мы получим ряд натуральных чисел или просто натуральный ряд: один, два, три, четыре, пять и т.д.

Любое натуральное число можно представить в виде единицы или собрания нескольких единиц.

Начинается натуральный ряд чисел с единицы, то есть, с числа 1 (один).

Каждое последующее число ряда отличается от предыдущего на единицу.

Любое натуральное число больше нуля.

Нуль не относится к натуральному ряду чисел. В некоторых англоязычных странах его включают в этот ряд, но в отечественной математике принято по-другому. Действительно, нуль означает отсутствие чего-либо, «ни одной единицы», «ни одного», «ничего». А поскольку ряд натуральных чисел состоит из единицы и совокупности сложений единиц, то число «ни одной единицы» не может находиться в этом ряду.

Нуль обладает такими свойствами:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.8 / 5. Количество оценок: 6

Источник

Натуральные числа. Ряд натуральных чисел.

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.

Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.

Источник