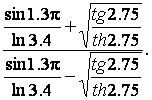в какую переменную помещается результат после ввода выражения

Примечание
После ключевого слова collect допускается задание нескольких переменных через запятую. В этом случае, что иллюстрируется последней строкой листинга 5.6, приведение подобных слагаемых выполняется последовательно по всем переменным.

Рис. 5.10. Вычисление коэффициентов полинома

Примечание
Конкретная задача, требующая вычисления полиномиальных коэффициентов, приведена в разделе, посвященном численному отделению корней полинома (см. разд. «Корни полинома»гл. 8).

Примечание
Символьный поиск предела функции описан в разд. «Вычислительные операторы» гл. 3).

Рис. 5.14. Интегрирование по переменной

Примечание
Более подробную информацию о символьном решении алгебраических уравнений, дифференцировании и интегрировании (с применением оператора символьного вывода), включая вычисление производных высших порядков, определенных кратных интегралов, можно найти в части 3 этой книги (см. гл. 7).

Рис. 5.15. Подготовка выражения для разложения в ряд по переменной х
4. В появившемся диалоговом окне (рис. 5.16) введите желаемый порядок аппроксимации (Order of Approximation) и нажмите кнопку ОК.
Результат разложения появится под выражением (рис. 5.17).
Не забывайте, что разложение строится только в точке х=0. Чтобы получить разложение в другой точке х=а, можно, к примеру, подставить вместо переменной х значение х-а (см. разд. 5.2.8).

Рис. 5.16. Разложение в ряд Тейлора

Рис. 5.17. Результат разложения в ряд Тейлора
Для разложения в ряд альтернативным способом, с помощью оператора символьного вывода, используйте ключевое слово series, вставляя его одноименной кнопкой панели Symbolic (Символика). После ключевого слова series, через запятую, указывается имя переменной, по которой производится разложение, и порядок аппроксимации (листинги 5.13 и 5.14). Сравнение функции и ее разложений в ряды с разными порядками аппроксимации (для k=b=i) иллюстрируется рис. 5.18. Видно, что разложение в ряд хорошо работает в окрестности точки х=о, а по мере удаления от нее все сильнее и сильнее отличается от функции.
Листинг 5.13. Разложение выражения в ряд с разным порядком
аппроксимации

Пистинг 5.14. Разложение выражения в ряд по разным переменным

Примечание
Подробная информация о символьном решении алгебраических уравнений изложена в части III (см. гл. 8). В частности, там рассказано о возможности решения систем уравнений и задании уравнений в привычной для нас форме логического равенства.

Рис. 5.20. Расчет Фурье-преобразования при помощи меню
Аналитический расчет преобразования Фурье при помощи меню показан на рис. 5.20. В листинге 5.15 приведены два примера вычисления прямого преобразования Фурье с применением ключевого слова fourier и оператора символьного вывода Листингом 5.16 иллюстрируется обратное преобразование Фурье одной из функций предыдущего листинга.

Примечание
В MathCAD преобразование Фурье можно вычислить и с помощью численного процессора, использующего популярный алгоритм БПФ (см. разд. «Преобразование Фурье»гл. 14).

Совет
Используйте меню Symbolics (Символика), если требуется «сиюминутно» провести некоторые аналитические действия с выражением и получить ответ в общем виде, не учитывающем текущие значения переменных, входящих в выражение.

Рис. 5.21. Вычисление выражения с плавающей точкой
Еще один пункт меню Symbolics / Evaluate / Complex (Символика / Вычислить / Комплексно) позволяет представить выражение в виде а+b*i
Аналогичные по действию ключевые слова float и complex можно использовать в документах, вводя их с панели Symbolic (Символика). Ключевое слово float применяется вместе со значением точности вывода результата с плавающей точкой (листинг 5.21). С помощью слова complex можно преобразовывать выражения как в символьном виде, так и с учетом численных значений, если они были ранее присвоены переменным (несколько примеров)
Листинг 5.21. Вычисление выражения с плавающей точкой

Листинг 5.22. Комплексные преобразования выражений

5.5.3. Последовательности символьных команд
Символьные вычисления допускается проводить с применением цепочек из ключевых слов. Для этого ключевые слова, соответствующие последовательным символьным операциям, должны быть введены по очереди с панели Symbolic (Символика). Принцип организации цепочек символьных вычислений очень похож на применение встроенного языка программирования MathCAD (см. следующую главу). Несколько примеров использования последовательности символьных операторов приводится в листингах 5.23 и 5.24.

Примечание
Последовательности символьных команд допускают введение дополнительных условий в расчеты, например, таких как ограничение на действительную или комплексную форму результата. Это делается с помощью ключевого слова assume. Более подробную информацию читатель найдет в справочной системе MathCAD.

Листинг 5.23. Фурье-преобразование, разложение в ряд и расчет

Листинг 5.24. Z-преобразование и разложение на простые дроби

Источник

В какую переменную помещается результат после ввода выражения

Г лава 1. Начало работы с MathCAD

1.6 Переменные и функции

Основные инструменты математика – это операции с переменными величинами и функциями. В MathCAD переменные, операторы и функции реализованы в интуитивной форме, т. е. выражения в редакторе вводятся и вычисляются так, как они были бы написаны на листе бумаги. Порядок вычислений в документе MathCAD также очевиден: математические выражения и действия воспринимаются процессором слева направо и сверху вниз.

Перечислим основные действия, которые пользователь может совершать для определения и вывода переменных и функций.

Чтобы определить переменную, достаточно ввести ее имя и присвоить ей некоторое значение, для чего служит оператор присваивания.
Присваивание переменным значений

Чтобы присвоить переменной новое значение, например переменную х сделать равной 10:

1. Введите в желаемом месте документа имя переменной, например х.

2. Введите оператор присваивания с помощью клавиши или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator (Калькулятор) или Evaluation (Выражения), как показано на рис. 1.22

3. Введите в появившийся местозаполнитель новое значение переменной (10).

Рис. 1.22 Результат ввода оператора присваивания

Кнопка оператора присваивания для удобства помещена сразу на две панели Calculator (Калькулятор) и Evaluation (Выражения).

Ввести новое значение переменной возможно как в виде числа, так и в виде математического выражения, содержащего другие переменные (рис. 1.23) и функции, а также в виде строкового выражения (рис. 1.24). В последнем случае будет создана переменная s не численного, а строкового типа.

Рис. 1.23 Присваивание переменной вычисленного значения выражения

Рис. 1.24 Присваивание переменной строкового значения

Если переменная с некоторым именем создается в данном документе впервые, то для ввода оператора присваивания, вместо двоеточия, допускается использовать символ равенства «=», который MathCAD автоматически заменит символом присваивания.

В некоторых случаях это невозможно, в частности когда значение присваивается переменной, имя которой зарезервировано MathCAD. Например, присвоить значение переменной с именем N можно, лишь вводя двоеточие, т. к. по умолчанию это имя обозначает в MathCAD размерность силы (Ньютон).

Чтобы переопределить значение переменной, определенной в документе, оператор присваивания следует вводить не знаком равенства, а двоеточием, либо пользоваться панелью инструментов.

Не вполне соответствующий общепринятому математическому стилю вид оператора присваивания (не =, а :=) является, на самом деле, компромиссом, связанным с назначением MathCAD как системы программирования. Этот оператор показывает, что он действует, в отличие от других, не слева направо, а справа налево, поскольку значение (справа) задается переменной (слева). И если непосвященного математика внешний вид этого оператора может ввести в некоторое заблуждение, то пользователю MathCAD он прямо говорит о действии, выполняемом в данном месте документа: значение переменной не выводится на экран (о чем говорит знак =), а некоторое значение присваивается (:=) данной переменной.

Для подготовки отчетов, тем не менее, может потребоваться изменить отображение оператора присваивания с принятых по умолчанию символов «:=» на символ равенства. Это делается для конкретного оператора присваивания с помощью пункта View Definition As контекстного меню (рис. 1.25), либо для всего документа с помощью команды Math / Options / Display (Математика / Опции / Отображение).

Рис.1.25 Различное отображение оператора присваивания

Помимо разобранного оператора присваивания (а он применяется наиболее часто), существует также возможность глобального присваивания.

Функции в MathCAD записываются в обычной для математика форме:

– х. – список переменных.

Легче всего ввести написание функции в документ при помощи клавиатуры. В MathCAD формально можно разделить функции на два типа:

– функции, определенные пользователем.

Определение функции пользователя

Для того чтобы определить функцию пользователя, например f(x,y) = x 2 *cos (x+y):
1. Введите в желаемом месте документа имя функции (f).

Все переменные, присутствующие справа в выражении определения функции, либо должны входить в список аргументов функции (в скобках, слева после имени функции), либо должны быть определены ранее. В противном случае будет выведено сообщение об ошибке, причем имя неопределенной переменной будет выделено красным цветом (рис. 1.26).

Рис. 1.26 Сообщение об ошибке («Эта переменная или функция ранее не определена»)

Вывод значений переменных и функций

Чтобы вычислить в документе некоторое математическое выражение, которое может состоять из переменных, операторов и функций (встроенных и определенных пользователем):

1. Введите это выражение, например ху;

В результате справа от введенного знака равенства появится вычисленное значение выражения (листинг 3.5, предпоследняя строка). Нельзя изменять содержимое выражения справа от знака равенства, поскольку оно есть результат работы вычислительного процессора MathCAD, совершенно скрытой от глаз пользователя. Подчас (когда выражение содержит функции, реализующие разные численные методы, часто в сложных комбинациях) алгоритмы расчета бывают очень затейливыми и занимают существенное время. О том, что некоторое выражение документа находится в стадии вычисления, свидетельствует обрамляющая его зеленая рамка и невозможность предпринять какое-либо действие с программой MathCAD.

Рассмотрим пример вычисление выражения

Заметьте, что перед тем как вычислить значение математического выражения, вы обязаны определить значение каждой входящей в него переменной (две первых строки). Вычисляемое выражение может содержать любое количество переменных, операторов и функций. Вывод текущего значения той или иной переменной приведен в последней строке примера, а значения функции:

Вводя знак равенства для вычисления математических выражений в MathCAD, вы фактически применяете оператор вычисления, или численного вывода (numerical evaluation). Его можно ввести также нажатием кнопки со знаком равенства на одной из панелей инструментов: Calculator (Калькулятор) или Evaluation (Выражения). Оператор численного вывода означает, что все вычисления проводятся с числами, а различные встроенные алгоритмы реализуются соответствующими численными методами.

Наряду с численным выводом, в MathCAD имеется возможность символьного, или аналитического, вычисления значения выражения. Для символьных вычислений имеется ряд специальных средств, которые будут детально рассмотрены позднее (см. гл. 2), самое простое из них – это оператор символьного вывода (symbolic evaluation). Он обозначается символом → и в большинстве случаев применяется точно так же, как оператор численного вывода, однако внутреннее различие между действием этих двух операторов огромно. Если численный вывод – это в обычном смысле этого слова «запрограммированный» расчет по формулам и численным методам, скрытый от глаза пользователя, то символьный вывод – результат работы системы искусственного интеллекта, встроенной в MathCAD и называемой символьным процессором. Работа символьного процессора также невидима (и, чаще всего, даже трудно представима) пользователю и заключается в анализе самого текста математических выражений. Конечно, гораздо более узкий круг формул можно рассчитать символьно, хотя бы потому, что, вообще говоря, относительно не такая большая часть математических задач допускает аналитическое решение.

Допустимые имена переменных и функций

Перечислим, какие символы можно, а какие нельзя применять в именах, которые пользователь дает переменным и функциям, и перечислим ряд ограничений на присваивание имен. Допустимые символы:
– большие и маленькие буквы – MathCAD различает регистр: так, имена х и х определяют разные переменные. Кроме того, MathCAD различает и шрифт, например имена х и х воспринимаются как разные;

– символ бесконечности (клавиши + + );

Теперь рассмотрим ограничения на имена переменных и функций:
– имя не может начинаться с цифры, символа подчеркивания, штриха или процента;
– символ бесконечности должен быть только первым в имени;

– все буквы в имени должны иметь один стиль и шрифт;

– имена не могут совпадать с именами встроенных функций, констант и размерностей, например, sin или TOL. Тем не менее, допускается их переопределение, но тогда одноименная встроенная функция больше не будет использоваться по первоначальному назначению;

– MathCAD не различает имен переменных и функций: если сначала определить функцию f (х), а потом переменную f, то в оставшейся части документа будет утерян доступ к функции f(x).
В некоторых случаях желательно использовать имена переменных и функций, содержащие символы операторов MathCAD или другие символы, которые нельзя вставлять в имена непосредственно. Для этого существуют две возможности.
Во-первых, имя, составленное из любых символов и заключенное в квадратные скобки, MathCAD будет воспринимать корректно (рис. 1.27, сверху). Например, чтобы ввести имя [а+b]

2. Введите в местозаполнитель последовательность любых символов, например а+b.

Рис. 1.27 Специальные символы в именах переменных

Во-вторых, если вас не устраивает наличие квадратных скобок в имени, то вставить в него специальные символы можно чуть более сложным способом. Например, для ввода имени а+b:

1. Введите первый символ (а), который должен быть допустимым для имен MathCAD.

2. Нажмите клавиши + + для перехода в специальный «текстовый» режим редактирования.

3. Введите последовательность любых символов (+).

Результат этих действий показан в нижней строке рис. 1.27. Если требуется, чтобы имя начиналось со специального символа (средняя строка рис. 1.27), то необходимо выполнить все пункты 1–4, вводя в начале имени произвольный допустимый символ, а по завершении ввода просто стирая его.

Источник

Как и во всех языках программирования, в MatLab предусмотрена возможность работы с переменными. Причем пользователь не должен заботиться о том, какие значения будет принимать переменная (комплексные, вещественные или только целые). Для того чтобы присвоить, например, переменной z значение 1.45, достаточно написать в командной строке z = 1.45, при этом MatLab сразу же выведет значение z:

Здесь знак равенства используется в качестве оператора присваивания. Часто не очень удобно после каждого присваивания получать еще и результат. Поэтому в MatLab предусмотрена возможность завершать оператор присваивания точкой с запятой для подавления вывода результата в командное окно. Именем переменной может быть любая последовательность букв и цифр без пробела, начинающаяся с буквы. Строчные и прописные буквы различаются, например MZ и mz являются двумя разными переменными. Количество воспринимаемых MatLab символов в имени переменной составляет 31.
В качестве упражнения на использование переменных найдите значение следующего выражения:

Наберите последовательность команд, приведенную ниже (обратите внимание на точку с запятой в первых двух операторах присваивания для подавления вывода промежуточных значений на экран):

Последний оператор присваивания не завершается точкой с запятой для того, чтобы сразу получить значение исходного выражения. Конечно, можно было бы ввести сразу всю формулу и получить тот же результат:

Обратите внимание, насколько первая запись компактнее и яснее второй! Во втором варианте формула не помещалась в командном окне на одной строке, и пришлось записать ее в две строки, для чего в конце первой строки поставлены три точки.

Для ввода длинных формул или команд в командную строку следует поставить три точки (подряд, без пробелов), нажать клавишу и продолжить набор формулы на следующей строке. Так можно разместить выражение на нескольких строках. MatLab вычислит все выражение или выполнит команду после нажатия на в последней строке (в которой нет трех идущих подряд точек).

MatLab запоминает значения всех переменных, определенных во время сеанса работы. Если после ввода примера, приведенного выше, были проделаны еще какие-либо вычисления, и возникла необходимость вывести значение х, то следует просто набрать х в командной строке и нажать :

Переменные, определенные выше, можно использовать и в других формулах. Например, если теперь необходимо вычислить выражение

,

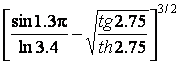
то достаточно ввести следующую команду:

Вызов функций в MatLab обладает достаточной гибкостью. Например, вычислить е3.5 можно, вызвав функцию ехр из командной строки:

Другой способ состоит в использовании оператора присваивания:

Предположим, что часть вычислений с переменными выполнена, а остальные придется доделать во время следующего сеанса работы с MatLab. В этом случае понадобится сохранить переменные, определенные в рабочей среде.

Просмотр переменных

При работе с достаточно большим количеством переменных необходимо знать, какие переменные уже использованы, а какие нет. Для этой цели служит команда who, выводящая в командное окно MatLab список используемых переменных:

» who
Your variables are:
al a2 a3

Команда whos позволяет получить более подробную информацию о переменных в виде таблицы:

Источник

В какую переменную помещается результат после ввода выражения

Глава 2. Символьное вычисление

2.1 Использование символьной панели инструментов

Символьная панель инструментов вызывается из математической панели щелчком на значке Symbolic Keyword Toolbar (значок с изображением шапочки академика). Содержание панели показано на рис. 2.1.

Рис. 2.1 Символьная панель инструментов

В MathCAD существует символьный знак равенства → – он вводится с клавиатуры сочетанием клавиш Ctrl +.(точка) или с панелей Symbolic Keyword Toolbar (Панель вычислений). В отличие от обычного знака равенства, символьный знак равенства возвращает не число, а выражение.

При использовании меню Symbolics MathCAD игнорирует предыдущие определения всех величин, входящих в рассматриваемое выражение, и не учитывает функции пользователя.

При использовании символьного равенства и панели инструментов Symbolic MathCAD учитывает все предыдущие определения и при пересчете всей программы пересчитывает и результат символьных вычислений и работает с функциями пользователя.

На символьной панели инструментов (см. рис. 2.1) есть два символьных знака равенства: с одним местом ввода и с двумя местами ввода. Одно место ввода предназначено для ввода выражения или функции (встроенной или пользователя), второе – для ввода ключевого слова, означающего выполняемое действие.

Символьный знак равенства с двумя местами ввода позволяет создавать программы символьных вычислений, включающих в себя несколько последовательных действий.

Команды, их шаблоны и действие команд приведены в табл. 2. В ней жирные точки обозначают места ввода выражений (слева) и ключевых слов (справа).

Таблица 2 Действия, выполняемые с помощью ключевых слов

Вычисления с плавающей точкой

Возвращает комплексное число

Раскрытие степеней и произведений, сумм нескольких переменных

Решение уравнений и систем уравнений для указанной после запятой переменной

Упрощение выражений

Вычисление выражений с подстановкой определенных значений или с заменой переменной

Упрощение выражений представлением их суммой простых полиномов

Разложение выражений в степенной ряд. Число членов вводится в правое поле ввода

Вычисление с присвоением определенных значений переменных

Разложение выражения на простые дроби

Определение вектора коэффициентов полинома

Разложение выражения на произведения

Прямое преобразование Фурье

Прямое преобразование Лапласа

Прямое z – преобразование

Обратное преобразование Фурье

Обратное преобразование Лапласа

Обратное z – преобразование

Транспонирование матрицы

Вычисление определителя матрицы

Подстановка числовых значений и размерностей в формулу

Употребляются в сочетании с другими словами

Упрощает выражение с ехр или ln

Разложение непрерывной дроби на фракции

Переписывает выражение с указанными элементарными функциями

Вывод панели Modifier

Символьное интегрирование и дифференцирование

Рис. 2. 2 Символьные вычисления с одноместным знаком равенства

Символьные вычисления начинают с ввода исходного выражения, подлежащего преобразованию:

· Для выполнения команды simplify и для вычисления интегралов, производных, сумм и произведений выберите на символьной панели инструментов одноместный знак символьного равенства.

· Для выполнения других символьных операций после ввода выражения нажмите на символьной панели инструментов кнопку с названием необходимой операции. В появившемся на экране шаблоне заполните нужные места ввода и удалите ненужные.

· Для одновременного выполнения нескольких символьных операций выберите на панели инструментов двухместный знак символьного равенства. В появившемся шаблоне заполните нужные места ввода и удалите ненужные.

При использовании двухместного символьного знака равенства после ввода каждого ключевого слова с названием символьной операции. После ввода всех символьных операций надо удалить лишние места ввода и автоматически появляющиеся лишние скобки.

· Для вывода результатов символьных вычислений выведите курсор за пределы выражения и нажмите левую кнопку мыши.

Рис. 2. 3 Использование функций пользователя в символьных вычислениях

Для символьного решения уравнений и неравенств на символьной панели инструментов нужно выбрать команду solve (Решить). При этом на экране появляется символьный знак равенства с местом ввода, где надо указать переменную, относительно которой решается уравнений или неравенство (см. рис. 2. 3).

Для символьного решения уравнений можно использовать функцию root и вычислительный блок Given – find (рис.5.23,5.24 и 5.27). При этом для вывода результата используется одноместный символьный знак равенства → (клавиши Ctrl +.). В MathCAD 13 и 14 функция root не позволяет решить уравнения символьно.

При использовании команды substitute (Заменить) необходимо задать вариант подстановки. Если нужно заменить не одну переменную, а несколько, то второй и последующие варианты подстановки вводятся запятую и набираются с клавиатуры.

Ключевое слово assume позволяет ввести ограничения на значения переменных, что бывает необходимо, если, например, функция имеет разрыв в некоторой точке (см. рис. 2. 4).

Рис. 2. 4 Использование различных команд символьной панели инструментов

При разложении в ряд Тейлора (команда series ) необходимо указать координаты точки, в окрестности которой производится разложение, и число членов ряда. Если не указать это число, то MathCAD по умолчанию выводит результат с шестью членами ряда Тейлора.

Использование нескольких команд одновременно – довольно сложный процесс, так как надо знать, может ли быть преобразован промежуточный символьный результат. Чтобы убедиться в этом, его надо увидеть, то есть вывести каждый результат отдельно.

Одноместные символьный знак равенства позволяет выполнить различные операции с массивами. Кроме трех функций (транспонирование, обращение и вычисления определителя матрицы), находящихся на символьной панели инструментов, можно выполнять операции сложения, вычитания и перемножения матриц, а также использовать встроенные функции для работы с матрицами, например, для нахождения собственных чисел ( eigenvals ) и собственных векторов ( eig е nvecs ) (рис. 2. 5 и 2. 6).

Решение матричного уравнения А*Х=С

Рис. 2. 5 Символьные операции с массивами

Возможность получения символьного решения почти любого матричного выражения является большим достоинством MathCAD.

отключено, большое выражение

Рис. 2. 6 Символьное определение собственных чисел и собственных векторов матрицы

Источник