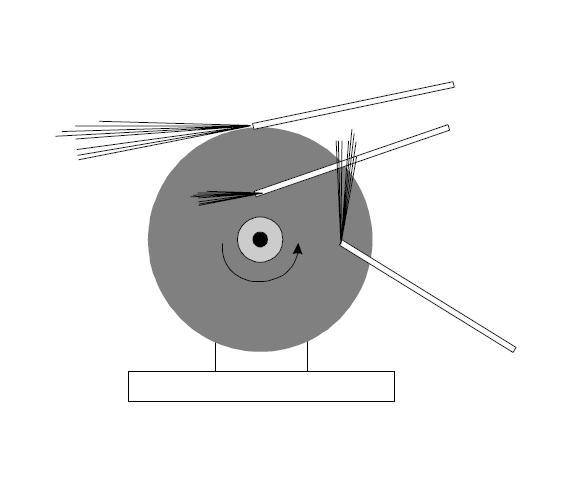
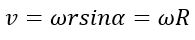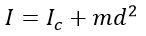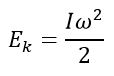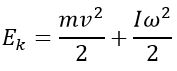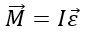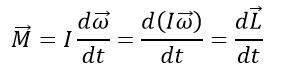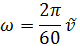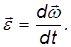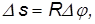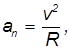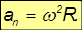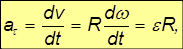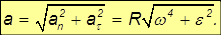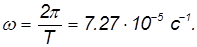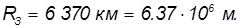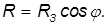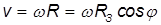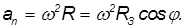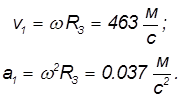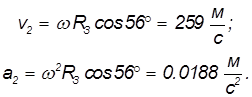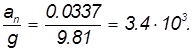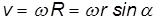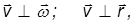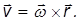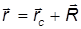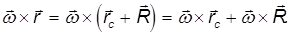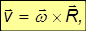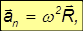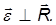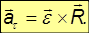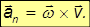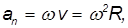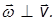в какую сторону вдоль оси вращения направлен вектор угловой скорости земли при ее суточном вращении
Вращательное движение и векторы
До этого такие параметры вращательного движения, как угловая скорость и угловое ускорение рассматривались, как скалярные величины. Но, на фактически, данные параметры являются векторами, т.к. обладают не только величиной, но и направлением.
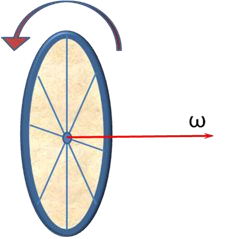
Например, вращающееся колесо автомобиля обладает не только угловой скоростью, но и угловым ускорением, при этом, направление угловой скорости колеса не совпадает с направлением линейной тангенциальной скорости, а перпендикулярно плоскости колеса (угловая скорость ω направлена вдоль оси вращающегося колеса).
Во вращающемся колесе единственной неподвижной точкой является его центр, по этой причине начало вектора угловой скорости располагают в центре окружности вращения.
Правило правой руки (определение направления вектора угловой скорости): если ладонью правой руки охватить ось вращения, таким образом, чтобы пальцы руки совпадали с направлением тангенциальной скорости, то, вытянутый большой палец будет указывать направление вектора угловой скорости ω.
Как определить направление углового ускорения
Угловое ускорение определяется формулой:
В векторной форме уравнение записывается следующим образом:
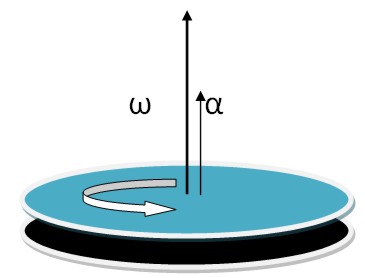
Таким образом, направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
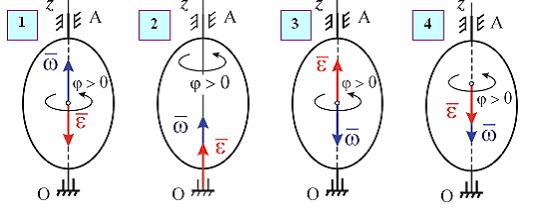
Направление векторов угловой скорости и углового ускорения совпадают (угловая скорость увеличивается).
Вектор углового ускорения направлен в противоположную сторону от вектора угловой скорости (угловая скорость уменьшается).
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
В какую сторону вдоль оси вращения направлен вектор угловой скорости земли при ее суточном вращении
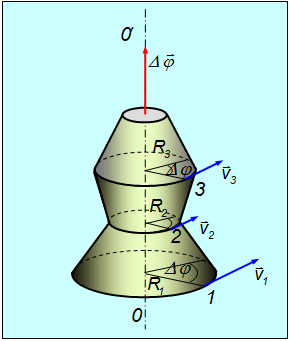
Движение тела как целого можно характеризовать только такими величинами, которые в данный момент времени для всех его точек одинаковы. Поэтому вращательное движение твердого тела характеризуют не линейными, а угловыми величинами: углом поворота Δφ, угловой скоростью ω и угловым ускорением ε.
Угловой скоростью вращения твердого тела называется вектор ω, численно равный первой производной от угла поворота по времени
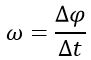
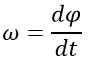
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение было видно происходящим против часовой стрелки. Также направление вектора угловой скорости можно определить по правилу буравчика.
Линейная скорость v произвольной точки М вращающегося тела определяется по формуле Эйлера
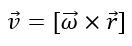
Угловым ускорением вращения твердого тела называется вектор ε, численно равный модулю второй производной от угла поворота по времени или первой производной от угловой скорости по времени
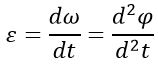
и направленный в ту же сторону, что и вектор угловой скорости, если движение ускоренной и в противоположную сторону от вектора угловой скорости, если движение замедленное. Если тело вращается равномерно, то ε = 0.
Вектор ускорения каждой точки тела, вращающегося вокруг неподвижной оси, можно разбить на две составляющие: нормальное (центростремительное) и тангенциальное. Вектор нормального ускорения направлен к оси вращения, а по модулю определяется по формуле
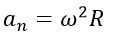
Вектор тангенциального ускорения направлен по касательной к окружности, а по модулю определяется по формуле
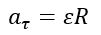
Отсюда модуль полного ускорения определяется по формуле
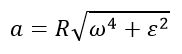
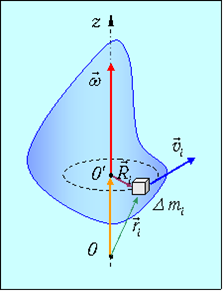
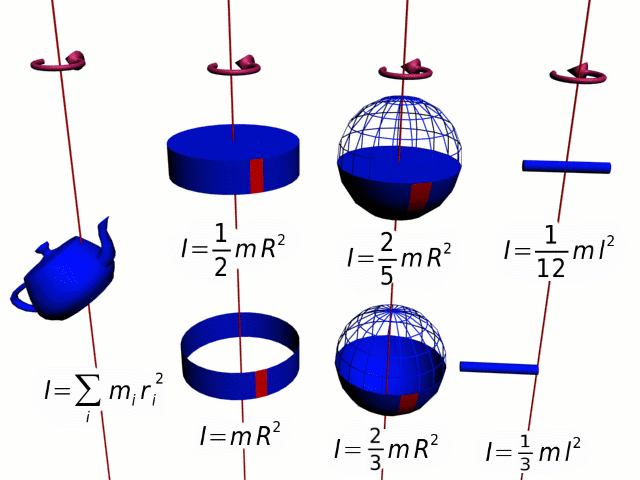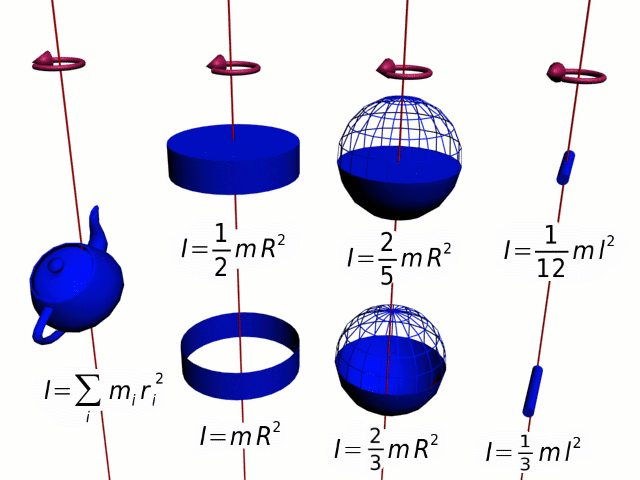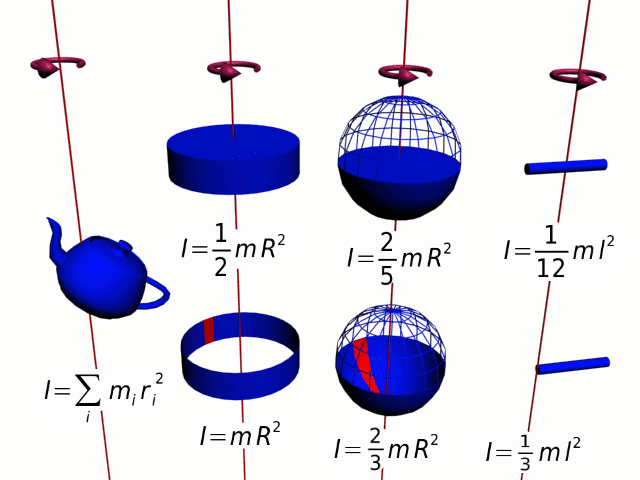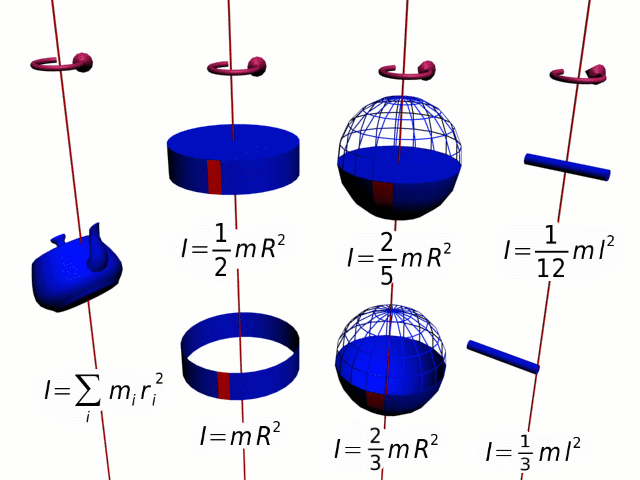
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через Ri, модули линейных скоростей – через vi. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина, зависящая от распределения масс вращающегося тела относительно оси вращения, называется моментом инерции тела относительно данной оси. Это величина, характеризующая инертность тела при вращательном движении.
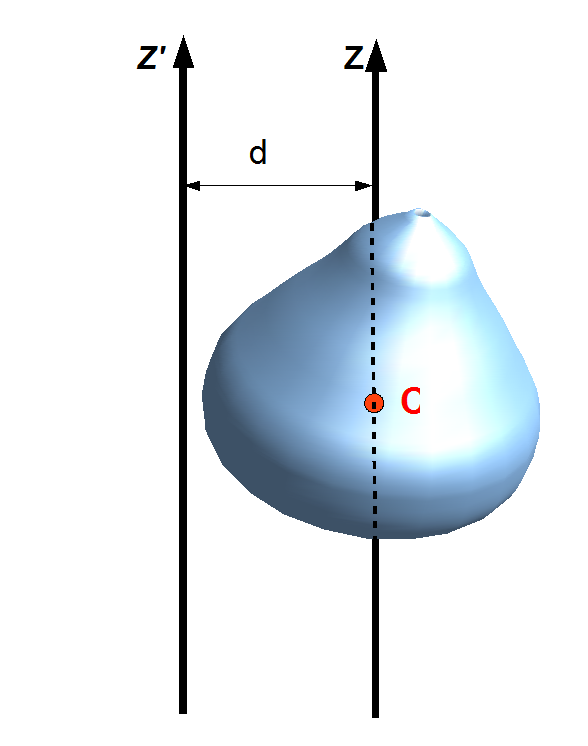
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой. Теорема Штейнера :
Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела :
Для описания вращательного движения вводятся величины, аналогичные тем, которыми характеризуют поступательное движение: момент силы аналогичен силе, момент инерции аналогичен массе.
Основной закон динамики вращательного движения (II закон Ньютона для вращательного движения) имеет вид:
где M – результирующий момент сил, действующий на тело, I – момент инерции тела, ε – угловое ускорение, полученное телом.
Закон сохранения момента импульса:
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется (момент импульса замкнутой системы остается неизменным):
L = const
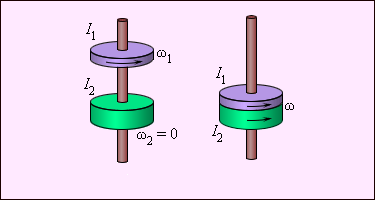
Пример: Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1ω1 = ( I 1 + I 2)ω
Аналогия величин и соотношений, характеризующих поступательное и вращательное движения
Магия тензорной алгебры: Часть 10 — Получаем вектор угловой скорости. Работаем над недочетами
Введение
Введение на этот раз будет «активным». Мы сразу начнем работать, и, пользуясь результатами предыдущих статей 6 и 9, получим псевдовектор угловой скорости твердого тела, выраженный через параметры конечного поворота.
Итак, путем долгих мучений вручную и, недолгих, но кропотливых преобразований в Maxima, мы пришли к тому, что антисимметричный тензор угловой скорости 2 ранга выглядит так
Мы говорили о том, что получить псевдовектор угловой скорости можно, свернув (1) с тензором Леви-Чивиты
Однако дальнейшее исследование показало, что формула (2) содержит ошибку, которая приводит к получению не совсем верного результата. Отгадка нашлась путем изучения литературы и дальнейшего самостоятельного осмысления результатов из статьи о свертке тензора Леви-Чивиты.
Приглашаю под кат всех, кому интересно, что получилось в итоге.
Не будем утруждать себя бумажной работой, используем Maxima, «натравив» её на пакетный файл
omega.mac
После доработки этого выражения вручную, получаем результат, очень похожий на правду
Только вот (3) ровно в два раза больше правды — если положить ось вращения неподвижной, то есть , мы получим
то есть угловая скорость направлена вдоль оси вращения, но в два раза больше производной от угла поворота. Как такое может быть? Такого быть не может, и неточность допущена в определении (2). Причины этой неточности, уточнение представлений об антисимметричных тензорах и псевдовекторах — цель данной статьи
1. Ещё раз о сопутствующем векторе антисимметричного тензора 2 ранга
Рассмотрим тензор угловой скорости (1). Так как он антисимметричный, то никто не мешает нам разложить его через самого себя
Результат (4) основан на антисимметричности тензора угловой скорости (), свойствах дельты Кронекера и её связи с тензором Леви-Чивиты, о чем подробно говорилось здесь.
А теперь внимание — введем вектор
и очевидно, что из этого вектора можно снова получить тензор (1)
в полном соответствии с (4). А теперь, проделаем с (6), то, что мы делали с (1) во введении — свернем с контравариантным тензором Леви-Чивиты
Вот и двойка нашлась — в действительности, сворачивая тензор угловой скорости с контравариантным тензором Леви-Чевиты мы получаем не одну, а две угловых скорости. Результат, полученный во введении является ошибочным, из-за того, что в пятой статье для получения сопутствующего вектора было приведено соотношение (2) и проигнорированы правила умножения и свертки тензора Леви-Чивиты. Как и в случае с метрическим тензором, для обратного преобразования достаточно умножить правую и левую часть выражения на обратный тензор. Но только метрический тензор при свертке с обратным ему по одной паре индексов дает дельту Кронекера, а вот тензор Леви-Чивиты при свертке по двум парам индексов дает ДВЕ дельты Кронекера. В этом и была причина ошибки и появления результата, в два раза превышающего истинный.
Для получения сопутствующего псевдовектора следует использовать соотношение (5). Тогда мы приходим к верному результату для угловой скорости
М-да, чтобы получить (8) пришлось потратить некоторое время. Поэтому в восьмой статье было уделено такое внимание свойствам тензора Леви-Чивиты. В пятую и шестую статью внесены соответствующие правки.
Допускать ошибки весьма досадно, учитывая ту аудиторию, что следит за моими публикациями. Однако, статьи данного цикла, кроме изложения тензорного исчисления и способов его применения к решению практических задач, иллюстрируют и процесс познания на моем конкретном примере. А процесс познания, как известно, состоит из многих итераций.
В конечном счете мы пришли к цели — получили выражение угловой скорости через параметры конечного поворота, причем для произвольных координат с невырожденной метрикой.
2. Почему же все-таки псевдовектор?
Итак, мы получили угловую скорость. Допустим, для простоты, ось вращения тела не меняет своего направления. Тогда формула (8) приходит к тривиальной форме
Вектор угловой скорости направлен вдоль оси вращения, в ту сторону, откуда вращение выглядит происходящим против часовой стрелки
Почему против часовой стрелки? Потому, что при изложении курса теоретической механики, физики и математики по-умолчанию используется правая система координат. В ней положительное направление поворота — против хода часовой стрелки.
Обратимся к (9). Положительное значение производной от угла поворота говорит нам, что угол возрастает со временем. А значит поворот происходит в положительном направлении, то есть, если 0″/>, тело вращается против часовой стрелки (орт оси вращения смотрит на нас). Скорость точки тела при вращении определяется формулой Эйлера
и здесь опять — вектор скорости будет направлен в ту сторону, откуда кратчайший поворот от угловой скорости к радиус-вектору выглядит происходящим в положительном направлении, то есть против часовой стрелки (рисунок 1).
Рис. 1. Вращение твердого тела — правая система координат
А теперь поменяем систему координат на левую (рисунок 2)
Рис. 2. Вращение твердого тела — левая система координат
Телу всё равно, в какой системе координат мы его рассматриваем. Оно вращается туда же, куда и вращалось. Но положительное направление отсчета углов поворота в новой системе — по часовой стрелке. А значит, с существующим направлением вращения тела угол его поворота уменьшается и 0″/>, значит вектор угловой скорости, согласно (9) меняет направление на противоположное.
Что же будет со скоростью точки тела? А ничего — теперь, в соответствии с (10), вектор будет направлен туда, откуда кратчайший поворот от угловой скорости к радиус-вектору будет выглядеть происходящим по часовой стрелке, ведь такое положительное направление выбрано в новой системе координат. А значит направление вектора скорости точки тела останется прежним.
Выходит, что при переходе от правой системы координат к левой и наоборот, то есть при смене ориентации базиса, вектор угловой скорости меняет направление. А значит, как целостный геометрический объект он не инвариантен к смене базиса. Такие векторы называют псевдовекторами. А ещё их называют аксиальными векторами, что подчеркивает факт — направление вектора определяется выбранным в данной системе координат положительным направлением поворота.
Вектор скорости, напротив, не меняет направления при смене ориентации базиса и называется истинным или полярным вектором.
Результат векторного произведения истинных векторов — это аксиальный вектор. Но почему (10) дает истинный вектор? А потому, что один из аргументов вектор аксиальный, и смена его направления при переходе к левой системе координат нивелирует изменение направление векторного произведения. Таким образом, векторное произведение псевдовектора на истинный вектор дает на выходе истинный вектор.
В этом смысле вектор угловой скорости величина несколько неудобная. Поэтому, при выводе тензорных соотношений механики твердого тела лучше опираться на тензор угловой скорости, который инвариантен относительно произвольных преобразований системы координат.
3. Немного практики — вывод кинематических уравнений Эйлера из тензора угловой скорости
Чтобы читатель не заскучал от громоздких формул и понял практическую ценность полученных соотношений, приведу пример того, как можно получить выражение компонент угловой скорости через произвольные параметры поворота тела. Например через углы Эйлера.
Будем работать в декартовой правой системе координат. Углы Эйлера позволяют задать произвольную ориентацию твердого тела в пространстве, так, как показано на рисунке 3.
Рис. 3. Углы Эйлера — последовательный поворот связанной системы координат вокруг осей z,x,z
Произвольная ориентация тела может быть получена путем трех последовательных поворотов — вокруг оси z на угол (угол нутации), затем, вокруг нового положения оси x на угол
(угол прецессии), и, вокруг нового положения оси z на угол
— угол собственного вращения.
Значит, матрица поворота, в декартовых координатах будет выглядеть как композиция линейных преобразований поворота вокруг осей z, x, z
Теперь применим к (11) одно их выражений для получения тензора поворота
получаем матрицу тензора поворота
Из (12) легко получить компоненты угловой скорости в системе координат, связанной с телом
Искушенный в механике читатель непременно узнает в (13) — (15) кинематические уравнения Эйлера, связывающие вектор угловой скорости с параметрами поворота тела, в качестве которых выбраны углы Эйлера.
Похожим образом можно связать угловую скорость с любыми параметрами поворота. Мы проделали все преобразования для получение формулы (8) в общем виде, связав угловую скорость с параметрами конечного поворота. Но, ни представление (8), ни представление (13) — (15) неудобны для динамического анализа движения твердого тела, так как перечисленные формулы подвержены вырождению при определенных значениях параметров. В дальнейшем мы используем (8) чтобы перейти к угловой скорости, выраженной через компоненты кватерниона, не подверженные вырождению. А данный пример носит проверочный и иллюстративный характер.
Заключение
Данная заметка большей частью — работа над ошибками и неточностями, допущенными в предыдущих публикациях. Но результат достигнут — мы получили определение вектора угловой скорости тела через параметры конечного поворота и наглядно показали, что угловая скорость — псевдовектор.
2.8. Вращение абсолютно твердого тела
Рассмотрим кинематику движения протяженного тела, размерами которого в условиях рассматриваемой задачи пренебречь нельзя. Тело будем считать недеформируемым, другими словами, — абсолютно твердым.
Движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе, называется поступательным.
Под прямой «жестко связанной с телом» понимается такая прямая, расстояние от любой точки которой до любой точки тела остается постоянным при его движении.
Поступательное движение абсолютно твердого тела можно охарактеризовать движением какой-либо точки этого тела, так как при поступательном движении все точки тела движутся с одними и теми же скоростями и ускорениями, а траектории их движения конгруэнтны. Определив движение какой-нибудь из точек твердого тела, мы вместе с тем определим движение всех остальных его точек. Поэтому при описании поступательного движения не возникает новых проблем по сравнению с кинематикой материальной точки. Пример поступательного движения показан на рис. 2.20.
Рис.2.20. Поступательное движение тела
Пример поступательного движения показан на следующем рисунке:
Рис.2.21. Плоское движение тела
Другой важный частный случай движения твердого тела — это движение, при котором две точки тела остаются неподвижными.
Движение, при котором две точки тела остаются неподвижными, называется вращением вокруг неподвижной оси.
Прямая, соединяющая эти точки, также неподвижна и называется осью вращения.
Рис.2.22. Вращение твердого тела
При таком движении все точки тела движутся по окружностям, расположенным в плоскостях, перпендикулярных оси вращения. Центры окружностей лежат на оси вращения. При этом ось вращения может находиться и вне тела.
Видео 2.4. Поступательное и вращательное движения.
Угловая скорость, угловое ускорение. При вращении тела вокруг какой-либо оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее, можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют иные (по сравнению с материальной точкой) кинематические характеристики движения — угол поворота 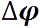
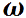
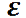
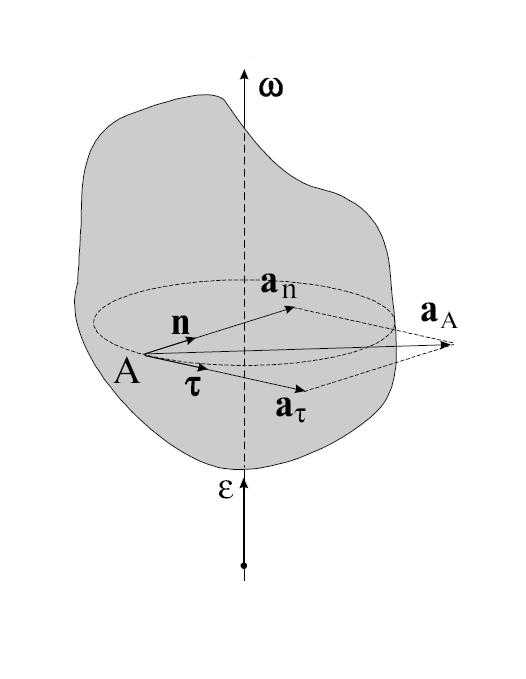
Рис. 2.23. Вектора ускорения точки, движущейся по окружности
Роль перемещения 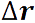
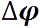
Рис. 2.24. Вращение абсолютно твердого тела вокруг неподвижной оси
Модуль вектора поворота равен величине угла поворота 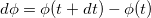
Направлен вектор бесконечно малого поворота по оси вращения в сторону движения правого винта (буравчика), вращаемого в том же направлении, что и тело.
Видео 2.5. Конечные угловые перемещения — не векторы, так как не складываются по правилу параллелограмма. Бесконечно малые угловые перемещения – векторы.
Векторы, направления которых связаны с правилом буравчика, называют аксиальными (от англ. axis — ось) в отличие от полярных. векторов, которыми мы пользовались ранее. Полярными векторами являются, например, радиус-вектор, вектор скорости, вектор ускорения и вектор силы. Аксиальные векторы называют также псевдовекторами, так как они отличаются от истинных (полярных) векторов своим поведением при операции отражения в зеркале (инверсии или, что то же самое, переходе от правой системы координат к левой). Можно показать (это будет сделано позже), что сложение векторов бесконечно малых поворотов происходит так же как и сложение истинных векторов, то есть по правилу параллелограмма (треугольника). Поэтому, если операция отражения в зеркале не рассматривается, то отличие псевдовекторов от истинных векторов никак не проявляет себя и обходиться с ними можно и нужно как с обычными (истинными) векторами.
Отношение вектора бесконечно малого поворота ко времени, за которое этот поворот имел место
называется угловой скоростью вращения.
Видео 2.6. Стробоскопический эффект и его использование для дистанционного измерения угловой скорости вращения.
Угловая скорость 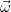
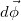
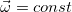
Период вращения — это время, за которое тело совершает один оборот (поворот на угол 2π) вокруг оси вращения.
Слова «достаточного постоянства» означают, очевидно, что за период (время одного оборота) модуль угловой скорости меняется несущественно.
Часто используют также число оборотов в единицу времени
При этом в технических приложениях (прежде всего, всякого рода двигатели) в качестве единицы времени общепринято брать не секунду, а минуту. То есть угловая скорость вращения 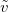

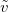
Направление вектора угловой скорости показано на рис. 2.25.
Рис. 2.25. Направление вектора угловой скорости
По аналогии с линейным ускорением вводится угловое ускорение 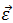
Угловое ускорение 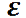
При вращении вокруг неподвижной оси, в более общем случае при вращении вокруг оси, которая остается параллельной самой себе, вектор угловой скорости также направлен параллельно оси вращения. При возрастании величины угловой скорости |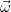
Связь угловых и линейных скоростей и ускорений. Каждая из точек вращающегося тела движется с определенной линейной скоростью 
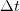
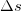
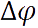
Переходя к пределу 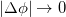
Напомним, здесь R — расстояние от рассматриваемой точки тела до оси вращения.
Рис. 2.27. Направление движения искр при заточке инструментов.
Так как нормальное ускорение равно
то с учетом соотношения для угловой и линейной скорости получаем
Нормальное ускорение точек вращающегося твердого тела часто называют центростремительным ускорением.
Дифференцируя по времени выражение для 
где 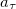
Таким образом, как тангенциальное, так и нормальное ускорения растут линейно с ростом радиуса R — расстояния от оси вращения. Полное ускорение также линейно зависит от R :
Пример. Найдем линейную скорость 
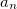
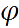
Средний радиус Земли
Расстояние до оси вращения на широте 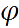
Отсюда находим линейную скорость
и центростремительное ускорение
На экваторе 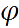
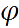
На широте Москвы cos 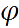
Мы видим, что влияние вращения Земли не столь велико: отношение центростремительного ускорения на экваторе к ускорению свободного падения равно
Тем не менее, как мы увидим в дальнейшем, эффекты вращения Земли вполне наблюдаемы.
Связь между векторами линейной и угловой скорости. Полученные выше соотношения между угловой и линейной скоростью записаны для модулей векторов 

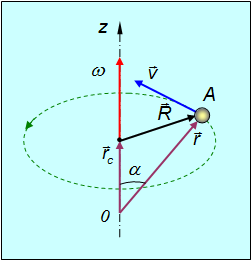
Пусть 0z — ось вращения абсолютно твердого тела (рис. 2.28).
Рис. 2.28. Связь между векторами линейной и угловой скорости
Точка А вращается по окружности радиусом R. R — расстояние от оси вращения до рассматриваемой точки тела. Примем точку 0 за начало координат. Тогда
то по определению векторного произведения, для всех точек тела
Здесь 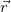
Но, с другой стороны
Первое слагаемое равно нулю, так как векторное произведение коллинеарных векторов равно нулю. Следовательно,
где вектор R перпендикулярен оси вращения и направлен от нее, а его модуль равен радиусу окружности, по которой движется материальная точка и начинается этот вектор в центре этой окружности.
Рис. 2.29. К определению мгновенной оси вращения
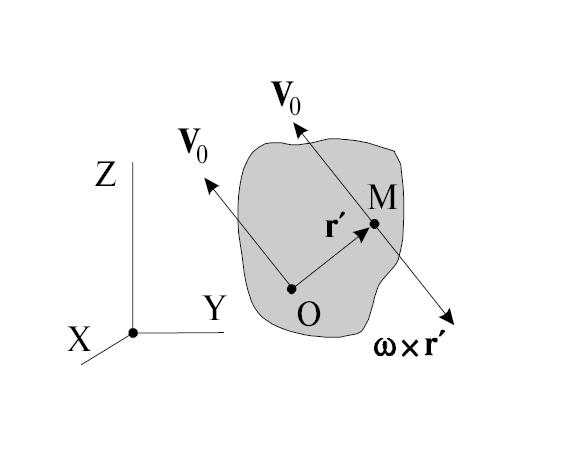
Нормальное (центростремительное) ускорение также можно записать в векторной форме:
причем знак «–» показывает, что оно направлено к оси вращения. Дифференцируя соотношение для линейной и угловой скорости по времени, находим для полного ускорения выражение
Первое слагаемое направлено по касательной к траектории точки на вращающемся теле и его модуль равен 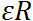
Сравнивая с выражением для тангенциального ускорения, приходим к выводу, что это — вектор тангенциального ускорения
Следовательно, второе слагаемое представляет собой нормальное ускорение этой же точки:
Действительно, оно направлено вдоль радиуса R к оси вращения и его модуль равен
Поэтому данное соотношение для нормального ускорения является другой формой записи ранее полученной формулы.