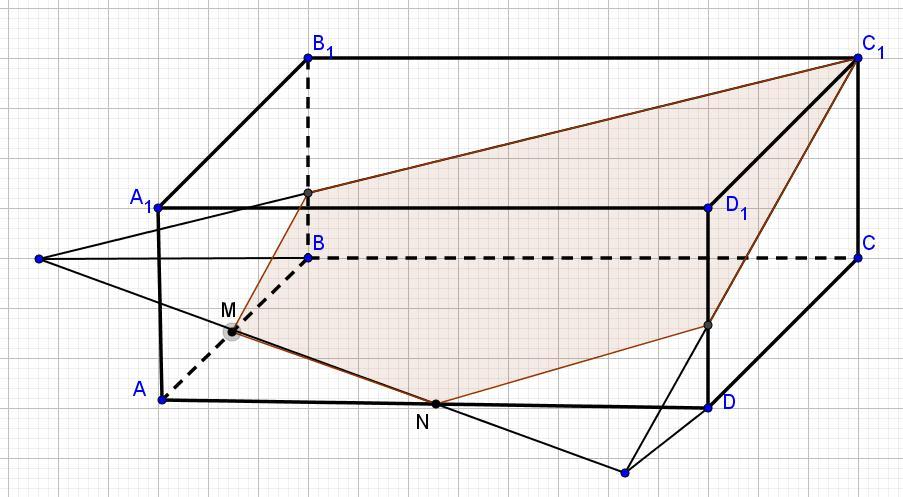
в кубе abcda1b1c1d1 проведено сечение через середины ребер aa1 и cc1 и вершину b каким
В кубе ABCDA1B1C1D1 проведено сечение через середины рёбер AB и AD и вершину C1. Каким многоугольником является это сечение? Сде
Сечением является пятиугольник.
Равные стороны у него MKC1 и NPC1.
На прилагаемом рисунке точка К на ребре ВВ1, точка Р на ребре ДД1.
2)Сумма углов в четырехугольнике 360°.
360/10=36° приходится на одну часть.
Наименьший угол 36°.
Δ АВК равнобедренный, так как углы при основании равны из условия.
АВ=ВК=6 см.ВС=6+10=16 см.
В сечении, параллельном одной из граней, тоже будет равносторонний треугольник, подобный тому, которому сечение параллельно. В данной задаче в соответствии с заданием коэффициент подобия равен: к = (1/2).
Периметр сечения равен: Р1 = Р*к = 18 * (1/2) = 9 см.
Площадь сечения равна: S1 = S*к² = (9√3)*(1/2)² = 9√3/4.
В кубе abcda1b1c1d1 проведено сечение через середины ребер aa1 и cc1 и вершину b каким
Загрузка решений доступна для зарегистрировавшихся пользователей
В пирамиде SABC в основании лежит правильный треугольник ABC со стороной
Точка O — основание высоты пирамиды, проведённой из вершины S.
а) Докажите, что точка O лежит вне треугольника ABC.
б) Найдите объём четырёхугольной пирамиды SABCO.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 8. Точка L — середина ребра SC. Тангенс угла между прямыми BL и SA равен
а) Пусть O — центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.
Загрузка решений доступна для зарегистрировавшихся пользователей
В треугольной пирамиде ABCD двугранные углы при рёбрах AD и BC равны. AB = BD = DC = AC = 5.
а) Докажите, что AD = BC.
б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60°.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной треугольной призме ABCA1B1C1 все рёбра равны 6. На рёбрах AA1 и CC1 отмечены точки M и N соответственно, причём AM = 2, CN = 1.
а) Докажите, что плоскость MNB1 разбивает призму на два многогранника, объёмы которых равны.
б) Найдите объём тетраэдра MNBB1.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной треугольной призме ABCA1B1C1 все рёбра равны 8. На рёбрах AA1 и CC1 отмечены точки M и N соответственно, причём AM = 3, CN = 1.
а) Докажите, что плоскость MNB1 разбивает призму на два многогранника, объёмы которых равны.
б) Найдите объём тетраэдра MNBB1.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана правильная треугольная призма ABCA1B1C1 со стороной основания 12 и высотой 3. Точка K — середина BC, точка L лежит на стороне A1B1 так, что В1L = 5. Точка М — середина A1C1. Через точки K и L проведена плоскость таким образом, что она параллельна прямой AC.
а) Докажите, что указанная выше плоскость перпендикулярна прямой MB.
б) Найдите объем пирамиды с вершиной в точке В, у которой основанием является сечение призмы плоскостью.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L — середина ребра SC. Тангенс угла между прямыми BL и SA равен
а) Пусть O — центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.
Загрузка решений доступна для зарегистрировавшихся пользователей
а) Докажите, что PBDC1 — правильный тетраэдр.
б) Найдите длину отрезка AP.
Загрузка решений доступна для зарегистрировавшихся пользователей
На ребрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём Точки P и Q — середины сторон DA и DC соответственно.
а) Доказать, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объемов многогранников, на которые плоскость PQM разбивает пирамиду.
Загрузка решений доступна для зарегистрировавшихся пользователей
На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM = CN : NB = 1 : 2. Точки P и Q — середины ребер DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Загрузка решений доступна для зарегистрировавшихся пользователей
На ребрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём Точки P и Q — середины сторон DA и DC соответственно.
а) Доказать, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объемов многогранников, на которые плоскость PQM разбивает пирамиду.
Загрузка решений доступна для зарегистрировавшихся пользователей
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 6, BC = 3.
Загрузка решений доступна для зарегистрировавшихся пользователей
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 7, BC = 8.
Загрузка решений доступна для зарегистрировавшихся пользователей
В треугольной пирамиде SABC известны боковые рёбра: SA = SB =13, Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 12.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Загрузка решений доступна для зарегистрировавшихся пользователей
В треугольной пирамиде SABC известны боковые рёбра: Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Загрузка решений доступна для зарегистрировавшихся пользователей
а) Докажите, что B1KLM — правильная пирамида.
Загрузка решений доступна для зарегистрировавшихся пользователей
Основанием прямой треугольной призмы является прямоугольный треугольник ABC с прямым углом C. Диагонали боковых граней
и
равны 15 и 9 соответственно,
а) Докажите, что треугольник прямоугольный.
б) Найдите объём пирамиды
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана правильная четырёхугольная пирамида SABCD с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q середина ребра BC.
а) Докажите, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.
а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.
б) Найдите объём PKBC, если AB = BC = CD = 3, а PK = 8.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90°, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.
а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.
б) Найдите объём PKBC, если AB = BC = CD = 2, а PK = 12.
Загрузка решений доступна для зарегистрировавшихся пользователей
В треугольной пирамиде PABC с основанием ABC известно, что AB = 13, PB = 15, Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Загрузка решений доступна для зарегистрировавшихся пользователей
В треугольной пирамиде PABC с основанием ABC известно, что AB = 17, PB = 10, Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Загрузка решений доступна для зарегистрировавшихся пользователей
а) Докажите, что прямые A1C и BD перпендикулярны.
б) Найдите объем призмы, если A1C = BD = 2.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна боковому ребру SA. Медианы треугольника SBC пересекаются в точке M.
а) Докажите, что
б) Точка N — середина AM. Найдите SN, если
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана правильная треугольная пирамида SABC, M — середина AB, N — середина CS.
а) Докажите, что проекции отрезков MN и AS на плоскость ABC равны.
б) Найдите объем пирамиды SABC, если AS = 8, MN = 5.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4.
а) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды.
б) Найдите объем пирамиды CDKM.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 7, а боковое ребро SA = 10. Точка M лежит на ребре BC, причем BM = 4, точка K лежит на ребре SC, причем SK = 7.
а) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды.
б) Найдите объем пирамиды CDKM.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана правильная треугольная призма ABCA1B1C1 в которой AB = 6 и AA1 = 3. Точки O и O1 являются центрами окружностей, описанных около треугольников ABC и A1B1C1 cответственно. На ребре CC1 отмечена точка M такая что CM = 1.
а) Докажите, что прямая OO1 содержит точку пересечения медиан треугольника треугольника ABM.
б) Найдите объем пирамиды ABMC1.
Загрузка решений доступна для зарегистрировавшихся пользователей
Дана правильная треугольная призма ABCA1B1C1, в которой AB = 1 и AA1 = 3. Точки O и O1 являются центрами окружностей, описанных около треугольников ABC и A1B1C1 cответственно. На ребре CC1 отмечена точка M такая что CM = 2.
а) Докажите, что прямая OO1 содержит точку пересечения медиан треугольника треугольника ABM.
б) Найдите объем пирамиды ABMC1.
Загрузка решений доступна для зарегистрировавшихся пользователей
В правильной четырёхугольной пирамиде SABCD сторона основания AB = 8, а боковое ребро SA = 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = 2, SK = 1.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
Загрузка решений доступна для зарегистрировавшихся пользователей
В кубе abcda1b1c1d1 проведено сечение через середины ребер aa1 и cc1 и вершину b каким
В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
а) Проведём через точку N прямую, параллельную прямой AB, до пересечения с прямой B1C1 в точке K. Трапеция ABKN — искомое сечение.
б) Имеем A1N= 3, так как точка N — середина ребра A1C1. Значит, Аналогично BK = 5.
Далее NK = 3, как средняя линия треугольника A1B1C1. Следовательно, искомый периметр сечения равен 6 + 5 + 5 + 3 = 19.
В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
а) В плоскости ABP через точку K проведем прямую, параллельную прямой PB до пересечения ее с прямой AB в точке L — середине AB. В основании ABCD через точку L проведем прямую, параллельную прямой BC до пересечения ее с ребром СD в точке M — его середине. По признаку параллельности прямой и плоскости плоскость KLM параллельна прямым PB и BC. Прямая LM параллельна прямой AD, следовательно, она параллельна плоскости APD, а, значит плоскость KLM пересекает плоскость APD по прямой, параллельной LM и пересекает ребро PD в его середине N.
Таким образом, искомое сечение ― трапеция KLMN.
б) Отрезки KL и MN равны, как средние линии равных правильных треугольников ABP и DCP, а отрезок LM ― средняя линия квадрата ABCD, следовательно, построенное сечение ― равнобедренная трапеция, в которой LM = 4, KL = KN = MN = 2. Проведем высоту KF этой трапеции. Тогда и из прямоугольного треугольника KLF находим
Окончательно получаем
Ответ:
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — середина ребра B1C1. Известно, что AD = 12, AA1 = 14.
а) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4 : 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
а) Проведём отрезок и в плоскости грани
проведём через точку
прямую, параллельную
Эта прямая пересечёт ребро
в точке
Точка
лежит в плоскости
Треугольники
и
подобны, как треугольники с параллельными сторонами, следовательно,
Таким образом, Тогда
и
б) Четырёхугольник — сечение параллелепипеда плоскостью
Поскольку стороны
и
параллельны, но не равны. Четырёхугольник
— трапеция. Продолжим боковые стороны
и
до пересечения в точке
Точка
— середина
поэтому отрезок
— средняя линия треугольника
Из равенства треугольников
и
получаем
откуда
то есть трапеция
— равнобедренная.
Найдём стороны трапеции:
Высота равнобедренной трапеции
Тогда