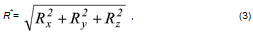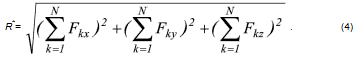в многоугольнике сил какой вектор изображает равнодействующую силу

Равнодействующая сходящихся сил

Равнодействующая сходящихся сил

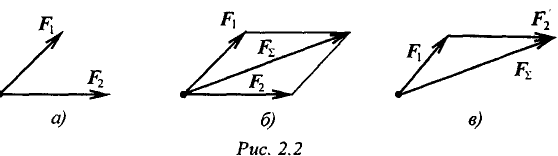
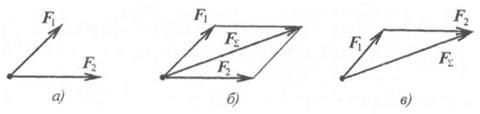
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).

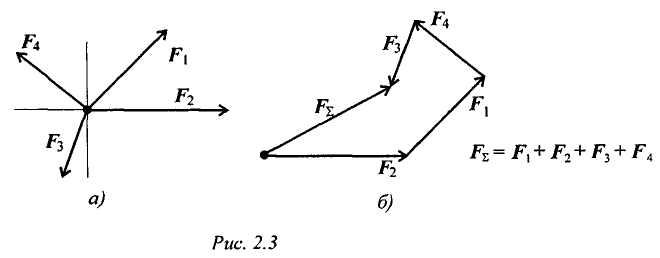
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.

Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

iSopromat.ru

Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Система сходящихся сил

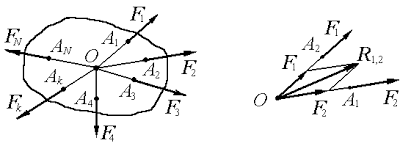
Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * _1,2 и силы F₃, тогда

Для системы N сил окончательно будем иметь

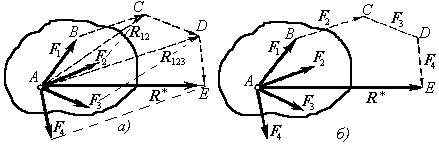
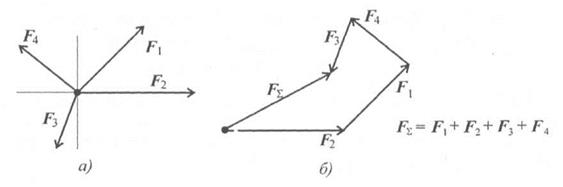
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

Тогда величина равнодействующей определится следующей формулой:

Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

КАКОЙ ВЕКТОР В МНОГОУГОЛЬНИКЕ СИЛ ПОКАЗЫВАЕТ РАВНОДЕЙСТВУЮЩУЮ СИЛУ

А)

В)

С)

D)

Е)

ЛЕММА ПУАНСО – СТР. 17 ВЕРЕИНА

А)два материальных тела действуют друг на друга с силами, равными по величине и противоположно направленными. Такая система сил не является уравновешенной т.к. силы приложены к разным телам

В) две силы, действующие на свободное (твердое) тело, находятся в равновесии тогда и только тогда, когда они равны по модулю и направлены вдоль одной прямой в противоположные стороны

С) произвольную плоскую систему сил заменить одной силой, равной геометрической сумме всех сил, приложенных в произвольной выбранном центре и моментом, равным алгебраической сумме моментов присоединенных пар.

D) два тела действуют друг на друга с силами, равными по величине и противоположно направленными

Е) если деформируемое тело в равновесии под действием системы сил, то равновесие не нарушится, если тела станут абсолютно твёрдыми

КАКОЙ ВЕКТОР В МНОГОУГОЛЬНИКЕ СИЛ ПОКАЗЫВАЕТ РАВНОДЕЙСТВУЮЩУЮ СИЛУ

А)

В)

С)

D)

Е)

ОСНОВНАЯ ЗАДАЧА СТАТИКИ

А)определить условия равновесия сил

С)определить реакции опор от действующих сил

D) найти равнодействующую силу

Е) определить абсолютно твердое тело

ПОЧЕМУ СИСТЕМА НЕ ЯВЛЯЕТСЯ УРАВНОВЕШЕННОЙ, ЕСЛИ ДВА МАТЕРИАЛЬНЫХ ТЕЛА ДЕЙСТВУЮТ ДРУГ НА ДРУГА С РАВНЫМИ СИЛАМИ СИЛА И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫМИ

А) силы действуют на разное тело

В) они направлены в противоположные стороны

С) модули сил не равны между собой

D) они направлены по одной прямой

Е) направлены в одну сторону

КАКОЙ ВИД СВЯЗИ НА ЧЕРТЕЖЕ?

А) гладкая поверхность

С) подвижный шарнир

D) жесткая защемление

Е) гладкая опора

УСЛОВИЯ РАВНОВЕСИЯ ДЛЯ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ

Источник

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n — число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

Источник

Равнодействующая сходящихся сил

Равнодействующую двух пересекающихся сил можно опреде­лить с помощью параллелограмма или треугольника сил (4-я ак­сиома) (рис. 1.13).

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 1.13). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

При графическом способе определения равнодействующей век­торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.

З а м е ч а н и е. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствую­щим векторам сил.

Порядок построения многоугольника сил

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора со­впадал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил

При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

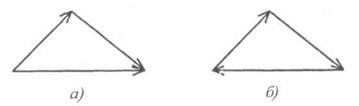
Сравните два треугольника сил (рис. 2.4) и сделайте вывод количестве сил, входящих в каждую систему.

Р е к о м е н д а ц и я. Обратить внимание на направление векторов.

Решение задач на равновесие геометрическим способом:

Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).

Порядок решения задач:

1. Определить возможное направление реакция связей.

2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы – слагаемые направлены в одну сторону по обходу контура.)

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения решения рекомендуется определить их величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

Дата добавления: 2015-08-08 ; просмотров: 3310 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник