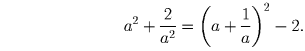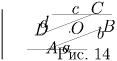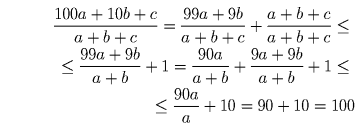в отряде 27 туристов какое наименьшее количество лодок надо взять на лодочной станции чтобы всем

Самостоятельная работа. 5 класс. «Деление с остатком».

Ищем педагогов в команду «Инфоурок»

Самостоятельная работа. 5 класс. «Деление с остатком».

Вариант №1.

В отряде 27 туристов. Какое наименьшее количество лодок надо взять на лодочной станции, чтобы всем одновременно переправиться через реку, если вместимость лодки 4 человека?

Бабушка сварила 43л вишневого варенья. Какое наименьшее количество трехлитровых банок нужно взять, чтобы разлить все варенье?

Необходимо разлить в банки 17л кваса. Какое наименьшее количество двухлитровых банок надо взять, чтобы разлить весь квас?

Вариант № 2.

В загородный лагерь необходимо вывезти 150 человек. Какое наименьшее количество автобусов надо заказать, если вместимость автобуса 42 пассажира?

Антон живет в доме с одним подъездом, в квартире № 49. На каком этаже живет Антон, если на каждом этаже расположено по 8 квартир?

На туристический слет приехали 112 участников. Какое наименьшее количество шестиместных палаток должны заготовить организаторы, чтобы разместить всех участников?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДВ-163833

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Школьников не планируют переводить на удаленку после каникул

Время чтения: 1 минута

В Москве стартует онлайн-чемпионат для школьников Soft Skills — 2035

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

55 российских школ остаются на карантине по коронавирусу

Время чтения: 0 минут

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Время чтения: 1 минута

Средняя зарплата учителей в Москве достигла 122 тыс. рублей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Группа из 28 туристов отправилась в лодочный поход?

Группа из 28 туристов отправилась в лодочный поход.

6 * 2 = 12туристов вместились на 2 шестиместных лодках.

Решите пожалуйста Для путешествия по реке 76 туристов заготовили лодки и ялики?

Решите пожалуйста Для путешествия по реке 76 туристов заготовили лодки и ялики.

Четырёх местных лодок было 7.

Сколько 6 местных я ликов приготовили для туристов?

Всего в эти лодки может поместиться 14 человек.

46 туристов рассадили в 10 лодок, лодки 6 и 4 местные, свободных мест не осталось, сколько лодок 6 и сколько лодок 4 местных поличилось решить математически?

46 туристов рассадили в 10 лодок, лодки 6 и 4 местные, свободных мест не осталось, сколько лодок 6 и сколько лодок 4 местных поличилось решить математически.

Группа в составе 47 человек собирается с турбазы в поход по реке на лодках?

Группа в составе 47 человек собирается с турбазы в поход по реке на лодках.

Какое наименьшее число четырёх местных лодок надо заказать для такой группы.

Помогите пожалуйста?

В поход отправилось 48 туристов на 10 лодках.

Сколько лодок каждого вида?

Помогите пожалуйста решить задачу : На лодочной станции было 150 лодок?

Помогите пожалуйста решить задачу : На лодочной станции было 150 лодок.

Трёхместные лодки составляет 14℅ всех лодок и ⅞ числа пятиместных лодок.

Сколько четырёх местных лодок было на станции?

Люди помогить решить очень надо!

Составьте систему линейных уравнений?

Составьте систему линейных уравнений.

Группа из 31 туриста переплыла на 7 лодках на другой берег.

Путешествия по реке 76 туристов заготовили лодки и ялики четырехместных лодок было 7 сколько было 6 местных яликов приготовили для туристов?

Путешествия по реке 76 туристов заготовили лодки и ялики четырехместных лодок было 7 сколько было 6 местных яликов приготовили для туристов.

Источник

Олимпиада по математике школьный этап 2021 ВОШ задания и ответы для 4-11 класса

ПОДЕЛИТЬСЯ

Задания и ответы школьного этапа 2021 олимпиады по математике для 4-11 класса всероссийской олимпиады школьников 2021-2022 учебного года, официальная дата проведения олимпиады в Омске: 06.10.2021 (6 октября 2021 года)

Задания и ответы для 4 класса: скачать

Задания и ответы для 5 класса: скачать

Задания и ответы для 6 класса: скачать

Задания и ответы для 7 класса: скачать

Задания и ответы для 8 класса: скачать

Задания и ответы для 9 класса: скачать

Задания и ответы для 10 класса: скачать

Задания и ответы для 11 класса: скачать

Интересные задания и ответы олимпиады:

1)Ваня представил число 100 в виде суммы 14 слагаемых, имеющих одинаковую сумму цифр: 100=20+20+20+20+2+2+2+2+2+2+2+2+2+2 (сумма цифр числа 20 равна 2+0=2). Вася смог представить число 100 в виде суммы 11 слагаемых, имеющих одинаковую сумму цифр. Как он это сделал? Достаточно привести один пример такого представления.

Ответ: 100=50+5+5+5+5+5+5+5+5+5+5.

2)Вера, накопив 200 рублей, хотела купить пенал, но этих денег ей не хватило. Через несколько дней пенал уценили, и он стал стоить в два раза меньше. Теперь Вера смогла его купить и даже получила сдачу 15 рублей. Сколько стоил пенал первоначально? Ответ нужно подтвердить вычислениями и объяснениями.

Ответ: 370 р.

3)Фермер огородил снаружи участок земли и разделил его на квадратики со стороной 3 м. В пяти квадратиках он разместил гусятники (обозначены «Г»), а в других пяти – будки со сторожевыми собаками (обозначены «С»). Но гуси нападают на собак, а собаки могут загрызть гусей. Помогите фермеру построить по линиям сетки дополнительные заборы общей длины 30 м, чтобы защитить собак от гусей и гусей от собак.

Ответ: например, так, как на рисунке справа.

4)По кругу стоят 10 сорочат. Мама–сорока кормит их кашей: первому – 1 ложку, второму – 2 ложки, следующему – 1, потом – 2 и так далее. Всего она раздала 55 ложек каши, и на этом каша закончилась. Сколько сорочат получили ровно 4 ложки каши? Ответ нужно обосновать.

Ответ: 4 птенца

5)Никита записал два нечётных числа, а потом заменил в них разные цифры разными буквами, а одинаковые – одинаковыми. У Никиты получились два слова: УЧИТЕЛЯ и МЕЧТАТЕЛИ. Известно, что произведение цифр числа УЧИТЕЛЯ не равно нулю, а произведение цифр числа МЕЧТАТЕЛИ равно нулю. Чётной или нечётной будет сумма Я+И+МЕЧТА? Ответ нужно обосновать.

Ответ: чётная

6)В семье Веснушкиных три человека, и у каждого на лице в два раза больше веснушек, чем ему лет. Васе сейчас 11 лет. Васина мама младше Васиного папы на 3 года, и у неё на лице 66 веснушек. Сколько веснушек на лице у всех троих вместе? Ответ нужно подтвердить вычислениями и объяснениями.

Ответ: 160 веснушек.

7)Найдите какое-нибудь решение неравенства М Ответ: например, М=1, А=3, Т=2, Е=4, И=5, К=9, т.е. 1

8)Маша попросила встать 30 одноклассников по кругу и стала раздавать им шоколадные конфеты. Первому дала 1 конфету, второму – 2 конфеты, следующему – снова 1 конфету, потом – 2 конфеты и так далее. Всего она раздала 55 конфет, и на этом конфеты закончилась. Сколько Машиных одноклассников получили ровно 2 конфеты? Ответ нужно обосновать

Ответ: 16 человек

9)На рисунке слева изображена фигура на клетчатой бумаге. Сторона каждой клетки равна 1 см. Разрежьте данную фигуру по линиям сетки на фигурки, удовлетворяющие всем четырём условиям: 1) площадь каждой равна 5 см2 ; 2) периметр каждой равен 12 см; 3) все фигурки должны быть различными, т.е. не совпадать при наложении; 4) в каждой должен быть ровно один серый квадратик. Достаточно привести один вариант разрезания.

Ответ: например, как на рисунке ниже.

10)Винни-Пух, Пончик и Карлсон приняли участие в турнире обжор. По результатам трёх туров судья заполнил таблицу, где указал, сколько пирогов в каждом туре съел каждый участник. Оказалось, что все числа в таблице различны. Ночью каждый из участников увеличил только один из своих результатов в таблице на 1. Утром все увидели следующую таблицу.

Ответ: см. файл выше

11)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.

Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.

12)Мальвина написала на доске выражение М+А = Т+Е = М+А+Т = И+К+А и попросила Буратино заменить все буквы цифрами так, чтобы равенства оказались верными. Причем разные буквы нужно заменять разными цифрами, а одинаковые буквы ‒ одинаковыми цифрами. Помогите Буратино справиться с задачей. Достаточно привести хотя бы один пример.

Ответ: пусть М=5, А=2, Т=0, Е=7, И=1, К=4. Тогда получим верные равенства: 5+2=0+7=5+2+0=1+4+2.

13)Семи детям раздали 55 конфет. После этого первыйсказал, что по крайней мере 1 конфета у него имеется. «А у меня ровно на две больше!» — сказал второй. «А у меня ровно на две больше, чем у тебя!» — сказал третийвторому, затем такую же фразу произнес четвертый— третьему, пятый – четвертому, шестой— пятому. А седьмой заявил: «А у меня конфет больше всех!». Сколько конфет получил седьмой ребенок? Найдите все варианты и докажите, что других нет.

Ответ: 13 или 19

14)У Алисы есть три деревянных кубика. Длина ребра меньшего кубика равна 1 дм, среднего — 2 дм, большего — 3 дм. На покраску меньшего кубика ей потребовалось на 120 г краски меньше, чем на покраску среднего кубика. Сколько граммов краски ей потребуется на покраску большего кубика?

Ответ: 360 г.

15)Чтобы насытиться, голодному кролику нужно съесть ровно три каких-нибудь различных овоща. Какое наибольшее количество голодных кроликов можно накормить досыта, если в запасах имеется 5 кукуруз, 8 огурцов, 11 морковок и 17 перцев? Ответ нужно обосновать.

Ответ: 12

16)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.

Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.

17)Замените буквы A, B, C, D, E, F, G, K цифрами от 1 до 8 без повторений так, чтобы числа 6, 11, 16, 21 в серых треугольниках являлись суммами цифр, стоящих в трёх белых треугольниках, соседствующих по сторонам с серым.

Ответ: подходящие значения букв: А=2, В=3, С=5, D=1, Е=8, F=4, G=6, К=7. Легко проверить, что условие задачи выполняется.

18)Рыбак поймал 6 кг рыбы. Часть приготовил себе, остальное отдал трём котам. Каждый кот съедает в 2 раза больше рыбы, чем рыбак за одно и то же время. Сколько килограммов рыбы было отдано котам, если есть все начали одновременно, а коты съели свою часть в 2 раза быстрее, чем рыбак?

Ответ: 4,5 кг.

19)Три одинаковых кубика приставлены друг к другу гранями с одинаковым числом очков. Найдите сумму чисел на трёх нижних гранях кубиков данной конструкции, на верхних гранях которых числа 3, 5 и 6.

Ответ: 7

20)Лиса Алиса, Буратино и Пьеро нашли 110 золотых монет. Алиса предложила разложить их на три кучки и сказала: «Пусть жребий определит, кому какая достанется!» Чтобы мальчики не расстраивались, они договорились уравнять свои кучки по меньшей, а лишнее отдать Алисе. (Например, если Буратино достанется 10 монет, Пьеро – 15, а Алисе – 85 монет, то Пьеро отдаст Алисе 5 монет, чтобы у него с Буратино стало поровну). Алисе необходимо разложить все монеты на три кучки так, чтобы в результате ей наверняка досталось не меньше 100 золотых монет. Сколько у нее есть вариантов?

Ответ: 15

21)Сколько раз в последовательности из 12 чисел: 2, _, _, _, _, _, _, _, _, _, _,1 (на первом месте стоит 2, на последнем месте 1) встретится цифра 2, если известно, что сумма любых трех чисел, идущих подряд, равна 5?

Ответ: 8 раз

22)На турнир «рыцарей и лжецов» математического кружка ребята мастерили из квадратного листа картона размером 150см×150см стену рыцарского замка. По краям и в середине было вырезано три одинаковых квадрата. Петя заметил, что при этом периметр первоначального листа увеличился на 8%. Найдите площадь получившейся «стены».

Ответ: 20772 см2

23)Петя и Вася живут в одном доме и выходят в школу одновременно. Петя сначала считает ворон и идет со скоростью 4 км/ч, но ровно на середине пути на парковке пересаживается на велосипед и едет со скоростью 12 км/ч. Вася идет в школу с постоянной скоростью и приходит в школу одновременно с Петей. Учитель Степан Иванович на середине пути обгоняет Петю на мопеде, так как его скорость в 5 раз больше скорости Васи, он приезжает в щколу на 3 минуты раньше мальчиков. Найдите расстояние от дома мальчиков до школы.

Ответ: 2км

24)По данным, изображенным на рисунке справа, найти длину катета BC прямоугольного треугольника АВС.

Ответ: 12

25)Какое наибольшее число «тетраминошек» (как на рисунке) можно разместить внутри квадрата 6×6 без наложений? Фигурки можно как угодно поворачивать и переворачивать.

Ответ: 8

26)Назовем прямоугольник «симпатичным», если его длинная сторона меньше удвоенной короткой. (В частности, квадрат является симпатичным прямоугольником). Разрежьте квадрат площади 100 на четыре симпатичных прямоугольника с площадями 10, 20, 30 и 40.

28)Винни-Пух заготовил мёд на зиму в нескольких полных горшочках по 5 литров каждый. Если бы он свои запасы мёда разлил в 4-литровые горшочки, то их потребовалось бы на четыре больше, правда, один горшочек оказался бы неполным. А если разлить весь мёд в горшочки по 7 литров, то их потребовалось бы на четыре меньше первоначального количества. Но один горшочек снова оказался бы неполным. Сколько горшочков мёда заготовил Винни-Пух?

29)Из вершин А, В и С треугольника АВС провели соответственно медиану АМ, биссектрису ВK и высоту СH. Оказалось, что середина отрезка ВK совпадает с серединой отрезка MH. Найдите углы треугольника АВС.

30)На каникулах для всех желающих провели турнир по шашкам. Каждый сыграл с каждым ровно одну партию. За победу в партии участник турнира получал 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Известно, что среди участников мальчиков было в десять раз больше, чем девочек, и они вместе набрали в 4,5 раза больше очков, чем девочки. Сколько очков набрала самая успешная девочка?

31)Девятиклассник Дима выписывает ряд последовательных трёхзначных чисел так, чтобы каждое число делилось нацело на свою последнюю цифру. Какое наибольшее количество чисел могло быть в этом ряду?

32)Имеется сталь двух сортов с содержанием никеля 55% и 12%. Сколько нужно взять металла каждого из сортов, чтобы получить 2021 т стали с содержанием 32% никеля?

33)Вася выписывает последовательность из 2021 натуральных чисел, начиная с некоторого числа, так, чтобы сумма любых трех подряд идущих чисел была равна 5. Какое наибольшее количество двоек у него может получиться?

34)На стороне ВС треугольника АВС выбрана точка F. Оказалось, что отрезок AF пересекает медиану BD в точке Е так, что АЕ = ВС. Докажите, что BF = FE.

35)Имеются две бочки с водой бесконечной вместимости и два ковшика объемами 2 и 2 2 литров. Можно ли, пользуясь этими ковшиками, перелить из одной бочки в другую ровно 1 литр?

36)От 2 кусков сплавов с разным содержанием свинца массой 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого сплава, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы отрезанных кусков?

37)Художник Петров красит плоскость в два цвета произвольным образом, а геометр Васильев утверждает, что сможет построить треугольник с вершинами одного цвета, величины углов которого относятся как 4:2:1. Прав ли он?

Источник

В отряде 27 туристов какое наименьшее количество лодок надо взять на лодочной станции чтобы всем

Задача 1: (5–7) В поход пошли 20 туристов. Самому старшему из них 35 лет, а самому младшему 20 лет. Верно ли, что среди туристов есть одногодки?

Задача 2: (5–9) На столе стоят 16 стаканов. Из них 15 стаканов стоят правильно, а один перевернут донышком вверх. Разрешается одновременно переворачивать любые четыре стакана. Можно ли, повторяя эту операцию, поставить все стаканы правильно?

Решение: Посмотрим, как изменяется количество правильно стоящих стаканов при каждой такой операции. Очевидно, что это зависит от того, сколько из переворачиваемых стаканов стоят правильно, а сколько — вверх дном. А именно: — если все четыре переворачиваемых стакана стоят правильно, то количество правильно стоящих стаканов уменьшится на 4; — если из четырех стаканов правильно стоят три, то это количество уменьшится на 2; — если два, то количество не изменится; — если один, то увеличится на 2; — если все переворачиваемые стаканы стояли вверх дном, то количество правильно стоящих стаканов увеличится на 4.

В любом случае количество правильно стоящих стаканов либо остается прежним, либо изменяется на четное число. Поскольку сначала таких стаканов 15, то и в любой момент их будет нечетное количество. Поэтому добиться того, чтобы 16 стаканов стояли правильно, нельзя.

Задача 3: (5–7) Придя в тир, Петя купил 5 пуль. За каждый успешный выстрел ему дают еще 5 пуль. Петя утверждает, что он сделал 50 выстрелов и 8 раз попал в цель, а его друг Вася говорит, что этого не может быть. Кто из мальчиков прав?

Решение: Если Петя купил вначале 5 пуль, а всего сделал 50 выстрелов, то 45 пуль он получил за успешные выстрелы. Но для этого ему надо было попасть в цель 9 раз. А он утверждает, что сделал только 8 метких выстрелов. Значит, он не прав.

Задача 4: (5–7) Какое наименьшее число карточек спортлото (6 из 49) надо купить, чтобы наверняка хоть в одной из них был угадан хоть один номер?

Решение: Покажем, что восьми карточек достаточно. Заполним их следующим образом: в первой зачеркнем числа от 1 до 6, во второй — от 7 до 12 и т. д., в последней — от 43 до 48. Не зачеркнутым ни в одной карточке останется только число 49. Поэтому среди выигрышных номеров по крайней мере пять окажутся зачеркнутыми (к сожалению, нельзя гарантировать, что эти пять номеров будут зачеркнуты в одной карточке).

Теперь нам нужно доказать, что семи карточек может не хватить. Действительно, всего будет вычеркнуто не более 42 различных чисел. Поэтому не менее семи чисел окажутся не вычеркнутыми ни в одной из карточек. Может так случиться, что выигрышными окажутся как раз шесть чисел из этих семи.

Задача 5: (5–7) Два гроссмейстера по очереди ставят на шахматную доску ладьи (за один ход — одну ладью) так, чтобы они не били друг друга. Тот, кто не сможет поставить ладью, проигрывает. Кто выигрывает при правильной игре — первый или второй гроссмейстер?

Задача 6: (5) Дано 25 чисел. Сумма любых четырех из них положительна. Докажите, что сумма их всех тоже положительна.

Решение: Среди данных чисел должно быть хотя бы одно положительное. Действительно, возьмем любые четыре из этих чисел. Если бы все они были неположительны, то и их сумма была бы неположительной, что противоречит условию. (На самом деле, таким образом доказывается более сильное утверждение — что положительных чисел в данном наборе не меньше 22, однако нам понадобится существование лишь одного такого числа.) Выберем это положительное число. Остальные 24 числа разобьем произвольным образом на шесть четверок. Сумма всех 25 чисел — это сумма выбранного числа (которое положительно по выбору) и сумм получившихся четверок (которые положительны по условию). Она является положительной.

Задача 7: (6–9) Петя и Вася выписывают 12-значное число, ставя цифры по очереди, начиная со старшего разряда. Начинает Вася. Докажите, что какие бы цифры он не писал, Петя всегда сможет добиться, чтобы получившееся число делилось на 9.

Решение: Число делится на 9, если сумма его цифр делится на 9 (См. Т8). Поэтому одна из возможных стратегий для Пети — дополнять на каждом ходу Васину цифру до 9. То есть, если Вася пишет «0″, то Петя пишет «9″, если Вася пишет «1″, то Петя пишет «8″ и т.д. Таким образом, после каждой пары ходов Васи и Пети сумма цифр будет увеличиваться на 9. К моменту написания всего числа она станет равной .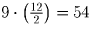

Заметим, что указанная стратегия не единственна. Попробуйте доказать, что независимо от того, какие цифры будут стоять перед последним ходом Пети в одиннадцати разрядах, своим последним ходом Петя сможет добиться, чтобы число делилось на 9. То есть все цифры кроме последней Петя может ставить произвольно!

Задача 8: (6–7) Четыре дома расположены по окружности. Где надо вырыть колодец, чтобы сумма расстояний от домов до колодца была наименьшей?

Решение: Обозначим дома буквами A, B, C, D в порядке их следования по окружности. Предположим, колодец вырыт в точке O. Из неравенства треугольника (см. Т17) следует, что OA + OC ≥ AC, причем равенство достигается тогда и только тогда, когда точка O принадлежит отрезку AC. Аналогично, OB + OD ≥ BD, причем равенство имеет место тогда и только тогда, когда O лежит на отрезке BD. Складывая эти неравенства, получим: OA + OB + OC + OD ≥ AC + BD. Равенство выполняется только тогда, когда O — точка пересечения отрезков AC и BD.

Поэтому колодец нужно вырыть в точке пересечения диагоналей четырехугольника ABCD.

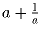
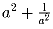
Задача 9: (6–7) Известно, что число — целое. Докажите, что число — тоже целое.

Решение: Доказательство следует из формулы:

Задача 10: (8–9) В турнире по олимпийской системе (проигравший выбывает) участвует 50 боксеров. Какое наименьшее количество боев надо провести, чтобы выявить победителя?

Решение: После каждого боя из соревнований выбывает один боксер — проигравший в этом бою. Поскольку всего к концу соревнований выбыть должны все, кроме победителя, всего должно быть 49 боев, независимо от того, как составляется расписание.

Задача 11: (8–9) Вершины одного параллелограмма лежат на сторонах другого — по одной вершине на каждой стороне. Докажите, что центры этих параллелограммов совпадают.

Решение: Пусть A, B, C, D — вершины одного параллелограмма, лежащие на сторонах a, b, c, d другого параллелограмма соответственно (рис. 14). Пусть O — центр параллелограмма ABCD. При симметрии относительно точки O точки A и C, а также точки B и D попарно переходят друг в друга. Прямая a переходит в параллельную ей прямую, проходящую через точку C — образ точки A, то есть в прямую c. Аналогично, прямая b переходит в прямую d. Значит, «внешний» параллелограмм при этой симметрии переходит в себя, то есть точка O является его центром.

Задача 12: (8–9) Было 7 ящиков. В некоторые из них положили еще по 7 ящиков и т. д. В итоге стало 10 непустых ящиков. Сколько всего стало ящиков?

Решение: При каждой операции заполняется один пустой ящик. Поскольку стало 10 непустых ящиков, то было проведено 10 операций. Вначале было 7 ящиков, и при каждой операции добавлялось еще по 7. Поэтому в результате стало 77 ящиков.

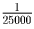
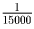
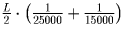
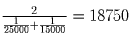
Решение: Каждый километр пробега передних покрышек изнашивает их на ,, а задних — на ,. Поэтому если в середине пути длиной L,км покрышки поменять, то их износ за весь путь будет равен . Приравняв эту величину единице, мы получим путь, который можно пройти до полного износа покрышек. Он равен ,(км).

Очевидно, что сменить покрышки в середине пути — оптимальная стратегия, так как если это сделать в другом месте, то покрышки, прошедшие сзади больше, чем впереди, выйдут из строя раньше. Значит, поменять покрышки надо через 9375,км пути.

Задача 14: (8–9) Найдите наибольшее отношение трехзначного числа к сумме его цифр.

Решение:

Рассмотрим произвольное трехзначное число 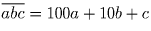и его отношение к своей сумме цифр. Имеем

В первом из двух неравенств равенство выполняется при c = 0, а во втором — при b = 0. Поэтому искомое наибольшее равно 100 и достигается для трехзначных чисел, записи которых оканчиваются двумя нулями.

Задача 15: (8–9) В классе каждый мальчик дружит ровно с двумя девочками, а каждая девочка — ровно с тремя мальчиками. Еще известно, что в классе 31 пионер и 19 парт. Сколько человек в этом классе?

Решение:

Обозначим количество мальчиков в классе через M, а девочек — через D. Из условий следует, что 31 ≤ D + M ≤ 38 и 3D = 2M. Последнее равенство показывает, что количество девочек четно, а количество мальчиков делится на 3. Более того, 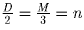, откуда D + M = 5n. Существует единственное целое число, заключенное между 31 и 38, делящееся на 5. Поэтому можно утверждать, что в классе 35 учеников — 14 девочек и 21 мальчик.

Задача 16: (8–9) Каждый из четырех гномов — Беня, Веня, Женя, Сеня — либо всегда говорит правду, либо всегда врет. Мы услышали такой разговор: Беня — Вене: «ты врун»; Женя — Бене: «сам ты врун»; Сеня — Жене: «да оба они вруны, — (подумав), — впрочем, ты тоже». Кто из них говорит правду?

Решение:

Предположим, Сеня говорит правду. Тогда, согласно его словам, три остальных гнома — вруны. И, тем самым, фраза Бени является правдой. Значит, предположение приводит к противоречию, поэтому Сеня — врун, и его утверждение, что Женя — врун, является ложным. Отсюда заключаем, что Женя говорит правду. Тем самым, Беня — врун, а Веня говорит правду. Отметим, что фраза Сени «да оба они вруны» (относительно Бени и Вени) является ложной (несмотря на то, что Беня действительно врун), поскольку Веня — не врун.

Задача 17: (8–9) В классе 25 человек. Известно, что среди любых трех из них есть двое друзей. Докажите, что есть ученик, у которого не менее 12 друзей.

Решение:

Рассмотрим двоих учеников класса, которые не дружат между собой. (Если таких нет, то все ученики класса дружат между собой, значит, у каждого ученика имеется 24 друга, и задача решена.) Пусть этими двумя будут Вася и Петя. Тогда из оставшихся 23 учеников каждый дружит либо с Васей, либо с Петей. Действительно, если бы кто-то (скажем, Коля) не дружил бы ни с Васей, ни с Петей, то мы имели бы троих учеников, среди которых не было бы друзей. Теперь если предположить, что и Вася, и Петя имеют не более 11 друзей, то всего в классе, кроме этих двоих было бы не больше 22 человек (см. Т2). Полученное противоречие показывает, что один из школьников имеет не менее 12 друзей.

Задача 18: (8–9) Между соседними лагерями 1 день пути. Экспедиции требуется перенести 1 банку консервов в лагерь, находящийся в 5 днях пути от базового и вернуться обратно. При этом: — каждый член экспедиции может нести с собой не более 3 банок консервов; — за 1 день он съедает 1 банку консервов; — оставлять консервы можно только в лагерях. Какое наименьшее количество банок консервов придется взять из базового лагеря для этой цели?

Решение:

Предположим, что в каждом лагере имеется торговая палатка, где продаются доставленные консервы. Пусть цена одной банки в базовом лагере равна одному рублю, а в каждом следующем — в три раза больше, чем в предыдущем. В таком случае цена банок, доставленных в любой из лагерей не меньше, чем цена банок, взятых для этого из базового лагеря. Действительно, для переноски банки из некоторого лагеря в следующий мы должны взять по крайней мере три банки, две из которых будут съедены на пути туда и обратно соответственно. Стоимость банки в пятом лагере будет при этом 3 5 = 243,руб., значит из базового лагеря нужно взять не менее 243 банок.

Докажем теперь, что 243 банок хватит. Для этого из базового лагеря выходит 81 член экспедиции. 54 человека из них, принеся по банке в первый лагерь, сразу возвращаются. Остальные 27 человек, взяв по три банки, идут во второй лагерь. 27 банок при этом остаются в первом лагере, чтобы обеспечить им возвращение из первого лагеря в базовый. Так происходит в каждом лагере. Две трети дошедших участников возвращаются, а треть — идет дальше. Таким образом, из четвертого лагеря в пятый выйдет один человек. Он и принесет вожделенную банку в пятый лагерь.

Источник