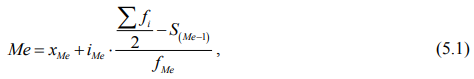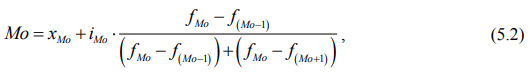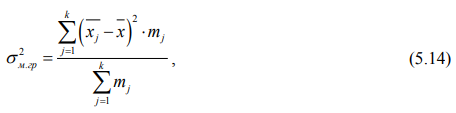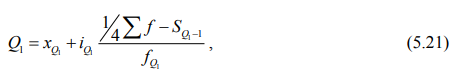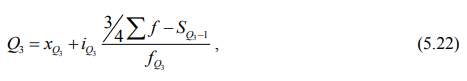вариационный ряд это ряд распределения построенный по какому признаку
Сводка и группировка статистических данных
3.3. Ряды распределения: виды, правила построения, графическое изображение
Ряды распределения делятся на атрибутивные и вариационные, в зависимости от признака, положенного в основу группировки. Если признак качественный, то ряд распределения называется атрибутивным. Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности (см. табл. 3.1).
Если признак, по которому строится ряд распределения, количественный, то ряд называется вариационным.
Вариационные ряды бывают дискретными и интервальными. У дискретных рядов (табл. 3.7) варианты выражены конкретными числами, чаще всего целыми.
| Время работы в компании, полных лет (варианты) | Число работающих | |
|---|---|---|
| Человек (частоты) | в % к итогу (частости) | |
| до года | 15 | 11,6 |
| 1 | 17 | 13,2 |
| 2 | 19 | 14,7 |
| 3 | 26 | 20,2 |
| 4 | 10 | 7,8 |
| 5 | 18 | 13,9 |
| 6 | 24 | 18,6 |
| Итого | 129 | 100,0 |
Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда. При непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения.
3.3.1. Построение дискретных вариационных рядов
Рассмотрим методику построения дискретных вариационных рядов на примере.
Пример 3.2. Имеются следующие данные о количественном составе 60 семей:
| 2 3 3 1 4 2 3 3 1 5 2 4 3 2 2 1 2 3 4 5 |
| 2 2 1 3 4 3 3 3 6 6 3 3 6 1 3 4 3 4 4 5 |
| 3 3 2 2 1 3 2 5 5 2 4 3 6 1 2 2 3 1 3 4 |
Для того чтобы получить представление о распределении семей по числу их членов, следует построить вариационный ряд. Поскольку признак принимает ограниченное число целых значений строим дискретный вариационный ряд. Для этого сначала рекомендуется выписать все значения признака (число членов в семье) в порядке возрастания (т.е. провести ранжирование статистических данных):
| 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 |
| 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
| 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 |
| Число членов семьи (х) | Число семей (y) |
|---|---|
| 1 | 8 |
| 2 | 14 |
| 3 | 20 |
| 4 | 9 |
| 5 | 5 |
| 6 | 4 |
| Итого | 60 |
3.3.2. Построение интервальных вариационных рядов
Покажем методику построения интервальных вариационных рядов распределения на следующем примере.
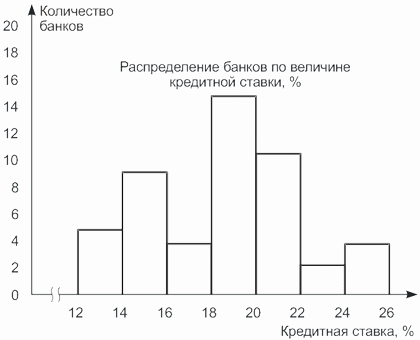
Пример 3.3. В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):
| 14,7 | 19,0 | 24,5 | 20,8 | 12,3 | 24,6 | 17,0 | 14,2 | 19,7 | 18,8 |
| 18,1 | 20,5 | 21,0 | 20,7 | 20,4 | 14,7 | 25,1 | 22,7 | 19,0 | 19,6 |
| 19,0 | 18,9 | 17,4 | 20,0 | 13,8 | 25,6 | 13,0 | 19,0 | 18,7 | 21,1 |
| 13,3 | 20,7 | 15,2 | 19,9 | 21,9 | 16,0 | 16,9 | 15,3 | 21,4 | 20,4 |
| 12,8 | 20,8 | 14,3 | 18,0 | 15,1 | 23,8 | 18,5 | 14,4 | 14,4 | 21,0 |
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения.
Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса
Для нашего примера получим: n = 1 + 3,322lgN = 1 + 3,322lg50 = 6,6 » 7.
Для нашего примера
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0.
Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0-14,0; 14,0-16,0; 16,0-18,0; 18,0-20,0; 20,0-22,0; 22,0-24,0; 24,0-26,0.
Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18-25, 26-33, 34-41, 42-49, 50-57, 58-65, 66 и более.
Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.д. записать: до 14,0; 24,0 и выше.
| Ставка банка % (варианты) | |||
|---|---|---|---|
| 12,3 | 17,0 | 19,9 | 23,8 |
| 12,8 | 17,4 | 20,0 | 24,5 |
| 13,0 | 18,0 | 20,0 | 24,6 |
| 13,3 | 18,1 | 20,4 | 25,1 |
| 13,8 | 18,5 | 20,4 | 25,6 |
| 14,2 | 18,7 | 20,5 | |
| 14,3 | 18,8 | 20,7 | |
| 14,4 | 18,9 | 20,7 | |
| 14,7 | 19,0 | 20,8 | |
| 14,7 | 19,0 | 21,0 | |
| 15,1 | 19,0 | 21,0 | |
| 15,2 | 19,0 | 21,1 | |
| 15,3 | 19,0 | 21,4 | |
| 16,0 | 19,6 | 21,9 | |
| 16,9 | 19,7 | 22,7 | |
При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу.
Результаты группировки, полученные в нашем примере, оформим в таблице.
| Краткая ставка, % | Количество банков, ед. (частоты) | Накопленные частоты |
|---|---|---|
| 12,0-14,0 | 5 | 5 |
| 14,0-16,0 | 9 | 14 |
| 16,0-18,0 | 4 | 18 |
| 18,0-20,0 | 15 | 33 |
| 20,0-22,0 | 11 | 44 |
| 22,0-24,0 | 2 | 46 |
| 24,0-26,0 | 4 | 50 |
| Итого | 50 | — |
В процессе группировки данных при построении вариационных рядов иногда используются неравные интервалы. Это относится к тем случаям, когда значения признака подчиняются правилу арифметической или геометрической прогрессии или когда применение формулы Стерджесса приводит к появлению «пустых» интервальных групп, не содержащих ни одной единицы наблюдения. Тогда границы интервалов задаются произвольно самим исследователем исходя из здравого смысла и целей обследования либо по формулам. Так, для данных, изменяющихся в арифметической прогрессии, величина интервалов вычисляется следующим образом:
Порядок расчетов границ неравных интервалов для данных, изменяющихся приблизительно в арифметической прогрессии, показан в табл. 3.15.
Для показателей, приблизительно изменяющихся в геометрической прогрессии, величину интервалов можно вычислить по формуле
Для графического изображения интервального ряда используют гистограмму, имеющую вид многоступенчатой фигуры, состоящей из прямоугольников. По оси абсцисс откладывают значения границ интервалов. Сами интервалы будут являться основаниями прямоугольников. Высота прямоугольников соответствует частоте или частости интервалов, которые откладываются по оси ординат.
По данным таблицы, приведенной в примере 3.3, построим гистограмму (рис. 3.2).
При неравных интервалах у гистограммы распределения высотами прямоугольников будут являться показатели плотности распределения, рассчитываемые как частное от деления частоты интервала на его величину.
Зависимость между значениями признака и накопленными частотами показывают особые графики, называемые кумулятой и огивой распределения.
В случае интервального ряда при построении кумуляты по оси абсцисс отмечают границы интервальных групп, накопленные частоты по оси ординат относят к верхним границам интервалов.
По данным таблицы, приведенной в примере 3.3, построим кумуляту распределения для интервального ряда (рис. 3.2).
Если у кумулятивной кривой поменять местами ось абсцисс с осью ординат, получим график, называемый огивой распределения (рис. 3.4).
Ряды распределения
Понятие о рядах распределения
Среди простых группировок особо выделяют ряды распределения.
Рядом распределения в статистике называется упорядоченное распределение единиц совокупности на группы по какому-либо признаку.
В зависимости от признака положенного в основание ряда распределения различают атрибутивные и вариационные ряды распределения.
Ряды распределения, построенные по описательному признаку, называются атрибутивными рядами.
Пример атрибутивного ряда распределения приведен по данным таблицы 3.5 в таблице 5.1.
| Группы предприятий по организационноправовой форме хозяйствования | Количество предприятий, ед. | Удельный вес предприятий, % |
|---|---|---|
| Государственные предприятия | 6 | 20 |
| Общества с ограниченной ответственностью | 17 | 56,7 |
| Фермерские хозяйства | 7 | 23,3 |
| Всего | 30 | 100,0 |
Ряды распределения, построенные по количественному признаку, называются вариационными рядами.
В вариационном ряду различают два элемента: варианты и частоты.
Вариантами (х) называются отдельные значения группировочного признака, которые он принимает в вариационном ряду, т.е. конкретные числовые значения признака единиц совокупности.
Числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения, называются частотами (f). Частоты могут быть даны и как относительные величины структуры (в процентах, или долях единицы, или в промилле). В этом случае их называют частостями.
Сумма всех частот определяет численность всей совокупности, т.е. ее объем (N).
По своей конструкции вариационный ряд состоит из двух столбцов: один столбец – значения варьирующего признака, другой – частоты или частости. Макет вариационного ряда приведен в таблице 5.2.
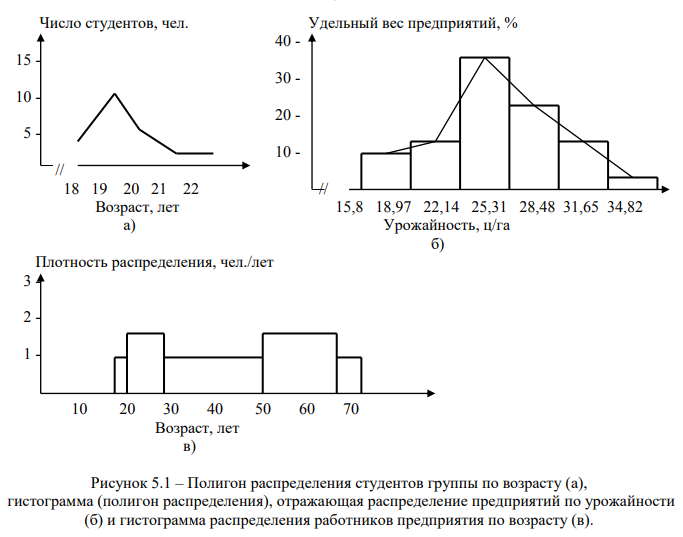
Для удобства вариационный ряд распределения может быть развернут (см. табл. 4.8). В таблице 4.2 возраст студентов представлен соответствующими вариантами, а число студентов – частотами.
Вариационные ряды по способу построения бывают двух видов: дискретные и интервальные.
Дискретные вариационные ряды характеризуются тем, что варианты в них имеют значения отдельных целых чисел. Пример дискретного вариационного ряда приведен в таблице 4.8.
Если число вариант велико или признак имеет непрерывную вариацию, то объединение значений отдельных наблюдений в группы возможно лишь посредством интервала.
Интервальные вариационные ряды характеризуются тем, что значения вариант в них заданы в виде интервалов.
Пример интервального вариационного ряда распределения приведен по данным таблицы 3.8 в таблице 5.3.
| Группы предприятий по по урожайности (х), ц/га | Количество предприятий (f), ед. | Удельный вес предприятий (f), % |
|---|---|---|
| 15,8-18,97 | 3 | 10 |
| 18,97-22,14 | 4 | 13,3 |
| 22,14-25,31 | 11 | 36,7 |
| 25,31-28,48 | 7 | 23,4 |
| 28,48-31,65 | 4 | 13,3 |
| 31,65-34,82 | 1 | 3,3 |
| Всего | 30 | 100,0 |
Приведенный в таблице 5.3 вариационный ряд показывает, что наиболее многочисленную группу составляют предприятия с урожайностью от 22,14 ц/га до 25,31 ц/га – 11 предприятий или 36,7 % от всей совокупности. В группах выше и ниже этой группы число предприятий убывает, причем в группах с более высокой урожайностью число предприятий больше. Так, количество предприятий в группах с урожайностью свыше 25,31 ц/га составляет 12 (7 + 4 + 1) или 40 % (23,4 + 13,3 + 3,3), а в группах ниже 22,14 ц/га – 7 (3 + 4) предприятий или 23,3 % (10 + 13,3).
Если вариационный ряд имеет группы с неравными интервалами, то частоты в отдельных интервалах непосредственно не сопоставимы, так как зависят от ширины интервала. Для того чтобы частоты можно было бы сравнить исчисляют плотность распределения – частоту (т.е. число единиц совокупности), рассчитанную на единицу ширины интервала.
Пример расчета плотности распределения приведен в таблице 5.4.
| Возраст работников, лет | Число работников, чел. | Плотность распределения, чел./год |
|---|---|---|
| 16-18 | 2 | 1,0 (2 : (18-16) = 2 : 2) |
| 18-25 | 12 | 1,7 |
| 25-45 | 20 | 1 |
| 45-60 | 26 | 1,7 |
| 60-65 | 5 | 1 |
| Всего | 65 | — |
Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат.
При дискретной вариации признака графиком вариационного ряда служит полигон распределения. Графическим изображением интервальных вариационных рядов служит гистограмма.
При неравных интервалах гистограмма строится только по плотности распределения. При построении графиков рядов распределения по оси абсцисс приводятся варианты, а по оси ординат – соответствующие им частоты (частости).
Примеры полигона распределения и гистограммы, построенные по данным таблиц 4.8, 5.3 и 5.4, приведены на рис. 5.1.
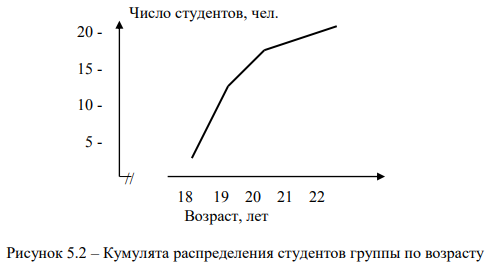
Для иллюстрации рядов распределения используются также кумуляты и огивы. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумулята) или частостей (огива), соответствующих этим значениям признака.
Кумулята распределения студентов по возрасту приведена на рис. 5.2.
Вариационные ряды дают возможность установить характер распределения единиц совокупности по тому или иному количественному признаку с помощью расчета четырех видов характеристик (групп показателей), указанных на рис. 5.3.
Анализ показателей, характеризующих центральную тенденцию ряда распределения, степень вариации, дифференциации и концентрации значений варьирующего признака, а также форму их распределения, позволяет дать комплексную оценку характера распределения единиц совокупности (комплексную характеристику строения исследуемого социально-экономического явления).
Мода и медиана
Для характеристики центральной тенденции (положения центра) ряда распределения кроме средней арифметической величины применяются структурные средние: медиана и мода, используемые для изучения внутреннего строения рядов распределения значений признаков.
В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризуют значение признака у единицы совокупности, занимающей определенное положение в вариационном ряду распределения.
Медиана – значение признака единицы совокупности, стоящей в середине упорядоченного ряда и делящей совокупность на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
Медиану используют как наиболее надежный показатель типичного значения признака единиц неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений.
В дискретном вариационном ряду медианой следует считать значение признака в той группе единиц совокупности, в которой накопленная частота превышает половину численности совокупности. Например, по данным таблицы 4.8 медиана равна 19 лет (2 + 11 > 20 : 2).
При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при десяти значениях признака – среднюю из пятого и шестого значений в ранжированном ряду.
В интервальном вариационном ряду для нахождения медианы (Ме) применяется формула:
где хМе – нижняя граница интервала, в котором находится медиана (медианного интервала);
iМе – величина медианного интервала;
Σfi – сумма частот ряда;
S(Ме – 1) – накопленная частота в интервале, предшествующем медианному;
fМе – частота медианного интервала.
При нечетном числе единиц совокупности номер медианы равен не Σfi /2, а (Σfi + 1)/2.
Пример расчета медианы
По данным таблицы 4.13 следует найти медианное значение заработной платы работников предприятия. Для этого предварительно рассчитаем значения накопленных частот для каждого интервала, приведенные в таблице 5.5.
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Накопленная частота, чел. (SМе) |
|---|---|---|
| 8000-10000 | 20 | 20 |
| 10000-12000 | 80 | 100 (20 + 80) |
| 12000-14000 | 160 | 260 (100 + 160) |
| 14000-16000 | 90 | 350 (260 + 90) |
| 16000-18000 | 40 | 390 (350 + 40) |
| 18000 и выше | 10 | 400 (390 + 10) |
| Всего | 400 | – |
Медианным является срединное из 400 значений ряда распределения, т. е. 200-е от начала ряда распределения значение заработной платы (400 : 2), которое находится в третьем интервале, что видно из ряда накопленных частот (260 >200). Третий интервал является медианным.
По формуле 5.1: Ме = 13250 руб., т. е. одна половина работников предприятия имеет заработную плату меньше 13250 руб., а другая – больше.
Модой называется варианта (значение признака), которая в изучаемом ряду распределения встречается чаще всего.
Например, в дискретном вариационном ряду это варианта, имеющая наибольшую частоту.
По данным таблицы 4.8 мода также равна 19 лет, так как это наиболее часто встречающийся возраст студентов в их группе (11 человек).
Если два или несколько значений признака встречаются равное количество раз, вариационный ряд считается бимодальным или мультимодальным. Это говорит о неоднородности совокупности.
В интервальном вариационном ряду модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т. е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение считается точечной модой.
В интервальном вариационном ряду для нахождения моды (Мо) применяется формула:
где хМо – нижняя граница модального интервала (наиболее часто встречающегося);
iМо – величина модального интервала;
fМо – частота модального интервала;
f(Мо – 1) – частота интервала, предшествующего модальному;
f(Мо + 1) – частота интервала, следующего за модальным.
Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и др.
Пример расчета моды
По данным таблицы 4.13 нужно найти модальное значение заработной платы работников предприятия.
Модальным является третий интервал, имеющий наибольшую частоту (160 чел.).
По формуле 5.2: Мо = 13066,67 руб., т.е. наибольшее число работников предприятия имеет заработную плату 13066,67 руб.
При выборе конкретного показателя центра распределения исходят из таких рекомендаций:
– для устойчивых социально-экономических процессов (однородных совокупностей) в качестве показателя центра используют среднюю арифметическую величину. Такие процессы характеризуются симметричными распределениями, в которых х = Ме = Мо;
– для неустойчивых процессов положение центра распределения характеризуется с помощью моды или медианы. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической величиной и модой: х х > Ме > Мо.
Показатели вариации
При определении общего характера распределения важнейшей задачей является оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной вариации значений признака.
Вариация, т.е. несовпадение уровней значений признаков у единиц совокупности, имеет объективный характер, так как численный уровень значений признака определяется конкретными условиями, в которых находится каждая из изучаемых единиц совокупности, а также особенностями их развития. Вариация помогает познать сущность изучаемого явления.
Для измерения вариации в статистике применяют несколько способов.
Наиболее простым является расчет показателя «размах вариации» (R), представляющего собой разницу между максимальным и минимальным значением наблюдаемого признака, по формуле:
где хmax и хmin – соответственно, максимальное и минимальное значение признака в исследуемой срвокупности.
Размах вариации охватывает только крайние отклонения значений признака, но не отражает отклонений от средней величины всех вариант в ряду. Чем больше размах вариации, тем менее однородна исследуемая совокупность.
Точнее характеризуют вариацию признака показатели, основанные на учете колеблемости (отклонений) всех значений признака от его среднего уровня. От величины этих отклонений зависит типичность и надежность средних характеристик исследуемой совокупности.
Средние отклонения значений признаков каждой единицы совокупности от среднего значения признака в целом отражают показатели вариации. Показатели вариации используют для оценки степени однородности исследуемой совокупности по варьирующему признаку и типичности средней величины.
Простейший показатель такого типа – среднее линейное отклонение, представляющее собой среднее арифметическое значение абсолютных отклонений признака от его среднего уровня.
Среднее линейное отклонение ( d ) по несгруппированным данным рассчитывается по формуле:
Среднее линейное отклонение ( d ) по сгруппированным данным рассчитывается по формуле:
Чем меньше среднее линейное отклонение, тем более однородны значения признака изучаемого явления.
Основной недостаток показателя среднего линейного отклонения заключается в том, что при его расчетах пренебрегают знаками, следовательно, конечный результат получается со значительной погрешностью. Для того чтобы расчет был более точным, определяют средний квадрат отклонений (дисперсию), представляющий собой средний квадрат отклонений значений признака от его среднего уровня.
Дисперсия (σ 2 ) по несгруппированным данным рассчитывается по формуле:
Дисперсия (σ 2 ) по сгруппированным данным рассчитывается по формуле:
Среднее квадратическое отклонение (σ) рассчитывается по формуле:
Среднее квадратическое отклонение является абсолютной мерой вариации и зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней, что не позволяет непосредственно сравнивать средние квадратические отклонения вариационных рядов с разными уровнями. Среднее квадратическое отклонение выражается в тех же единицах измерения, что и усредняемые значения признака исследуемой совокупности.
Для сравнительной характеристики вариационных рядов с разными уровнями по степени надежности их средней величины и однородности исследуемых совокупностей рассчитывается относительная мера вариации – коэффициент вариации.
Коэффициент вариации (V) в процентном выражении рассчитывается по формуле:
Чем больше значение коэффициента вариации, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна (типична) средняя величина.
Вместе с тем, конкретное значение коэффициента вариации не всегда позволяет однозначно характеризовать степень ее интенсивности и однородность исследуемой совокупности. Оценка степени интенсивности вариации должна учитывать особенности единиц наблюдения и признаков, их характеризующих. В частности, для совокупности сельхозяйственных предприятий вариация урожайности в одном и том же природном регионе может быть оценена как слабая, если V 25%. Напротив, вариация роста в совокупности взрослых мужчин или женщин уже при V = 7%, должна быть оценена и восприниматься как сильная.
Таким образом, оценка интенсивности вариации состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив. Если различия в урожайности, заработной плате или доходе на душу населения в несколько раз воспринимаются как вполне естественные, то различия в росте людей хотя бы в полтора раза уже воспринимаются как очень сильные.
Пример расчета показателей вариации
По данным таблицы 4.13 необходимо охарактеризовать ряд распределения работников предприятия по заработной плате на предмет его однородности и типичности среднего значения уровня заработной платы для работников предприятия.
По формуле 5.3 размах вариации (R = 20000 – 8000 = 12000 руб.), т.е. разница между максимальным и минимальным уровнем оплаты труда на предприятии составляет 12000 руб. На первый взгляд это достаточно большой разброс в оплате труда работников предприятия, т.е. исследуемая совокупность не однородна по уровню оплаты труда. Данное предположение подтвердится или нет последующими расчетами. Отметим, что верхнюю границу последнего открытого интервала определили исходя их величины смежного с ним интервала, которая равна 2000 руб. (18000 – 16000), 18000 + 2000 = 20000 руб.
Расчет среднего линейного отклонения проведем с помощью данных таблицы 5.6.
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | |xi— X | | |xi— X | × fi |
|---|---|---|---|---|
| 8000-10000 | 20 | 9000 | 4400 | 88000 |
| 10000-12000 | 80 | 11000 | 2400 | 192000 |
| 12000-14000 | 160 | 13000 | 400 | 64000 |
| 14000-16000 | 90 | 15000 | 1600 | 144000 |
| 16000-18000 | 40 | 17000 | 3600 | 144000 |
| 18000 и выше | 10 | 19000 | 5600 | 56000 |
| Всего | 400 | – | – | 688000 |
Средняя заработная плата работников предприятия, рассчитанная по формуле 4.22 ( X ), равна 13400 руб.
По формуле 5.5: d = 1720 руб.
Расчет дисперсии (среднего квадрата отклонений) и среднего квадратического отклонения проведем с помощью данных таблицы 5.7
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | (xi— X ) 2 | (xi— X ) 2 × fi |
|---|---|---|---|---|
| 8000-10000 | 20 | 9000 | 19360000 | 387200000 |
| 10000-12000 | 80 | 11000 | 5760000 | 460800000 |
| 12000-14000 | 160 | 13000 | 160000 | 25600000 |
| 14000-16000 | 90 | 15000 | 2560000 | 230400000 |
| 16000-18000 | 40 | 17000 | 12960000 | 518400000 |
| 18000 и выше | 10 | 19000 | 31360000 | 313600000 |
| Всего | 400 | – | – | 1936000000 |
По формуле 5.7: σ 2 = 4840000.
По формуле 5.8: σ = 2200 руб.
На основании полученных показателей вариации трудно с уверенностью оценить однородность работников предприятия по уровню их заработной платы.
По формуле 5.9: V = 16,4%, что говорит о достаточной однородности исследуемой совокупности по уровню зарплаты и типичности ее среднего уровня.
Дисперсия обладает рядом математических свойств, упрощающих технику ее расчета. В частности:
Эти свойства положены в основу расчета дисперсии способом моментов. Способ моментов применим в том случае, если задан интервальный ряд с равными интервалами.
Дисперсия методом моментов рассчитывается по формуле:
где h – шаг интервала; m’, m» – соответственно моменты первого и второго порядка. Момент первого порядка рассчитывается по формуле 4.32. Момент второго порядка рассчитывается по формуле:
Пример расчета дисперсии методом моментов
На основе данных таблицы 4.13 рассчитаем дисперсию методом моментов. Для этого построим вспомогательную таблицу 5.8, используя данные таблицы 4.15 и комментарии к ней.
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | (xi-A)/h | [(xi-A)/h] 2 | [(xi-A)/h] 2 × fi |
|---|---|---|---|---|---|
| 8000-10000 | 20 | 9000 | -2 | 4 | 80 |
| 10000-12000 | 80 | 11000 | -1 | 1 | 80 |
| 12000-14000 | 160 | 13000 | 0 | 0 | 0 |
| 14000-16000 | 90 | 15000 | 1 | 1 | 90 |
| 16000-18000 | 40 | 17000 | 2 | 4 | 160 |
| 18000 и выше | 10 | 19000 | 3 | 9 | 90 |
| Всего | 400 | – | – | – | 500 |
По формуле 4.32: m’ = 0,2.
По формуле 5.11: m» = 1,25.
По формуле 5.10: σ 2 = 4840000, что равно значению дисперсии, полученному по данным таблицы 5.7, по формуле 5.7.
Для расчета дисперсии в любых рядах распределения (дискретных и интервальных с равными и неравными интервалами) применяется другой упрощенный метод расчета дисперсии – способ разности.
Дисперсия способом разности рассчитывается по формуле:
где x – среднее значение варьирующего признака, исчисленное по формуле 4.22;
x 2 – среднее значение квадратов вариант, рассчитываемое по формуле:
Пример расчета дисперсии методом разности
Дисперсию методом разности рассчитаем по данным таблицы 4.13.
Средняя заработная плата работников предприятия, исчисленная ранее: x = 13400 руб.
Для расчета среднего значения квадратов вариант составим вспомогательную таблицу 5.9.
| Группы работников по уровню заработной платы, руб. | Число работников, чел. (fi) | Середина интервала, руб. (xi) | xi 2 | xi 2 × fi |
|---|---|---|---|---|
| 8000-10000 | 20 | 9000 | 81000000 | 1620000000 |
| 10000-12000 | 80 | 11000 | 121000000 | 9680000000 |
| 12000-14000 | 160 | 13000 | 169000000 | 27040000000 |
| 14000-16000 | 90 | 15000 | 225000000 | 20250000000 |
| 16000-18000 | 40 | 17000 | 289000000 | 11560000000 |
| 18000 и выше | 10 | 19000 | 361000000 | 3610000000 |
| Всего | 400 | – | – | 73760000000 |
По формуле 5.13: x 2 = 184400000.
По формуле 5.12: σ 2 = 184400000 – 13400 2 = 4840000, что совпадает со значения дисперсии, найденными другими способами.
Виды дисперсии. Понятие об эмпирическом коэффициенте детерминации и эмпирическом корреляционном отношении
Вариация признака определяется различными факторами, в результате чего различают общую дисперсию, межгрупповую дисперсию и внутригрупповую дисперсию.
Общая дисперсия (σ 2 ) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.
Межгрупповая дисперсия (σ 2 м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки, и рассчитывается по формуле:
где k – количество групп, на которые разбита вся совокупность;
mj – количество объектов, наблюдений, включенных в группу j;
x j – среднее значение признака по группе j;
x – общее среднее значение признака.
Внутригрупповая дисперсия (σ 2 j,вн.гр) отражает случайную вариацию, т.е. часть вариации, возникающую под влиянием неучтенных факторов и независящую от признака-фактора, положенного в основание группировки, и рассчитывается по формуле:
или, на основе метода разностей, по формуле:
где xij – значение i-ой варианты в группе j.
Если в сформированных группах отдельные данные встречаются не один раз, то для расчета внутригрупповой дисперсии используется формула средней арифметической взвешенной.
Среднее значение внутригрупповых дисперсий рассчитывается по формуле:
Существует закон, согласно которому общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака и дисперсии, появляющейся под влиянием всех прочих факторов.
Правило сложения дисперсий выражается формулой:
Правило сложения дисперсии широко применяется при исчислении тесноты связей между признаками (факторным и результативным). Для этого определяют эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.
Эмпирический коэффициент детерминации показывает, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки.
Эмпирический коэффициент детерминации (η 2 ) рассчитывается по формуле:
Эмпирическое корреляционное отношение показывает тесноту связи между признаками – группировочным и результативным.
Эмпирическое корреляционное отношение (η) рассчитывается по формуле:
Оно изменяется в пределах от 0 до 1. Характеристика связи между признаками при соответствующих значениях эмпирического корреляционного отношения приведена в таблице 5.10.
| Значение η | 0 | 0-0,2 | 0,2-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 | 1 |
|---|---|---|---|---|---|---|---|---|
| Характеристика связи | отсутствует | очень слабая | слабая | умеренная | заметная | тесная | очень тесная | функциональная |
Пример расчета общей, межгрупповой и внутригрупповой дисперсии, эмпирического коэффициента детерминации и эмпирического корреляционного отношения
Вариация урожайности зерновых культур сельскохозяйственных предприятий одного региона (см. табл. 3.3) обусловлена влиянием различных факторов: качеством земель, погодными условиями, уровнем агрокультуры и т.п. Уровень агрокультуры и состояние технической базы сельхозпроизводства определяется, в частности, организационно-правовой формой хозяйствования (предприятия).
По результатам комбинационной группировки сельскохозяйственных предприятий (см. табл. 3.10) можно предположить наличие зависимости урожайности от организационно-правовой формы предприятия. Необходимо оценить тесноту связи между урожайностью зерновых культур сельхозпредприятий и их организационно-правовой формой. В данном случае организационноправовая форма хозяйствования является группировочным фактором, урожайность зерновых культур – результативным.
По данным столбцов А, Б и 1 таблицы 3.10 построим таблицу 5.11, представляющую собой группировку сельскохозяйственных предприятий, имеющих разную урожайность зерновых культур, по их организационно-правовой форме.
Для расчета общей и внутригрупповых дисперсий составим таблицу 5.12.
В качестве хi примем середины интервалов урожайности зерновых культур, приведенных в табл. 5.11.
Средняя урожайность, рассчитанная по всей совокупности предприятий по формуле 4.22: 24,57 ц/га.
| Урожайность, ц/га (хi) | Количество предприятий, ед. (fi 0) | В том числе | ||
|---|---|---|---|---|
| государственных предприятий (fi 1) | обществ с ограниченной ответственностью (fi 2) | фермерских хозяйств (fi 3) | ||
| 15,8-18,97 | 3 | 2 | 1 | – |
| 18,97-22,14 | 4 | – | 4 | – |
| 22,14-25,31 | 11 | 3 | 8 | – |
| 25,31-28,48 | 7 | 1 | 3 | 3 |
| 28,48-31,65 | 4 | – | 1 | 3 |
| 31,65-34,82 | 1 | – | – | 1 |
| Всего | 30 | 6 | 17 | 7 |
| хi, ц/га | rowspan=2>fi 0 | хi × fi 0 | (хi— х0 ) 2 × fi 0 | Государственные предприятия | ||
|---|---|---|---|---|---|---|
| fi 1 | хi × fi 1 | (хi— х1 ) 2 × fi 1 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 17,385 | 3 | 52,155 | 154,87 | 2 | 34,770 | 45,22 |
| 20,555 | 4 | 82,220 | 64,48 | – | – | – |
| 23,725 | 11 | 260,975 | 7,85 | 3 | 71,175 | 7,54 |
| 26,895 | 7 | 188,265 | 37,84 | 1 | 26,895 | 22,61 |
| 30,065 | 4 | 120,260 | 120,78 | – | – | – |
| 33,235 | 1 | 33,235 | 75,08 | – | – | – |
| Всего | 30 | 737,110 | 460,90 | 6 | 132,840 | 75,37 |
Продолжение таблицы 5.12
| хi, ц/га | Общества с ограниченной ответственностью | Фермерские хозяйства | ||||
|---|---|---|---|---|---|---|
| fi 2 | хi × fi 2 | (хi— х2 ) 2 × fi 2 | fi 3 | хi × fi 3 | (хi— х3 ) 2 × fi 3 | |
| 1 | 8 | 9 | 10 | 11 | 12 | 13 |
| 17,385 | 1 | 17,385 | 37,88 | – | – | – |
| 20,555 | 4 | 82,220 | 35,64 | – | – | – |
| 23,725 | 8 | 189,800 | 0,27 | – | – | – |
| 26,895 | 3 | 80,685 | 33,77 | 3 | 80,685 | 15,39 |
| 30,065 | 1 | 30,065 | 42,58 | 3 | 90,195 | 2,46 |
| 33,235 | – | – | – | 1 | 33,235 | 16,61 |
| Всего | 17 | 400,155 | 150,14 | 7 | 204,115 | 34,46 |
Значения показателей средней урожайности зерновых культур государственных предприятий, обществ с ограниченной ответственностью и фермерских хозяйств не совпадали со значениями этих же показателей, рассчитанными по формуле 4.18 в примере п. 4.4 (с. 64), что обусловлено разными методиками расчета средних величин. Однако они отражают общую тенденцию соотношения урожайности зерновых культур предприятий различных организационно-правовых форм одного региона и дают точный результат при оценке тесноты связи между факторным и результативным показателями.
Общая дисперсия урожайности по всей совокупности предприятий региона, рассчитанная по формуле 5.7: 15,4.
Дисперсия урожайности (формула 5.7):
Межгрупповая дисперсия, рассчитанная по формуле 5.14: 6,7.
Средняя из внутригрупповых дисперсий, рассчитанная по формуле 5.17: 8,7.
Полученные результаты отвечают правилу сложения дисперсий (формула 5.18):
Для оценки тесноты связи между урожайностью и организационно-правовой формой сельхозпредприятий исчислим эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.
Эмпирический коэффициент детерминации, рассчитанный по формуле 5.19: 0,435.
Эмпирический коэффициент детерминации показывает, что 43,5% вариации урожайности зерновых культур сельхозпредприятий региона обусловлено их организационно-правовой формой.
Эмпирическое корреляционное отношение, рассчитанное по формуле 5.20: 0,66.
Полученное значение свидетельствует о заметной связи между урожайностью зерновых культур сельскохозяйственных предприятий региона и их организационно-правовой формой хозяйствования (см. табл. 5.10).
Показатели дифференциации и концентрации распределения
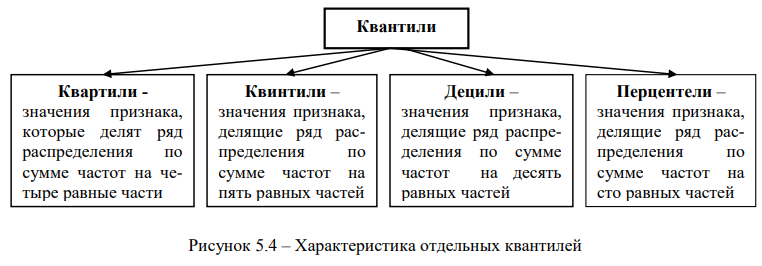
Структуру вариационного ряда характеризуют значения признака, аналогичные медиане, которые называются квантилями или градиентами.
Квантили (градиенты) – это значения признака, которые делят все единицы ряда распределения на равные по численности группы. Частные случаи квантилей приведены на рис. 5.4.
Квантили используются для характеристики степени различия значений уровней признака единиц вариационного ряда, относящихся к выделенным группам. На основании значений квантилей рассчитывают коэффициенты дифференциации: квартильный коэффициент, квинтильный коэффициент, децильный коэффициент, коэффициент фондов, широко используемые при изучении дифференциации доходов населения.
Для расчета квартильного, квинтильного и децильного коэффициентов рассчитываются соответственно первые и последние квартили, квинтили и децили.
Отметим, что второй квартиль (Q2) равен медиане, а первый (Q1) и третий (Q3) квартили исчисляются аналогично расчету медианы, только вместо медианного интервала берется для первого квартиля интервал, в котором находится варианта, отсекающая ¼ численности частот, а для третьего квартиля – варианта, отсекающая ¾ частот.
Первый квартиль (Q1) рассчитывается по формуле:
третий квартиль (Q3) рассчитывается по формуле:
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
iQ – величина интервала (квартильного);
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Пример расчета квартилей
По данным таблицы 4.13, используя данные таблицы 5.5, необходимо рассчитать квартили ряда распределения работников предприятия по уровню заработной платы.
Первый квартиль находится во втором интервале (10000-12000), так как его накопленная частота (100 чел.) равна ¼ численности всех работников предприятия (400 : 4 = 100).
По формуле 5.21: Q1 = 12000 руб., т. е. одна четверть работников предприятия получает заработную плату меньше 12000 руб.
Третий квартиль находится в четвертом интервале (14000-16000), так как его накопленная частота (350 чел.) превышает 3/4 численности всех работников предприятия (400 : 4 × 3 = 300).
По формуле 5.2: Q3 = 14888,89 руб., т. е. три четверти работников предприятия получают заработную плату меньше 14889 руб., одна четверть – больше.
Методика расчета квинтилей, децилей и других квантилей аналогична расчету квартилей.
Пример расчета децилей
По данным таблицы 4.13, используя данные таблицы 5.5, необходимо рассчитать децили ряда распределения работников предприятия по уровню заработной платы.
Первый дециль, величина которого означает, что 10% единиц совокупности имеют значения ниже этого значения, находится во втором интервале (10000-12000), так как его накопленная частота (100 чел.) превышает численности всех работников предприятия (400 : 10 = 40).
Адаптировав формулу 5.21 к нижнему децилю, рассчитаем его значение: d1 = 10500 руб., т. е. 10% работников предприятия получает заработную плату ниже 10500 руб.
Девятый дециль, величина которого означает, что 10% единиц совокупности имеют значения выше этого значения, находится в пятом интервале (16000-19000), так как его накопленная частота (390 чел.) превышает 9/10 численности всех работников предприятия (400 : 10 × 9 = 360).
Адаптировав формулу 5.22 к верхнему децилю, рассчитаем его значение: d9 = 16500 руб., т. е. 10% работников предприятия получает заработную плату выше 16500 руб.
Методики расчета и сущностная характеристика коэффициентов дифференциации приведены в таблице 5.13.
| Название показателя | Формула для расчета | № формулы | Сущностная характеристика |
|---|---|---|---|
| Квартильный коэффициент | KQ = Q3/Q1 | 5.23 | характеризует соотношение между верхним и нижним квартилями и показывает во сколько раз минимальное значение признака в последней четверти единиц совокупности выше максимального значения признака в первой четверти единиц совокупности |
| Децильный коэффициент | Kd = d9/d1 | 5.24 | характеризует соотношение между верхним и нижним децилями |
| Коэффициент фондов (фондовый коэффициент) | Kф = x10 / x1 | 5.25 | определяется как соотношение между средними уровнями значений признака внутри сравниваемых групп, находящихся в разных концах ряда распределения. Он более точно измеряет уровень дифференциации Формула соответствует случаю, если ряд распределения разбит на десять частей, при этом x10 и x1 – соответственно среднее значение признака в десятой и первой частях ряда распределения. |
В статистической практике эти показатели используются в статистике доходов населения (домашних хозяйств) как показатели распределения денежных доходов, характеризующие степень превышения минимального среднедушевого дохода соответствующей квантильной части наиболее обеспеченного населения над максимальным среднедушевым доходом части наименее обеспеченного населения. Например, децильный коэффициент показывает, во сколько раз минимальный среднедушевой денежный доход 10% наиболее обеспеченной части населения превышает максимальный среднедушевой денежный доход 10% наименее обеспеченного населения.
Пример расчета квартильного и децильного коэффициентов
По данным таблицы 4.13 и примеров расчета квартилей и децилей необходимо рассчитать квартильный и децильный коэффициенты.
По формуле 5.23: KQ = 1,24, т.е. минимальное значение заработной платы одной четверти наиболее высокооплачиваемых работников предприятия в 1,24 раза превышает максимальное значение заработной платы одной четверти низкооплачиваемых работников.
По формуле 5.24: Kd = 1,57, т.е. минимальное значение заработной платы 10% наиболее высокооплачиваемых работников предприятия в 1,57 раза превышает максимальное значение заработной платы 10 % работников с наименьшим уровнем оплаты труда на предприятии, что характеризует незначительный разрыв в оплате труда работников предприятия.
Фактические статистические данные, характеризующие распределение совокупного дохода домашних хозяйств Российской Федерации по квантильным группам в зависимости от уровня среднедушевых денежных доходов (в расчете в среднем на члена домохозяйства) в месяц, за 2011-2017 гг. приведены в таблице 5.14.
| Квантильные группы в зависимости от уровня среднедушевых денежных доходов | 2011г. | 2013г. | 2015г. | 2017г. |
|---|---|---|---|---|
| Квинтильные группы: | ||||
| – 1 группа (с наименьшими денежными доходами) | 6617,5 | 7465,3 | 8507,6 | 9224,9 |
| – 2 группа | 11481,3 | 13271,8 | 15030,3 | 15904,1 |
| – 3 группа | 16432,8 | 18762,5 | 21383,2 | 22269,2 |
| – 4 группа | 23622,1 | 26770,7 | 30482,0 | 31352,0 |
| – 5 группа (с наибольшими денежными доходами) | 45362,8 | 51679,4 | 56631,7 | 57907,0 |
| Децильные группы: | ||||
| – 1 группа (с наименьшими денежными доходами) | 4994,3 | 5566,8 | 6426,4 | 7052,1 |
| – 2 группа | 8240,7 | 9363,8 | 10588,8 | 11397,7 |
| – 3 группа | 10369,5 | 11990,9 | 13592,4 | 14491,4 |
| – 4 группа | 12593,0 | 14552,7 | 16468,2 | 17316,7 |
| – 5 группа | 15074,5 | 17206,2 | 19569,5 | 20467,2 |
| – 6 группа | 17791,0 | 20318,7 | 23196,9 | 24071,2 |
| – 7 группа | 21278,7 | 24128,9 | 27758,1 | 28406,0 |
| – 8 группа | 25965,4 | 29412,4 | 33205,9 | 34298,0 |
| – 9 группа | 34038,4 | 37406,1 | 42620,8 | 43856,3 |
| – 10 группа (с наибольшими денежными доходами) | 56687,2 | 65952,6 | 70642,5 | 71957,6 |
| Все домохозяйства | 20703,3 | 23588,7 | 26406,9 | 27331,4 |
Если показатели дифференциации характеризуют степень различия значений признаков единиц совокупности, распределенных в равных по численности группах, то показатели концентрации отражают неравномерность распределения значений признака единиц вариационного ряда в равноинтервальных группах, степень сосредоточения (концентрации) значений признака единиц совокупности в отдельных группах.
Чем выше значения показателей концентрации распределения, тем выше неравномерность распределения единиц совокупности на группы по обусловленному признаку, тем менее однородна по этому признаку исследуемая совокупность.
К показателям концентрации относятся коэффициент концентрации Джини, коэффициент Герфиндаля, коэффициент Розенблюта и др.
Коэффициент концентрации Джини (G) используется для характеристики степени неравномерности распределения значений признака вариационного ряда и рассчитываетсят по формуле:
где pi – накопленная частость (доля) численности единиц совокупности; qi – накопленная доля значений признака i-ой группы, приходящихся на все единицы совокупности. Доля значений признака i-ой группы (di) рассчитывается по формуле:
n – число групп в совокупности.
Коэффициент концентрации Джини может принимать значения от 0 до 1, поэтому результат следует разделить либо на 100, если pi или qi выражены в процентах, либо на 10000, если оба показателя выражены в процентах.
Удаление значения коэффициента Джини от нуля свидетельствует о возрастании степени неравномерности распределения значений признака в вариационном ряду и концентрации значений признака в отдельных группах.
Более простой показатель концентрации – коэффициент Герфиндаля, рассчитываемый на основе данных о доле суммарных значений признаков отдельных групп (выраженных, как правило, абсолютными величинами) в совокупном объеме значений признака.
Коэффициент Герфиндаля (H) рассчитывается по формуле:
где доля значений признака i-ой группы в общем объеме значений признака, т.е. di, рассчитанное по формуле 5.27.
Значение коэффициента Герфиндаля определяется влиянием только доминирующих групп, так как группы с незначительной долей значений признака, которая при возведении в квадрат выражается незначащим числом, ощутимого влияния на значение коэффициента не оказывают. Механизм расчета коэффициента Герфиндаля позволяет выделить доминирующие в совокупности группы как наиболее весомые составляющие значения Н.
Основное достоинство коэффициента Герфиндаля – его высокая чувствительность к изменению в совокупном объеме долей наиболее крупных единиц совокупности, что позволяет отслеживать концентрацию значений признака. Другое достоинство данного коэффициента заключается в том, что он реагирует на число единиц в группе. Однако ее наибольшим значениям придается наибольший вес. Вследствие этого существует опасность преувеличения уровня концентрации.
Поэтому наряду с коэффициентом Герфиндаля целесообразно применять коэффициент Розенблюта, который также характеризует концентрацию, однако расставляет акценты в обратном порядке: наибольший вес придается группам с наименьшими долями.
Коэффициент Розенблюта (KR) рассчитывается по формуле:
где i – номер группы в совокупности;
di – доля i-ой группы в общем объеме совокупности;
n – число групп в совокупности.
Диапазон значений коэффициента Розенблюта 0 ≤ KR ≤ 1. KR = 1 при n = 1 и d1 = 1. В целом коэффициент Розенблюта имеет тенденцию преуменьшать концентрацию в совокупности.
Пример расчета показателй концентрации распределения
По данным таблицы 4.13 следует оценить степень концентрации (или неравномерность) распределения работников предприятия по уровню их заработной платы.
Характеристика неравномерности распределения работников предприятия по уровню их заработной платы и их концентрации в отдельных группах осуществляется на основе расчета коэффициентов Джини, Герфиндаля и Розенблюта
Для расчета коэффициента концентрации Джини построим таблицу 5.15.
| Группы работников по уровню заработной платы, руб. | Середина интервала, руб. (xi) | Число работников, чел. (fi) | Удельный вес (частость) работников, % | Накопленная частость, % (pi) | xi × fi, руб. | di, % | qi, % | pi × qi+1 | pi+1 × qi |
|---|---|---|---|---|---|---|---|---|---|
| 8000-10000 | 9000 | 20 | 5 | 5 | 180000 | 3,4 | 3,4 | — | 85 |
| 10000-12000 | 11000 | 80 | 20 | 25 | 880000 | 16,4 | 19,8 | 99 | 1287 |
| 12000-14000 | 13000 | 160 | 40 | 65 | 2080000 | 38,8 | 58,6 | 1465 | 5128 |
| 14000-16000 | 15000 | 90 | 22,5 | 87,5 | 1350000 | 25,2 | 83,8 | 5447 | 8171 |
| 16000-18000 | 17000 | 40 | 10 | 97,5 | 680000 | 12,7 | 96,5 | 8444 | 9650 |
| 18000 и выше | 19000 | 10 | 2,5 | 100 | 190000 | 3,5 | 100 | 9750 | — |
| Всего | – | 400 | 100,0 | – | 5360000 | 100,0 | – | 25205 | 24321 |
По формуле 5.26, с учетом того, что pi и qi были выражены в процентах, G = (25205 – 24321): 10000 = 0,09, что свидетельствует о достаточно равномерном распределении работников предприятия по уровню заработной платы по выделенным группам и слабой концентрации значений заработной платы в отдельных их них.
Для расчета коэффициентов концентрации Герфиндаля и Розенблюта построим таблицу 5.16.
По формуле 5.28: H = 0,2594.
По формуле 5.29: KR = 0,174.
| Группы работников по уровню заработной платы, руб. | Середина интервала, руб. (xi) | Число работников, чел. (fi) | xi × fi, руб. | di, выраженная в форме коэффициента | di 2 | i | i × di |
|---|---|---|---|---|---|---|---|
| 8000-10000 | 9000 | 20 | 180000 | 0,034 | 0,0012 | 1 | 0,034 |
| 10000-12000 | 11000 | 80 | 880000 | 0,164 | 0,0269 | 2 | 0,328 |
| 12000-14000 | 13000 | 160 | 2080000 | 0388 | 0,1505 | 3 | 1,164 |
| 14000-16000 | 15000 | 90 | 1350000 | 0,252 | 0,0635 | 4 | 1,008 |
| 16000-18000 | 17000 | 40 | 680000 | 0,127 | 0,0161 | 5 | 0,635 |
| 18000 и выше | 19000 | 10 | 190000 | 0,035 | 0,0012 | 6 | 0,21 |
| Всего | – | 400 | 5360000 | 1,000 | 0,2594 | – | 3,379 |
Совместная интерпретация полученных значений коэффициентов Герфиндаля и Розенблюта позволяет сделать вывод об умеренной концентрации значений заработной платы в отдельных группах работников предприятия.
Понятие о закономерностях распределения
Между изменением значений варьирующего признака и их частотами существует определенная зависимость. Как правило, частоты в вариационных рядах с ростом значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются (см. табл. 4.13 и 5.3). Значит, частоты в этих рядах изменяются закономерно в связи с изменением варьирующего признака.
Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы распределения.
Графическое изображение вариационного ряда принимает вид плавной кривой, именуемой кривой распределения.
Примером фактической кривой распределения является полигон распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.
Из математической статистики известно, что при увеличении объема статистической совокупности (Ν → ∞) и одновременном уменьшении интервала группировки (h → 0) полигон либо гистограмма распределения все более и более приближаются к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.
Эмпирические кривые распределения, построенные на основе, как правило, относительно небольшого числа наблюдений (т.е. фактические кривые распределения), очень трудно описать аналитически. Поэтому для выявления статистических закономерностей, сравнения и обобщения различных совокупностей аналогичных данных используются теоретические распределения.
Теоретические распределения – это хорошо изученные в теории распределения, представляющие собой зависимости между плотностями распределения и значениями признака, отражающие закономерности распределения. Они описываются статистическими функциями, параметры которых вычисляются по статистическим характеристикам изучаемой совокупности.
Теоретической кривой распределения называется такая кривая распределения, которая выражает общую закономерность данного типа распределения в чистом виде, исключающем влияние случайных для данного типа закономерностей факторов.
Исследование формы распределения предполагает замену эмпирического распределения известным теоретическим, близким ему по форме. При этом необходимо соблюдать условие: различия между эмпирическим и теоретическим распределением должны быть минимальными. Это означает, что сумма частот эмпирического распределения должна соответствовать сумме частот теоретического распределения. Теоретическое распределение в этом случае является некоторой идеализированной моделью эмпирического распределения, и анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений и определению различий между ними.
В статистической практике наиболее широко используют следующие теоретические распределения:
– биномиальное распределение – для описания распределения дискретного альтернативного признака. Оно представляет собой распределение вероятности исходов события, которые можно оценить как положительные или отрицательные;
– распределение Пуассона – для изучения маловероятных событий в большой серии независимых испытаний (объем совокупностей N ≥ 100, доля единиц, обладающих данным признаком d → 0). Распределение Пуассона обычно применяется в статистическом контроле качества в массовом производстве. Например, при изучении количества бракованных деталей в массовом производстве, числа отказов автоматических линий и т.п.;
– распределение Максвелла применяется при исследовании признака, для которого заранее известно, что распределение имеет положительную асимметрию. Чаще всего распределение Максвелла используется при описании технологических характеристик производственных процессов;
– распределение Стьюдента применяют для описания распределения ошибок в малых выборках (n x – средняя арифметическая ряда;
σ 2 – дисперсия значений изучаемого признака;
σ – среднее квадратическое отклонение изучаемого признака;
π = 3,1415 – постоянное число (отношение длины окружности к ее диаметру);
е = 2,7182 – основание натурального логарифма.
Для конкретного распределения среднее значение признака x и среднее квадратическое отклонение σ являются постоянными величинами.
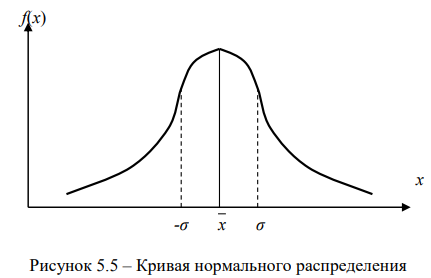
Графически нормальное распределение может быть представлено в виде симметричной колоколообразной кривой, показанной на рис. 5.5.
К основным свойствам кривой нормального распределения относятся:
Этот вывод называется правилом «трех сигм», в соответствии с которым можно считать, что все возможные значения нормально распределенного признака укладываются в интервал x +/- 3σ.
Пользоваться функцией нормального распределения в ее первоначальном виде сложно, так как для каждой пары значений x и σ необходимо создавать свои таблицы значений. Поэтому функцию стандартизируют и затем используют для обработки рядов распределения, для чего вводится понятие стандартного отклонения ti:
Тогда относительная плотность нормального распределения рассчитывается по формуле:
Выражение в скобках состоит из констант, не содержит параметров и называется стандартизированной функцией нормального распределения. Для нее разработаны специальные таблицы, позволяющие находить конкретные значения φ(t)
при различных значениях аргумента ti. Исходная функция нормального распределения связана со стандартизированной соотношением: φ(x) = φ(t) / σ.
Для получения частот теоретического распределения fi т необходимо иметь в виду, что относительная плотность распределения φ(х) связана с одной стороны с частотой fi, а с другой – со стандартизированной функцией нормального распределения φ(t).
где fi т – частота теоретического распределения;
hi – ширина интервала;
N – объем статистической совокупности;
σ – среднее квадратическое отклонение;
φ(t) – стандартизованная функция нормального распределения.
Полученные значения fi т округляют до целых значений в соответствии со смыслом характеристики частоты.
Для определения подобия эмпирического и теоретического распределения, можно построить эмпирическую и теоретическую кривые распределения. Их сопоставление позволяет оценить степень близости и расхождения между ними. Визуальное сопоставление эмпирической и теоретической кривых распределения позволяет получить субъективную оценку их близости.
Для получения объективной оценки близости между эмпирической и теоретической кривыми распределения используются специальные статистические показатели – критерии согласия.
Эмпирическое распределение отличается от теоретического тем, что на значения признака в нем влияют случайные факторы. С увеличением объема статистической совокупности влияние случайных факторов ослабевает, и эмпирическое распределение все менее отличается от теоретического.
Критерии согласия основаны на использовании различных мер расстояний между эмпирическим и теоретическим распределением.
Наиболее часто на практике используются следующие критерии согласия:
где fi и fi т – соответственно, частота эмпирического (фактического) и теоретического распределения; n – количество групп, на которые разбита вся совокупность.
Критерий Пирсона можно использовать при соблюдении таких условий:
где χр 2 – расчетная величина «хи-квадрат»-критерия; n – количество групп, на которые разбита вся совокупность.
Эмпирическое и теоретическое распределение признаются близкими друг другу, если С x =13400 руб., а среднее квадратическое отклонение σ = 2200 руб. Объем исследуемой совокупности N = 400 чел., а ширина интервала hi – 2000 руб.
Для расчета критериев согласия построим таблицу 5.17.
Факт соответствия распределения работников предприятия по уровню их заработной платы нормальному распределению подтверждает то, что сумма частот эмпирического распределения почти равна сумме частот теоретического распределения: Σfi = 400 чел. и Σfi т = 398 чел.
В соответствии с формулой 5.33 расчетное значение «хи-квадрат»-критерия: χр 2 = 8,77.
Для подтверждения оценки близости фактического распределения работников предприятия по уровню заработной платы к нормальному, воспользуемся критерием согласия Романовского, который рассчитывается на основе χ 2 – критерия.
По формуле 5.34 значение критерия согласия Романовского: 2,36.
Так как 2,36 Извлечения из таблицы вероятностей для «лямбда»-критерия согласия
Таким образом, утверждать, что отклонения эмпирических частот от теоретических в рассматриваемом примере являются случайными и что в основе фактического распределения рабочих по уровню заработной платы лежит закон нормального распределения, можно только с вероятностью 46,5%. Расхождения между эмпирическим и теоретическим распределением работников предприятия по уровню заработной платы оказались весьма существенны. Однако значение критерия согласия Романовского дает основание считать, что фактическое распределение работников предприятия по уровню заработной платы близко к нормальному.
Показатели формы распределения
При сравнении эмпирического распределения с нормальным важно констатировать не только согласие этих распределений, но и характер их расхождения. Этому служат показатели формы распределения: показатели асимметрии и эксцесса распределения.
Как отмечалось, нормальное распределение характеризуется симметричностью по отношению к точке, соответствующей значению средней арифметической. Ее вершина находится точно в середине кривой. Поэтому сравнение эмпирического распределения с нормальным, прежде всего, констатирует отсутствие или наличие в нем асимметрии распределения. Асимметричные распределения встречаются чаще, чем симметричные. В асимметричном распределении вершины кривой находятся не в середине, а сдвинуты либо влево, либо вправо. Если вершина сдвинута влево, и, следовательно, правая часть кривой оказывается длиннее левой, то такая асимметрия называется правосторонней. Левосторонней будет асимметрия, когда левая часть кривой длиннее правой, и вершина сдвинута вправо.
Для характеристики асимметрии используют коэффициенты асимметрии.
Коэффициент асимметрии Пирсона (AsП) рассчитывается по формуле:
В симметричных распределениях AsП = 0.
При AsП > 0 наблюдается правостороння асимметрия.
При AsП x > Ме > Мо. При левосторонней асимметрии выполняется неравенство x 0,5, то асимметрия значительна.
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части ряда распределения, поэтому более распространенным и более точным для характеристики ассиметрии распределения является коэффициент асимметрии (As), рассчитанный на основе центрального момента третьего порядка по формуле:
где μ3 – центральный момент третьего порядка, рассчитываемый по формуле 5.43 (табл. 5.18); σ 3 – среднее квадратическое отклонение в третьей степени.
Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины. Средние значения разных степеней отклонений индивидуальных значений признака от его средней арифметической величины получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения. Формулы для расчета центральных моментов первого, второго, третьего и четвертого порядка по несгруппированным и сгруппированным данным, приведены в таблице 5.19.
Величина центрального момента третьего порядка (μ3) зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами и наоборот.
Если в вариационном ряду преобладают варианты, которые больше, чем средняя величина, то Аs > 0, т.е. имеет место правостороння асимметрия.
Если в вариационном ряду преобладают варианты, которые меньше, чем средняя величина, то Аs 4 – среднее квадратическое отклонение в четвертой степени.
Именно отношение μ4 / σ 4 характеризует крутизну (заостренность) графика распределения. Для нормального распределения μ4 / σ 4 = 3, а Ех = 0.
Наличие положительного эксцесса (Ех > 0) означает, что в изучаемой массе явлений существует слабо варьирующее по данному признаку «ядро», окруженное рассеянным «гало», т.е. распределение относится к островершинным, что свидетельствует о концентрации значений признака в центральной группе. При существенном отрицательном эксцессе (Ех Ех ≥ 3, то эксцесс, т.е. отклонение эмпирического распределения от нормального теоретического распределения по вертикали (выше или ниже его вершины), является существенным.
Пример расчета показателей формы распределения
По данным таблицы 4.13 необходимо охарактеризовать форму распределения работников предприятия по уровню их заработной платы, рассчитав коэффициенты асимметрии и эксцесс распределения и построив полигон распределения работников предприятия по уровню их заработной платы.
Значения показателей, характеризующих структуру ряда распределения работников предприятия по уровню заработной платы и ее вариацию, были рассчитаны ранее в соответствующих примерах: X = 13400 руб.; Ме = 13250 руб.; Мо = 13066,67 руб.; σ = 2200 руб.
Так как при сравнении между собой значений средней заработной платы, медианы и моды выполняется неравенство x > Ме > Мо (13400 > 13250 > 13066,67), то ряд распределения работников предприятия по заработной плате является правосторонне асимметричным. Для подтверждения этих выводов найдем коэффициенты асимметрии.
По формуле 5.36 коэффициент асимметрии Пирсона: AsП = 0,15.
As x ) и σ представим в тысячах рублей.
По формуле 5.43 центральный момент третьего порядка: 2,928.
По формуле 5.37 коэффициент асимметрии: 0,27.
Для оценки существенности коэффициента асимметрии, рассчитанного на основе μ3, по формуле 5.46 рассчитаем среднюю квадратическую ошибку коэффициента асимметрии: 0,12.