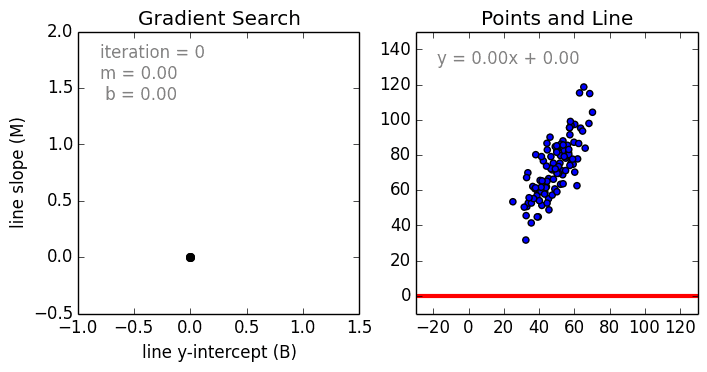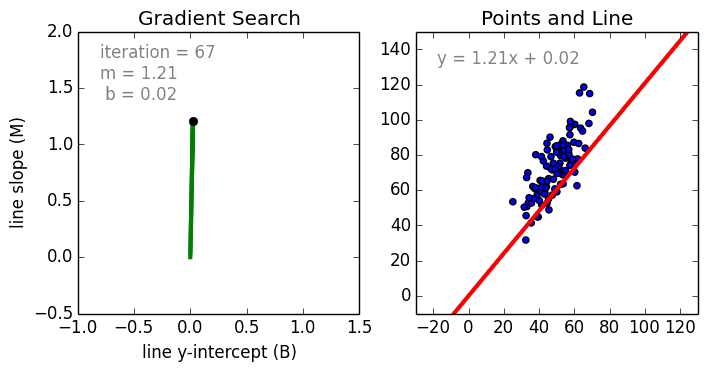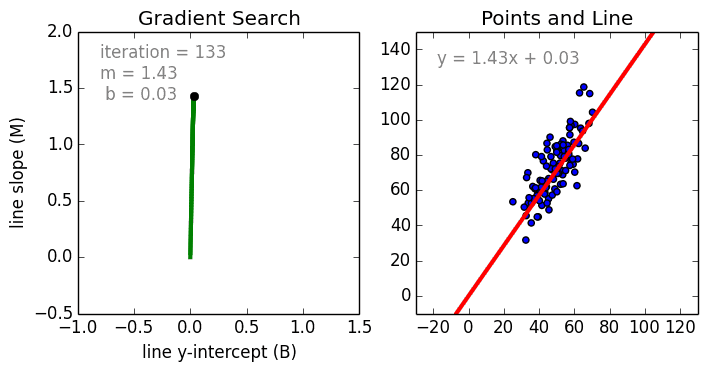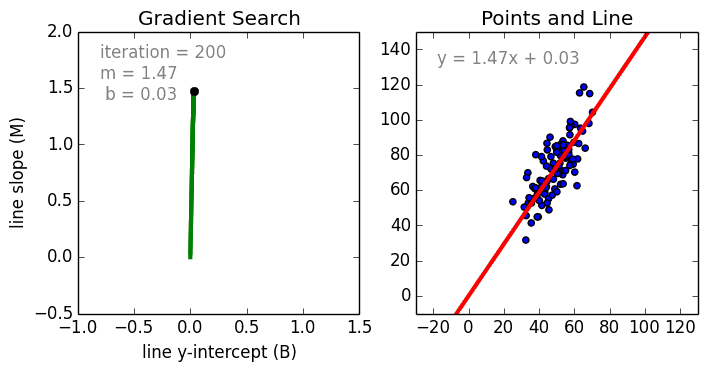
задача регрессии это задача машинного обучения
Регрессия в машинном обучении: оптимальный алгоритм
Регрессия используется в ML. Рассмотрим несколько алгоритмов и определим, как их использовать, исходя из преимуществ и недостатков.
Сталкиваясь с какой-либо проблемой в ML, помните, что есть множество алгоритмов, позволяющих её решить. Однако не существует такого универсального алгоритма, который подходил бы под все случаи и решал абсолютно все проблемы.
Выбор алгоритма строго зависит от размера и структуры ваших данных. Таким образом, выбор правильного алгоритма может быть неясен до тех пор, пока мы не проверим возможные варианты и не наткнёмся на ошибки.
Но каждый алгоритм обладает как преимуществами, так и недостатками, которые можно использовать в качестве руководства для выбора наиболее подходящего под ситуацию.
Линейная и полиномиальная регрессия
Начнём с простого. Одномерная (простая) линейная регрессия – это метод, используемый для моделирования отношений между одной независимой входной переменной (переменной функции) и выходной зависимой переменной. Модель линейная.
Более общий случай – множественная линейная регрессия, где создаётся модель взаимосвязи между несколькими входными переменными и выходной зависимой переменной. Модель остаётся линейной, поскольку выходное значение представляет собой линейную комбинацию входных значений.
Также стоит упомянуть полиномиальную регрессию. Модель становится нелинейной комбинацией входных переменных, т. е. среди них могут быть экспоненциальные переменные: синус, косинус и т. п. Модели регрессии можно обучить с помощью метода стохастического градиента.
Преимущества:
Недостатки:
Нейронные сети
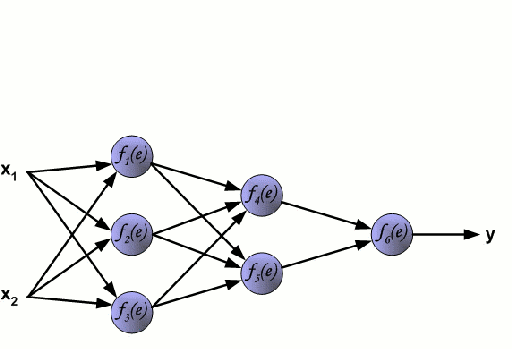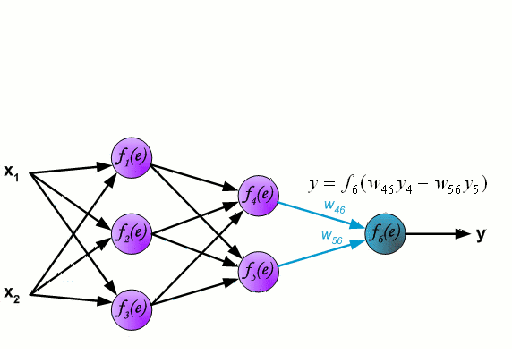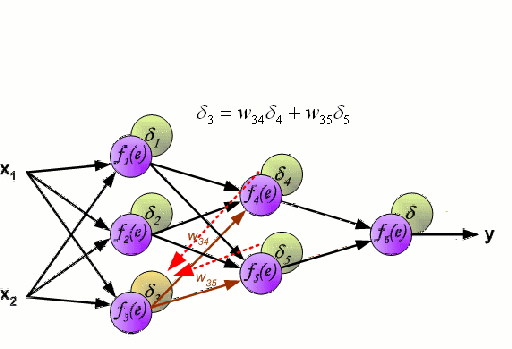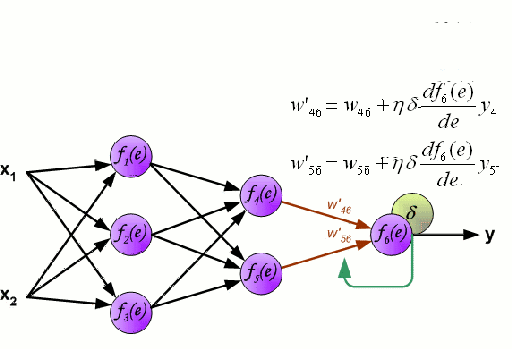
Нейронная сеть состоит из взаимосвязанных групп узлов, называемых нейронами. Входные данные передаются в эти нейроны в виде линейной комбинации со множеством переменных. Значение, умножаемое на каждую функциональную переменную, называется весом. Затем к этой линейной комбинации применяется нелинейность, что даёт нейронной сети возможность моделировать сложные нелинейные отношения. Чаще всего нейросети бывают многослойными: выход одного слоя передается следующему так, как описано выше. На выходе нелинейность не применяется.
Нейронные сети тренируются с помощью метода стохастического градиента и алгоритма обратного распространения ошибки.
Преимущества:
Недостатки:
Дерево принятия решений и Случайный лес
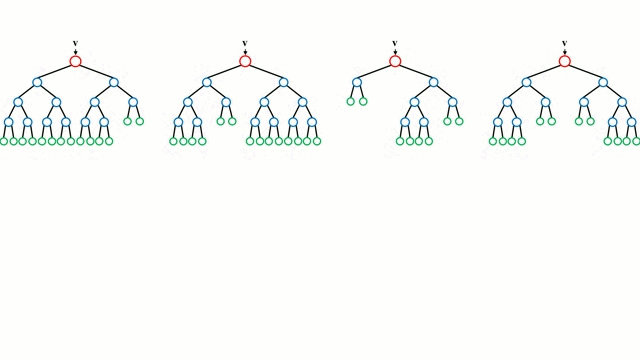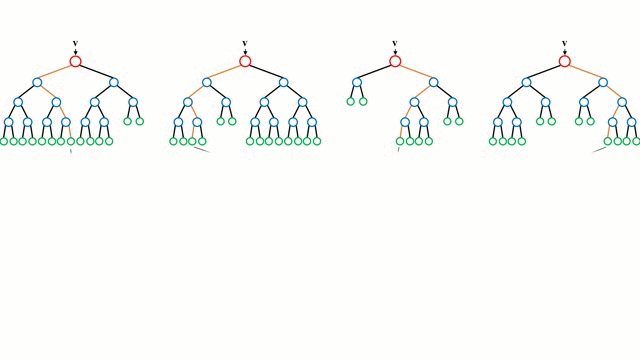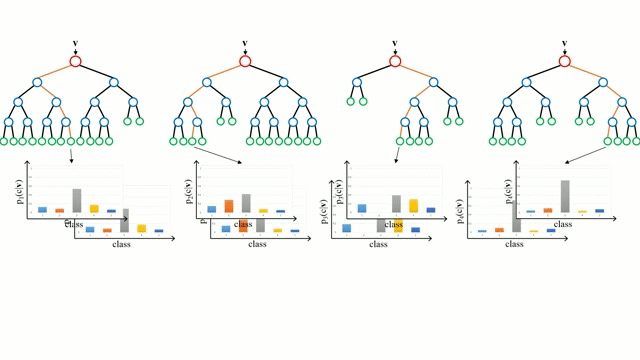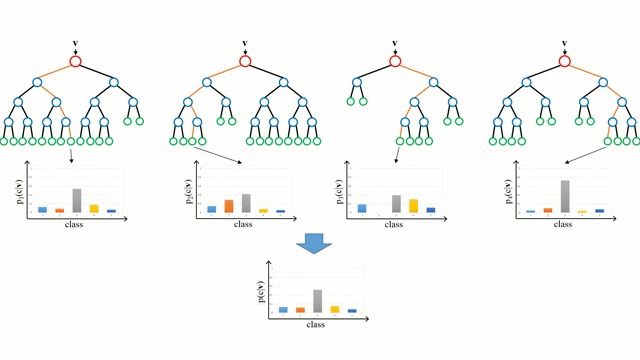
Начнём с простого случая. Дерево принятия решений – это представления правил, находящихся в последовательной, иерархической структуре, где каждому объекту соответствует узел, дающий решение. При построении дерева важно классифицировать атрибуты так, чтобы создать “чистые” узлы. То есть выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов в каждом из этих множеств было как можно меньше.
“Случайные лес” – совокупность деревьев принятия решений. Входной вектор проходит через несколько деревьев решений. Для регрессии выходное значение всех деревьев усредняется; для классификации используется схема голосования для определения конечного класса.
Задачи машинного обучения в ML.NET
Задача машинного обучения — это тип прогноза или вывода, основанный на возникшей проблеме или на вопросе, а также доступных данных. Например, задача классификации назначает данные категориям, а задача кластеризации группирует данные в соответствии со сходством.
Задачи машинного обучения полагаются на шаблоны в данных, а не на явное программирование.
В этой статье описываются разные задачи машинного обучения, которые вы можете выбрать в ML.NET, и распространенные варианты их использования.
Определив задачу для своего сценария, выберите наилучший алгоритм для обучения модели. Далее перечислены доступные алгоритмы для каждой задачи.
Двоичная классификация
Задача контролируемого машинного обучения, которая прогнозирует распределение элементов данных по двум классам (категориям). На вход алгоритма классификации подается набор примеров с метками, каждая из которых представляет собой целое число 0 или 1. Результатом работы алгоритма двоичной классификации является классификатор, который умеет прогнозировать класс для новых экземпляров без метки. Вот несколько примеров для сценария двоичной классификации:
Дополнительные сведения см. в статье о двоичной классификации в Википедии.
Алгоритмы обучения двоичной классификации
Вы можете обучить модель двоичной классификации, используя следующие алгоритмы:
Входные и выходные данные двоичной классификации
Для получения наилучших результатов обучения двоичной классификации обучающие данные должны быть сбалансированы (т. е. число положительных и отрицательных обучающих данных должно быть одинаковым). Отсутствующие значения необходимо обработать до обучения.
Входные данные столбца меток должны иметь тип Boolean. Входные данные столбца функций должны быть вектором Single фиксированного размера.
С помощью этих алгоритмов обучения выводятся следующие столбцы:
Многоклассовая классификация
Задача контролируемого машинного обучения, которая прогнозирует распределение экземпляров данных по нескольким классам (категориям). На вход алгоритма классификации подается набор примеров с метками. Каждая метка обычно запускается как текст. Затем она запускается через TermTransform, который преобразует ее в тип ключа (числовой). Результатом работы алгоритма классификации является классификатор, который умеет прогнозировать класс для новых экземпляров без метки. Вот несколько примеров для сценария многоклассовой классификации:
Дополнительные сведения см. в статье о многоклассовой классификации в Википедии.
В рамках стратегии one-vs.-rest обновляется любой алгоритм обучения двоичной классификации для работы с многоклассовыми наборами данных. Подробнее см. в Википедии.
Алгоритмы обучения многоклассовой классификации
Вы можете обучить модель многоклассовой классификации, используя следующие алгоритмы:
Входные и выходные данные многоклассовой классификации
Входные данные столбца меток должны иметь тип key. Столбец функций должен быть вектором Single фиксированного размера.
Этот алгоритм обучения выводит приведенные ниже данные.
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Вектор Single | Оценки всех классов. Более высокое значение означает большую вероятность попадания в связанный класс. Если i-й элемент имеет самое большое значение, индекс прогнозируемой метки будет равен i. Обратите внимание, что индекс i отсчитывается от нуля. |
| PredictedLabel | Тип key | Индекс прогнозируемой метки. Если его значение равно i, фактическая метка будет i-й категорией во входном типе метки с ключевым значением. |
Регрессия
Задача контролируемого машинного обучения, которая прогнозирует значение метки по набору связанных компонентов. Метка здесь может принимать любое значение, а не просто выбирается из конечного набора значений, как в задачах классификации. Алгоритмы регрессии моделируют зависимость меток от связанных компонентов, чтобы определить закономерности изменения меток при разных значениях компонентов. На вход алгоритма регрессии подается набор примеров с метками известных значений. Результатом работы алгоритма регрессии является функция, которая умеет прогнозировать значения метки для любого нового набора входных компонентов. Вот несколько примеров для сценария регрессии:
Алгоритмы обучения регрессии
Вы можете обучить модель регрессии, используя следующие алгоритмы:
Входные и выходные данные регрессии
Входные данные столбца меток должны иметь тип Single.
Алгоритмы обучения для этой задачи выводят приведенные ниже данные.
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Single | Необработанное оценка, спрогнозированная моделью. |
Кластеризация
Задача неконтролируемого машинного обучения, которая группирует отдельные экземпляры данных в кластеры со сходными характеристиками. Кластеризацию можно также использовать для определения в наборе данных связей, которые невозможно логически отследить просмотром или наблюдением данных. Входные и выходные данные для алгоритма кластеризации зависят от выбранного метода. Вы можете выбрать подход на основе распространения, центроида, возможности подключения или плотности. ML.NET в настоящее время поддерживает только кластеризацию методом К-средних на основе центроида. Примеры сценариев для использования кластеризации:
Алгоритм обучения кластеризации
Вы можете обучить модель кластеризации, используя следующие алгоритмы:
Входные и выходные данные кластеризации
Входные данные функций должны иметь тип Single. Метки не требуются.
Этот алгоритм обучения выводит приведенные ниже данные.
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Вектор Single | Расстояния от указанной точки данных до центроидов всех кластеров. |
| PredictedLabel | Тип key | Индекс ближайшего кластера, спрогнозированный моделью. |
Обнаружение аномалий
Эта задача создает модель обнаружения аномалий с помощью анализа главных компонентов (PCA). Обнаружение аномалий на основе PCA позволяет создавать модели в сценариях, где легко получить данные для обучения из одного класса, такого как допустимые транзакции, однако получить достаточную выборку аномальных значений затруднительно.
Общепринятый метод в машинном обучении, PCA, часто используется в разведочном анализе данных, так как он раскрывает внутреннюю структуру данных и объясняет их вариативность. PCA выполняется путем анализа данных с несколькими переменными. Он выполняет поиск корреляции между переменными и определяет сочетание значений, которые лучше всего фиксируют различия результатов. Эти объединенные значения компонентов используются для создания более компактных компонентов, называемых главными компонентами.
Обнаружение аномалий включает в себя ряд важных задач машинного обучения:
Так как аномалии по определению довольно-таки редкие события, со сборкой репрезентативной выборки данных, используемых для моделирования, могут быть трудности. Алгоритмы, включенные в эту категорию, специально разработаны для решения основных проблем разработки и обучения моделей с использованием несбалансированных наборов данных.
Алгоритм обучения обнаружению аномалий
Вы можете обучить модель обнаружения аномалий, используя следующие алгоритмы:
Входные и выходные данные обнаружения аномалий
Входные данные функций должны быть вектором Single фиксированного размера.
Этот алгоритм обучения выводит приведенные ниже данные.
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Single | Неотрицательная неограниченная оценка, вычисленная моделью обнаружения аномалий |
| PredictedLabel | Boolean | Значение true/false, указывающее, являются ли входные данные аномалией (PredictedLabel=true) или нет (PredictedLabel=false) |
Ранжирование
Задача ранжирования создает средство ранжирования на основе набора примеров с метками. Этот набор примеров состоит из групп экземпляров, которые могут быть оценены с заданными критериями. Метки ранжирования для каждого экземпляра — < 0, 1, 2, 3, 4 >. Средство ранжирования обучается ранжировать новые группы экземпляров с неизвестными оценками для каждого экземпляра. Алгоритмы обучения ранжированию ML.NET основаны на ранжировании машинного обучения.
Алгоритмы обучения ранжированию
Вы можете обучить модель ранжирования, используя следующие алгоритмы:
Входные и выходные данные ранжирования
Входные данные метки должны иметь тип key или Single. Значение метки определяет релевантность, где более высокие значения означают более высокую степень релевантности. Если метка имеет тип key, индексом ключа будет значение релевантности, где наименьший индекс является минимально релевантным. Если метка имеет тип Single, более высокие значения означают более высокую степень релевантности.
Данные должны быть вектором Single фиксированного размера, а входной столбец группы строк должен иметь тип key.
Этот алгоритм обучения выводит приведенные ниже данные.
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Single | Неограниченная оценка, вычисленная моделью для определения прогноза |
Рекомендация
Задача рекомендации позволяет создать список рекомендуемых продуктов или служб. ML.NET использует факторизацию матрицы (MF), алгоритм совместной фильтрации для рекомендаций при наличии исторических данных о рейтинге продуктов в вашем каталоге. Например, у вас есть исторические данные о рейтинге фильмов для ваших пользователей, и вы хотите рекомендовать другие фильмы, которые они, вероятно, просмотрят следующими.
Алгоритмы обучения рекомендациям
Вы можете обучить модель рекомендаций, используя следующий алгоритм:
Прогнозирование
Задача прогнозирования использует предыдущие данные временных рядов, чтобы делать прогнозы о будущем поведении. Сценарии, применимые к прогнозированию, включают прогнозы погоды, прогнозы сезонных продаж и прогнозное обслуживание.
Алгоритмы обучения для прогнозирования
Вы можете обучить модель прогнозирования, используя следующий алгоритм.
Классификация изображений
Задача контролируемого машинного обучения, которая прогнозирует распределение изображений по нескольким классам (категориям). Входные данные — это набор помеченных примеров. Каждая метка обычно запускается как текст. Затем она запускается через TermTransform, который преобразует ее в тип ключа (числовой). Результатом работы алгоритма классификации изображений является классификатор, который можно использовать для прогнозирования класса новых изображений. Задача классификации изображений — это тип классификации по нескольким классам. Вот несколько примеров для сценария классификации изображений:
Алгоритмы обучения классификации изображений
Вы можете обучить модель классификации изображений, используя следующие алгоритмы обучения:
Входные и выходные данные классификации изображений
Входные данные столбца меток должны иметь тип key. Столбец функции должен быть вектором с переменным размером Byte.
Этот алгоритм обучения выводит следующие столбцы:
| Имя выходных данных | Type | Описание |
|---|---|---|
| Score | Single | Оценки всех классов. Более высокое значение означает большую вероятность попадания в связанный класс. Если i-й элемент имеет самое большое значение, индекс прогнозируемой метки будет равен i. Обратите внимание, что индекс i отсчитывается от нуля. |
| PredictedLabel | Тип key | Индекс прогнозируемой метки. Если его значение равно i, фактическая метка будет i-й категорией во входном типе метки с ключевым значением. |
Обнаружение объектов
Задача контролируемого машинного обучения, которая используется для прогнозирования класса (категории) изображения, а также предоставляет ограничивающий прямоугольник для категории внутри изображения. Вместо классификации одного объекта в изображении, обнаружение объектов может определить несколько объектов в изображении. Примеры обнаружения объектов:
Обучение модели обнаружения объектов в настоящее время доступно только в Model Builder с помощью Машинного обучения Azure.
Разница между классификацией и регрессией в машинном обучении
Дата публикации 2017-12-11
Существует важное различие между проблемами классификации и регрессии.
Я часто вижу такие вопросы, как:
Как рассчитать точность для моей проблемы регрессии?
Подобные вопросы являются признаком неправильного понимания разницы между классификацией и регрессией и того, какую точность пытаются измерить.
В этом уроке вы обнаружите различия между классификацией и регрессией.
После завершения этого урока вы узнаете:
Обзор учебника
Этот урок состоит из 5 частей; они есть:
Функция приближения
Подробнее о прогнозирующем моделировании читайте в посте:
Прогнозирующее моделирование может быть описано как математическая проблема приближения функции отображения (f) от входных переменных (X) к выходным переменным (y). Это называется проблемой приближения функций.
Задача алгоритма моделирования состоит в том, чтобы найти лучшую функцию отображения, которую мы можем, учитывая время и ресурсы.
Подробнее об аппроксимирующих функциях в прикладном машинном обучении читайте в посте:
Как правило, мы можем разделить все задачи приближения функций на задачи классификации и задачи регрессии.
Классификация прогнозирующего моделирования
Выходные переменные часто называют метками или категориями. Функция отображения предсказывает класс или категорию для данного наблюдения.
Например, электронное письмо с текстом может быть классифицировано как принадлежащее одному из двух классов: «спам»«а также «не спам«.
Для классификационных моделей характерно предсказывать непрерывное значение как вероятность данного примера, принадлежащего каждому выходному классу. Вероятности могут быть интерпретированы как вероятность или достоверность данного примера, принадлежащего каждому классу. Прогнозируемая вероятность может быть преобразована в значение класса путем выбора метки класса, которая имеет наибольшую вероятность.
Например, конкретному текстовому электронному письму могут быть присвоены вероятности 0,1 как «спама» и 0,9 как «не спама». Мы можем преобразовать эти вероятности в метку класса, выбрав метку «не спам», поскольку она имеет наибольшую прогнозируемую вероятность.
Существует много способов оценить мастерство модели прогнозирования классификации, но, возможно, наиболее распространенным является расчет точности классификации.
Например, если модель прогнозирования классификации сделала 5 прогнозов и 3 из них были правильными, а 2 из них были неправильными, то точность классификации модели, основанной только на этих прогнозах, была бы:
Алгоритм, способный изучать модель прогнозирования классификации, называется алгоритмом классификации.
Прогнозирующее регрессионное моделирование
Например, можно предположить, что дом будет продаваться по определенной долларовой стоимости, возможно, в диапазоне от 100 000 до 200 000 долларов.
Поскольку прогнозирующая модель регрессии предсказывает количество, навык модели должен быть указан как ошибка в этих прогнозах.
Есть много способов оценить мастерство модели прогнозирования регрессии, но, возможно, наиболее распространенным является вычисление среднеквадратичной ошибки, сокращенно обозначаемой как RMSE.
Преимущество RMSE состоит в том, что единицы оценки ошибки находятся в тех же единицах, что и прогнозируемое значение.
Алгоритм, который способен изучать модель прогнозирования регрессии, называется алгоритмом регрессии.
Некоторые алгоритмы имеют в своем названии слово «регрессия», например, линейная регрессия и логистическая регрессия, что может привести к путанице, поскольку линейная регрессия является алгоритмом регрессии, тогда как логистическая регрессия является алгоритмом классификации.
Классификация против регрессии
Классификация задач прогнозного моделирования отличается от задач регрессионного прогнозного моделирования.
Существует некоторое совпадение между алгоритмами классификации и регрессии; например:
Некоторые алгоритмы могут использоваться как для классификации, так и для регрессии с небольшими модификациями, такими как деревья решений и искусственные нейронные сети. Некоторые алгоритмы не могут или не могут быть легко использованы для обоих типов задач, таких как линейная регрессия для прогнозирующего моделирования регрессии и логистическая регрессия для прогнозного моделирования классификации.
Важно отметить, что способ, которым мы оцениваем прогнозы классификации и регрессии, варьируется и не перекрывается, например:
Преобразование между проблемами классификации и регрессии
В некоторых случаях можно преобразовать проблему регрессии в задачу классификации. Например, прогнозируемое количество может быть преобразовано в отдельные сегменты.
Это часто называется дискретизацией, а результирующая выходная переменная представляет собой классификацию, в которой метки имеют упорядоченное отношение (называемое порядковым номером).
В некоторых случаях проблема классификации может быть преобразована в проблему регрессии. Например, метка может быть преобразована в непрерывный диапазон.
Некоторые алгоритмы уже делают это, предсказывая вероятность для каждого класса, которая, в свою очередь, может быть масштабирована до определенного диапазона:
Кроме того, значения классов могут быть упорядочены и сопоставлены с непрерывным диапазоном:
Если метки классов в задаче классификации не имеют естественного порядкового отношения, преобразование из классификации в регрессию может привести к удивительной или плохой производительности, поскольку модель может узнать ложное или несуществующее отображение из входных данных в непрерывный выходной диапазон.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.
Резюме
В этом уроке вы обнаружили разницу между проблемами классификации и регрессии.
В частности, вы узнали:
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
5 алгоритмов регрессии в машинном обучении, о которых вам следует знать
Быстренько назовите пять алгоритмов машинного обучения. Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты.
Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.
Перевели статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.
1. Нейросетевая регрессия
Теория. Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.
Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).
Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.
Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.
Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.
Реализация. Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).
Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.
Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.
2. Регрессия дерева решений
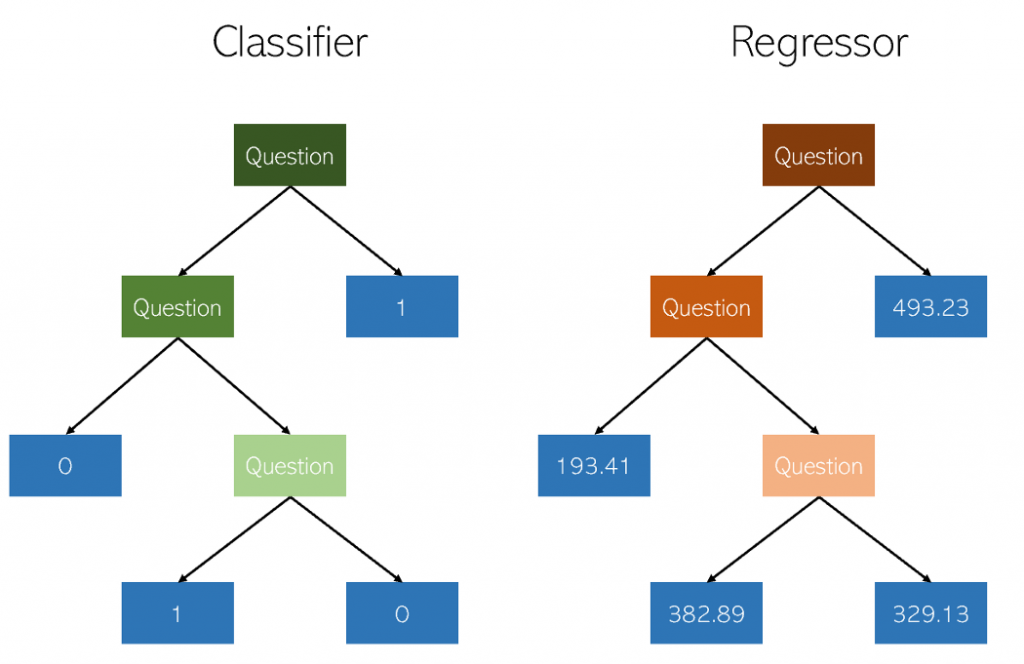
Теория. Деревья решений в классификации и регрессии очень похожи, поскольку работают путем построения деревьев с узлами «да/нет». Однако в то время как конечные узлы классификации приводят к одному значению класса (например, 1 или 0 для задачи бинарной классификации), деревья регрессии заканчиваются значением в непрерывном режиме (например, 4593,49 или 10,98).
Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.
Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.
Реализация. Регрессия дерева решений может быть легко создана в sklearn:
Поскольку параметры регрессора дерева решений очень важны, рекомендуется использовать инструмент оптимизации поиска параметров GridCV из sklearn, чтобы найти правильные рекомендации для этой модели.
При формальной оценке производительности используйте тестирование K-fold вместо стандартного train-test-split, чтобы избежать случайности последнего, которая может нарушить чувствительные результаты модели с высокой дисперсией.
Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.
3. Регрессия LASSO
Теория. Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).
Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).
Иллюстрация автора. Упрощенная визуализация процесса сжатия
Процесс сжатия добавляет регрессионным моделям несколько преимуществ:
Вместо того чтобы корректировать сложность модели, компенсируя сложность данных, подобно методам регрессии с высокой дисперсией нейронных сетей и дерева решений, лассо пытается уменьшить сложность данных так, чтобы их можно было обрабатывать простыми методами регрессии, искривляя пространство, на котором они лежат. В этом процессе лассо автоматически помогает устранить или исказить сильно коррелированные и избыточные функции в методе с низкой дисперсией.
Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.
Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.
Реализация. В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.
4. Гребневая регрессия (ридж-регрессия)
Теория. Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).
Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.
Сравнение ошибок в регрессии лассо (слева) и гребневой регрессии (справа). Поскольку гребневая регрессия использует регуляризацию L2, ее площадь напоминает круг, тогда как регуляризация лассо L1 рисует прямые линии. Свободное изображение. Источник
В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.
Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.
Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.
Реализация. Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.