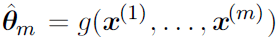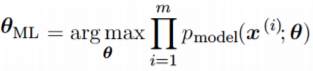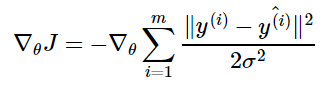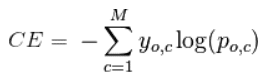задачи бинарной классификации в машинном обучении

Обзор методов классификации в машинном обучении с помощью Scikit-Learn

Авторизуйтесь

Обзор методов классификации в машинном обучении с помощью Scikit-Learn

Для машинного обучения на Python написано очень много библиотек. Сегодня мы рассмотрим одну из самых популярных — Scikit-Learn.

Scikit-Learn упрощает процесс создания классификатора и помогает более чётко выделить концепции машинного обучения, реализуя их с помощью понятной, хорошо документированной и надёжной библиотекой.

Что такое Scikit-Learn?

Scikit-Learn — это Python-библиотека, впервые разработанная David Cournapeau в 2007 году. В этой библиотеке находится большое количество алгоритмов для задач, связанных с классификацией и машинным обучением в целом.

Scikit-Learn базируется на библиотеке SciPy, которую нужно установить перед началом работы.

Основные термины

В системах машинного обучения или же системах нейросетей существуют входы и выходы. То, что подаётся на входы, принято называть признаками (англ. features).

Признаки по существу являются тем же, что и переменные в научном эксперименте — они характеризуют какой-либо наблюдаемый феномен и их можно как-то количественно измерить.

Когда признаки подаются на входы системы машинного обучения, эта система пытается найти совпадения, заметить закономерность между признаками. На выходе генерируется результат этой работы.

Этот результат принято называть меткой (англ. label), поскольку у выходов есть некая пометка, выданная им системой, т. е. предположение (прогноз) о том, в какую категорию попадает выход после классификации.

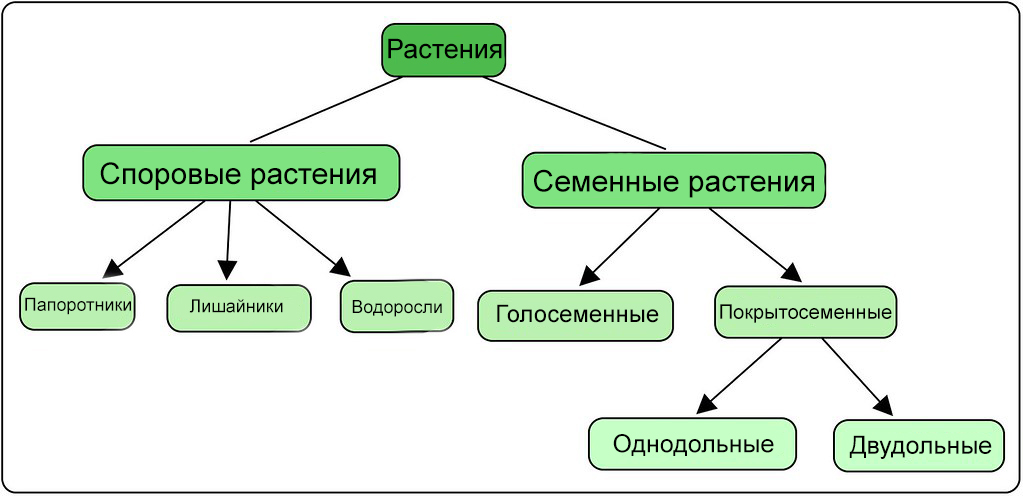
В контексте машинного обучения классификация относится к обучению с учителем. Такой тип обучения подразумевает, что данные, подаваемые на входы системы, уже помечены, а важная часть признаков уже разделена на отдельные категории или классы. Поэтому сеть уже знает, какая часть входов важна, а какую часть можно самостоятельно проверить. Пример классификации — сортировка различных растений на группы, например «папоротники» и «покрытосеменные». Подобная задача может быть выполнена с помощью Дерева Решений — одного из типов классификатора в Scikit-Learn.

При обучении без учителя в систему подаются непомеченные данные, и она должна попытаться сама разделить эти данные на категории. Так как классификация относится к типу обучения с учителем, способ обучения без учителя в этой статье рассматриваться не будет.

Процесс обучения модели — это подача данных для нейросети, которая в результате должна вывести определённые шаблоны для данных. В процессе обучения модели с учителем на вход подаются признаки и метки, а при прогнозировании на вход классификатора подаются только признаки.

Принимаемые сетью данные делятся на две группы: набор данных для обучения и набор для тестирования. Не стоит проверять сеть на том же наборе данных, на которых она обучалась, т. к. модель уже будет «заточена» под этот набор.

Типы классификаторов

Scikit-Learn даёт доступ ко множеству различных алгоритмов классификации. Вот основные из них:

На сайте Scikit-Learn есть много литературы на тему этих алгоритмов с кратким пояснением работы каждого из них.

Метод k-ближайших соседей (K-Nearest Neighbors)

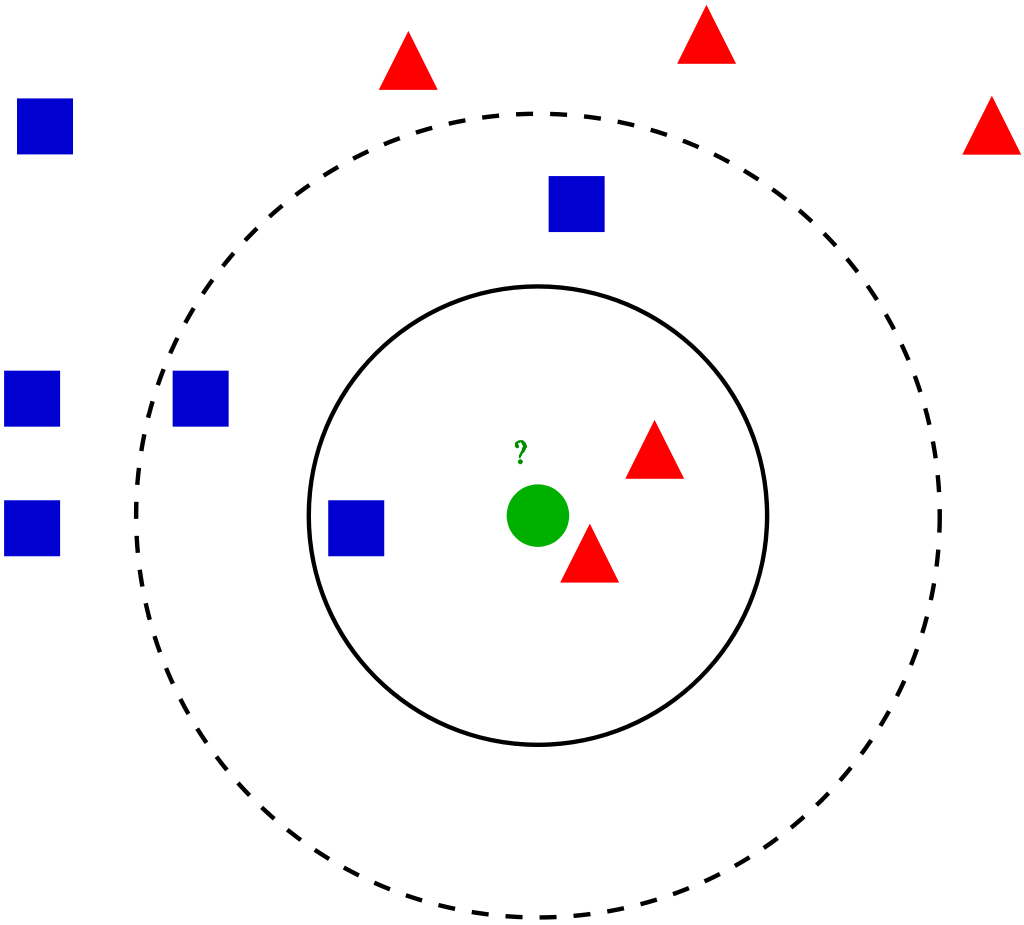
Этот метод работает с помощью поиска кратчайшей дистанции между тестируемым объектом и ближайшими к нему классифицированным объектами из обучающего набора. Классифицируемый объект будет относится к тому классу, к которому принадлежит ближайший объект набора.

Классификатор дерева решений (Decision Tree Classifier)

Этот классификатор разбивает данные на всё меньшие и меньшие подмножества на основе разных критериев, т. е. у каждого подмножества своя сортирующая категория. С каждым разделением количество объектов определённого критерия уменьшается.

Классификация подойдёт к концу, когда сеть дойдёт до подмножества только с одним объектом. Если объединить несколько подобных деревьев решений, то получится так называемый Случайный Лес (англ. Random Forest).

Наивный байесовский классификатор (Naive Bayes)

Такой классификатор вычисляет вероятность принадлежности объекта к какому-то классу. Эта вероятность вычисляется из шанса, что какое-то событие произойдёт, с опорой на уже на произошедшие события.

Каждый параметр классифицируемого объекта считается независимым от других параметров.

Линейный дискриминантный анализ (Linear Discriminant Analysis)

Этот метод работает путём уменьшения размерности набора данных, проецируя все точки данных на линию. Потом он комбинирует эти точки в классы, базируясь на их расстоянии от центральной точки.

Этот метод, как можно уже догадаться, относится к линейным алгоритмам классификации, т. е. он хорошо подходит для данных с линейной зависимостью.

Метод опорных векторов (Support Vector Machines)

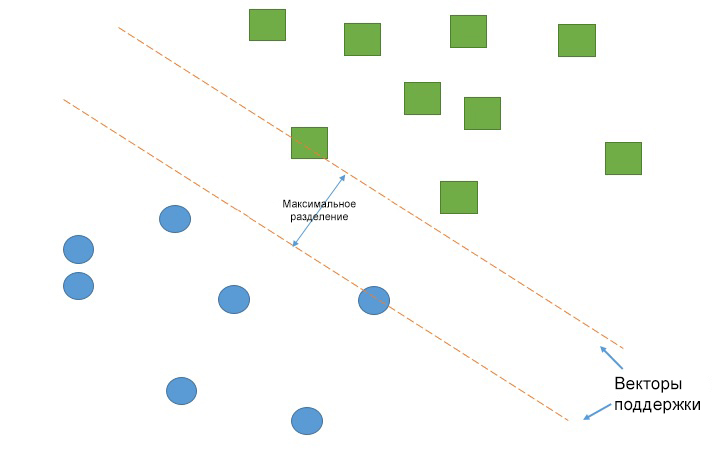
Работа метода опорных векторов заключается в рисовании линии между разными кластерами точек, которые нужно сгруппировать в классы. С одной стороны линии будут точки, принадлежащие одному классу, с другой стороны — к другому классу.

Классификатор будет пытаться увеличить расстояние между рисуемыми линиями и точками на разных сторонах, чтобы увеличить свою «уверенность» определения класса. Когда все точки построены, сторона, на которую они падают — это класс, которому эти точки принадлежат.

Логистическая регрессия (Logistic Regression)

У каждого признака есть своя метка, равная только 0 или только 1. Логистическая регрессия является линейным классификатором и поэтому используется, когда в данных прослеживается какая-то линейная зависимость.

Примеры задач классификации

Задача классификации — эта любая задача, где нужно определить тип объекта из двух и более существующих классов. Такие задачи могут быть разными: определение, кошка на изображении или собака, или определение качества вина на основе его кислотности и содержания алкоголя.

В зависимости от задачи классификации вы будете использовать разные типы классификаторов. Например, если классификация содержит какую-то бинарную логику, то к ней лучше всего подойдёт логистическая регрессия.

По мере накопления опыта вам будет проще выбирать подходящий тип классификатора. Однако хорошей практикой является реализация нескольких подходящих классификаторов и выбор наиболее оптимального и производительного.

Реализация классификатора

Первый шаг в реализации классификатора — его импорт в Python. Вот как это выглядит для логистической регрессии:

Вот импорты остальных классификаторов, рассмотренных выше:

Однако, это не все классификаторы, которые есть в Scikit-Learn. Про остальные можно прочитать на соответствующей странице в документации.

После этого нужно создать экземпляр классификатора. Сделать это можно создав переменную и вызвав функцию, связанную с классификатором.

Теперь классификатор нужно обучить. Перед этим нужно «подогнать» его под тренировочные данные.

Обучающие признаки и метки помещаются в классификатор через функцию fit :

Эти этапы (создание экземпляра, обучение и классификация) являются основными при работе с классификаторами в Scikit-Learn. Но эта библиотека может управлять не только классификаторами, но и самими данными. Чтобы разобраться в том, как данные и классификатор работают вместе над задачей классификации, нужно разобраться в процессах машинного обучения в целом.

Процесс машинного обучения

Процесс содержит в себе следующие этапы: подготовка данных, создание обучающих наборов, создание классификатора, обучение классификатора, составление прогнозов, оценка производительности классификатора и настройка параметров.

Во-первых, нужно подготовить набор данных для классификатора — преобразовать данные в корректную для классификации форму и обработать любые аномалии в этих данных. Отсутствие значений в данных либо любые другие отклонения — все их нужно обработать, иначе они могут негативно влиять на производительность классификатора. Этот этап называется предварительной обработкой данных (англ. data preprocessing).

Следующим шагом будет разделение данных на обучающие и тестовые наборы. Для этого в Scikit-Learn существует отличная функция traintestsplit.

Как уже было сказано выше, классификатор должен быть создан и обучен на тренировочном наборе данных. После этих шагов модель уже может делать прогнозы. Сравнивая показания классификатора с фактически известными данными, можно делать вывод о точности классификатора.

Вероятнее всего, вам нужно будет «корректировать» параметры классификатора, пока вы не достигните желаемой точности (т. к. маловероятно, что классификатор будет соответствовать всем вашим требованиям с первого же запуска).

Ниже будет представлен пример работы машинного обучения от обработки данных и до оценки.

Реализация образца классификации

Поскольку набор данных iris достаточно распространён, в Scikit-Learn он уже присутствует, достаточно лишь заложить эту команду:

Тем не менее, тут ещё нужно подгрузить CSV-файл, который можно скачать здесь.

Благодаря тому, что данные уже были подготовлены, долгой предварительной обработки они не требуют. Единственное, что может понадобиться — убрать ненужные столбцы (например ID ) таким образом:

Теперь нужно определить признаки и метки. С библиотекой Pandas можно легко «нарезать» таблицу и выбрать определённые строки/столбцы с помощью функции iloc() :

Код выше выбирает каждую строку и столбец, обрезав при этом последний столбец.

Выбрать признаки интересующего вас набора данных можно также передав в скобках заголовки столбцов:

После того, как вы выбрали нужные признаки и метки, их можно разделить на тренировочные и тестовые наборы, используя функцию train_test_split() :

Чтобы убедиться в правильности обработки данных, используйте:

Теперь можно создавать экземпляр классификатора, например метод опорных векторов и метод k-ближайших соседей:

Теперь нужно обучить эти два классификатора:

Эти команды обучили модели и теперь классификаторы могут делать прогнозы и сохранять результат в какую-либо переменную.

Теперь пришло время оценить точности классификатора. Существует несколько способов это сделать.

Нужно передать показания прогноза относительно фактически верных меток, значения которых были сохранены ранее.

Вот, к примеру, результат полученных метрик:

Поначалу кажется, что KNN работает точнее. Вот матрица неточностей для SVC:

Количество правильных прогнозов идёт с верхнего левого угла в нижний правый. Вот для сравнения метрики классификации для KNN:

Оценка классификатора

Когда дело доходит до оценки точности классификатора, есть несколько вариантов.

Точность классификации

Точность классификации измерять проще всего, и поэтому этот параметр чаще всего используется. Значение точности — это число правильных прогнозов, делённое на число всех прогнозов или, проще говоря, отношение правильных прогнозов ко всем.

Хоть этот показатель и может быстро дать вам явное представление о производительности классификатора, его лучше использовать, когда каждый класс имеет хотя бы примерно одинаковое количество примеров. Так как такое будет случаться редко, рекомендуется использовать другие показатели классификации.

Логарифмические потери

Значение Логарифмических Потерь (англ. Logarithmic Loss) — или просто логлосс — показывает, насколько классификатор «уверен» в своём прогнозе. Логлосс возвращает вероятность принадлежности объекта к тому или иному классу, суммируя их, чтобы дать общее представление об «уверенности» классификатора.

Этот показатель лежит в промежутке от 0 до 1 — «совсем не уверен» и «полностью уверен» соответственно. Логлосс сильно падает, когда классификатор сильно «уверен» в неправильном ответе.

Площадь ROC-кривой (AUC)

Такой показатель используется только при бинарной классификации. Площадь под ROC-кривой представляет способность классификатора различать подходящие и не подходящие какому-либо классу объекты.

Значение 1.0 : вся область, попадающая под кривую, представляет собой идеальный классификатор. Следовательно, 0.5 означает, что точность классификатора соответствует случайности. Кривая рассчитывается с учётом точности и специфичности модели. Подробнее о расчётах можно прочитать здесь.

Матрица неточностей

Матрица неточностей (англ. Confusion Matrix) — это таблица или диаграмма, показывающая точность прогнозирования классификатора в отношении двух и более классов. Прогнозы классификатора находятся на оси X, а результат (точность) — на оси Y.

Ячейки таблицы заполняются количеством прогнозов классификатора. Правильные прогнозы идут по диагонали от верхнего левого угла в нижний правый. Про это можно почитать в данной статье.

Отчёт о классификации

В библиотеке Scikit-Learn уже встроена возможность создавать отчёты о производительности классификатора. Эти отчёты дают интуитивно понятное представление о работе модели.

Заключение

Чтобы лучше вникнуть в работу с Scikit-Learn, неплохо было бы узнать больше о работе различных методов классификации. После этого стоит лучше узнать о замере производительности классификаторов. Однако понимание многих нюансов в классификации приходит только со временем.

Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.

Перейти к регистрации

Источник

Классификация

Материал из MachineLearning.

Классификация — один из разделов машинного обучения, посвященный решению следующей задачи. Имеется множество объектов (ситуаций), разделённых некоторым образом на классы. Задано конечное множество объектов, для которых известно, к каким классам они относятся. Это множество называется обучающей выборкой. Классовая принадлежность остальных объектов не известна. Требуется построить алгоритм, способный классифицировать произвольный объект из исходного множества.

Классифицировать объект — значит, указать номер (или наименование класса), к которому относится данный объект.

Классификация объекта — номер или наименование класса, выдаваемый алгоритмом классификации в результате его применения к данному конкретному объекту.

В математической статистике задачи классификации называются также задачами дискриминантного анализа.

В машинном обучении задача классификации относится к разделу обучения с учителем. Существует также обучение без учителя, когда разделение объектов обучающей выборки на классы не задаётся, и требуется классифицировать объекты только на основе их сходства друг с другом. В этом случае принято говорить о задачах кластеризации или таксономии, и классы называть, соответственно, кластерами или таксонами.

Содержание

Типология задач классификации

Типы входных данных

Классификацию сигналов и изображений называют также распознаванием образов.

Типы классов

Классификация: формальная постановка

Вероятностная постановка задачи

Признаковое пространство

В зависимости от множества признаки делятся на следующие типы:

Часто встречаются прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.

Примеры прикладных задач

Задачи медицинской диагностики

В роли объектов выступают пациенты. Признаки характеризуют результаты обследований, симптомы заболевания и применявшиеся методы лечения. Примеры бинарных признаков: пол, наличие головной боли, слабости. Порядковый признак — тяжесть состояния (удовлетворительное, средней тяжести, тяжёлое, крайне тяжёлое). Количественные признаки — возраст, пульс, артериальное давление, содержание гемоглобина в крови, доза препарата. Признаковое описание пациента является, по сути дела, формализованной историей болезни. Накопив достаточное количество прецедентов в электронном виде, можно решать различные задачи:

Ценность такого рода систем в том, что они способны мгновенно анализировать и обобщать огромное количество прецедентов — возможность, недоступная специалисту-врачу.

Предсказание месторождений полезных ископаемых

Признаками являются данные геологической разведки. Наличие или отсутствие тех или иных пород на территории района кодируется бинарными признаками. Физико-химические свойства этих пород могут описываться как количественными, так и качественными признаками. Обучающая выборка составляется из прецедентов двух классов: районов известных месторождений и похожих районов, в которых интересующее ископаемое обнаружено не было. При поиске редких полезных ископаемых количество объектов может оказаться намного меньше, чем количество признаков. В этой ситуации плохо работают классические статистические методы. Задача решается путём поиска закономерностей в имеющемся массиве данных. В процессе решения выделяются короткие наборы признаков, обладающие наибольшей информативностью — способностью наилучшим образом разделять классы. По аналогии с медицинской задачей, можно сказать, что отыскиваются «синдромы» месторождений. Это важный побочный результат исследования, представляющий значительный интерес для геофизиков и геологов.

Оценивание кредитоспособности заёмщиков

Эта задача решается банками при выдаче кредитов. Потребность в автоматизации процедуры выдачи кредитов впервые возникла в период бума кредитных карт 60-70-х годов в США и других развитых странах. Объектами в данном случае являются физические или юридические лица, претендующие на получение кредита. В случае физических лиц признаковое описание состоит из анкеты, которую заполняет сам заёмщик, и, возможно, дополнительной информации, которую банк собирает о нём из собственных источников. Примеры бинарных признаков: пол, наличие телефона. Номинальные признаки — место проживания, профессия, работодатель. Порядковые признаки — образование, занимаемая должность. Количественные признаки — сумма кредита, возраст, стаж работы, доход семьи, размер задолженностей в других банках. Обучающая выборка составляется из заёмщиков с известной кредитной историей. В простейшем случае принятие решений сводится к классификации заёмщиков на два класса: «хороших» и «плохих». Кредиты выдаются только заёмщикам первого класса. В более сложном случае оценивается суммарное число баллов (score) заёмщика, набранных по совокупности информативных признаков. Чем выше оценка, тем более надёжным считается заёмщик. Отсюда и название — кредитный скоринг. На стадии обучения производится синтез и отбор информативных признаков и определяется, сколько баллов назначать за каждый признак, чтобы риск принимаемых решений был минимален. Следующая задача — решить, на каких условиях выдавать кредит: определить процентную ставку, срок погашения, и прочие параметры кредитного договора. Эта задача также может быть решения методами обучения по прецедентам.

Источник

Функции оценки, потерь, оптимизации – основы алгоритма Машинного Обучения

Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.

Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.

Функции оценки

В контексте технологии машинного обучения, оценка – это статистический термин для нахождения некоторого приближения неизвестного параметра на основе некоторых данных. Точечная оценка – это попытка найти единственное лучшее приближение некоторого количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений, предположительно близкое к оцениваемому параметру.

Под количеством интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной регрессии
• Целая функция

Точечная оценка

Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.

Точечная оценка также может относиться к оценке взаимосвязи между входными и целевыми переменными, в этом случае чаще называемой функцией оценки.

Функция оценки

Задача, решаемая машинным обучением, заключается в попытке предсказать переменную y по заданному входному вектору x. Мы предполагаем, что существует функция f(x), которая описывает приблизительную связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает часть y, которая явно не предсказывается входным вектором x. При оценке функций нас интересует приближение f с помощью модели или оценки fˆ. Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.

Смещение и дисперсия

Смещение и дисперсия измеряют два разных источника ошибки функции оценки. Смещение измеряет ожидаемое отклонение от истинного значения функции или параметра. Дисперсия, с другой стороны, показывает меру отклонения от ожидаемого значения оценки, которую может вызвать любая конкретная выборка данных.

Смещение

Смещение определяется следующим образом:

где ожидаемое значение E(θˆ_m) для данных (рассматриваемых как выборки из случайной величины) и θ является истинным базовым значением, используемым для определения распределения, генерирующего данные.

Оценщик θˆ_m называется несмещенным, если bias(θˆ_m)=0, что подразумевает что E(θˆ_m) = θ.

Дисперсия и Стандартная ошибка

Дисперсия оценки обозначается как Var(θˆ), где случайная величина является обучающим множеством. Альтернативно, квадратный корень дисперсии называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет изменяться по мере того, как мы меняем выборки из базового набора данных, генерирующих процесс.

Точно так же, как мы хотели бы, чтобы функция оценки имела малое смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.

Давайте теперь рассмотрим некоторые обычно используемые функции оценки.

Оценка Максимального Правдоподобия (MLE)

Оценка максимального правдоподобия может быть определена как метод оценки параметров (таких как среднее значение или дисперсия) из выборки данных, так что вероятность получения наблюдаемых данных максимальна.

Оценка максимального правдоподобия для θ определяется как:

Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше уравнение можно записать в виде:

Эта произведение многих вероятностей может быть неудобным по ряду причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это произведение членов, нам нужно применить правило цепочки, которое довольно громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации, можно использовать логарифм вероятности, который не меняет его argmax, но удобно превращает произведение в сумму, и поскольку логарифм – строго возрастающая функция (функция натурального логарифма – монотонное преобразование), это не повлияет на итоговое значение θ.

Два важных свойства: сходимость и эффективность

Сходимость. По мере того, как число обучающих выборок приближается к бесконечности, оценка максимального правдоподобия сходится к истинному значению параметра.

Эффективность. Способ измерения того, насколько мы близки к истинному параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной разницы между оценочными и истинными значениями параметров, где математическое ожидание вычисляется над m обучающими выборками из данных, генерирующих распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с увеличением m, и для больших m нижняя граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.

Именно по причине сходимости и эффективности, оценка максимального правдоподобия часто считается предпочтительным оценщиком для машинного обучения.

Когда количество примеров достаточно мало, чтобы привести к переобучению, стратегии регуляризации, такие как понижающие веса, могут использоваться для получения смещенной версии оценки максимального правдоподобия, которая имеет меньшую дисперсию, когда данные обучения ограничены.

Максимальная апостериорная (MAP) оценка

Согласно байесовскому подходу, можно учесть влияние предварительных данных на выбор точечной оценки. MAP может использоваться для получения точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка MAP выбирает точку максимальной апостериорной вероятности (или максимальной плотности вероятности в более распространенном случае непрерывного θ):

где с правой стороны, log(p(x|θ)) – стандартный член логарифмической вероятности и log(p(θ)) соответствует изначальному распределению.

Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.

Функции потерь

В большинстве обучающих сетей ошибка рассчитывается как разница между фактическим выходным значением y и прогнозируемым выходным значением ŷ. Функция, используемая для вычисления этой ошибки, известна как функция потерь, также часто называемая функцией ошибки или затрат.

До сих пор наше основное внимание уделялось оценке параметров с помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в том, что и MLE, и MAP предоставляют механизм для получения функции потерь.

Давайте рассмотрим некоторые часто используемые функции потерь.

Средняя квадратичная ошибка (MSE): средняя квадратичная ошибка является наиболее распространенной функцией потерь. Функция потерь MSE широко используется в линейной регрессии в качестве показателя эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными значениями и истинными, возвести ее в квадрат и усреднить по всему набору данных.

где y (i) – фактический ожидаемый результат, а ŷ (i) – прогноз модели.

Многие функции потерь (затрат), используемые в машинном обучении, включая MSE, могут быть получены из метода максимального правдоподобия.

Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP, требуется некоторая математика. Вы можете пропустить ее и перейти к следующему разделу.

Получение MSE из MLE

Можно смоделировать модель линейной регрессии следующим образом:

мы предполагаем, что у имеет нормальное распределение с ŷ в качестве среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное распределения являются разумным выбором во многих случаях. В отсутствие предварительных данных о том, какое распределение в действительности соответствует рассматриваемым данным, нормальное распределение является хорошим выбором по умолчанию.

Вернемся к логарифмической вероятности, определенной ранее:

где ŷ(i) – результат линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим, что две первые величины являются постоянными, поэтому максимизация логарифмической вероятности сводится к минимизации MSE:

Таким образом, максимизация логарифмического правдоподобия относительно θ дает такую же оценку параметров θ, что и минимизация среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое расположение оптимума. Это оправдывает использование MSE в качестве функции оценки максимального правдоподобия.

Кросс-энтропия (или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными распределениями. Если кросс-энтропия велика, это означает, что разница между двумя распределениями велика, а если кросс-энтропия мала, то распределения похожи друг на друга.

Кросс-энтропия определяется как:

где P – распределение истинных ответов, а Q – распределение вероятностей прогнозов модели. Можно показать, что функция кросс-энтропии также получается из MLE, но я не буду утомлять вас большим количеством математики.

Давайте еще упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака, кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели

Бинарная классификация

В случае бинарной классификации (M=2), формула имеет вид:

При двоичной классификации каждая предсказанная вероятность сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка, которая штрафует вероятность на основе расстояния от ожидаемого значения.

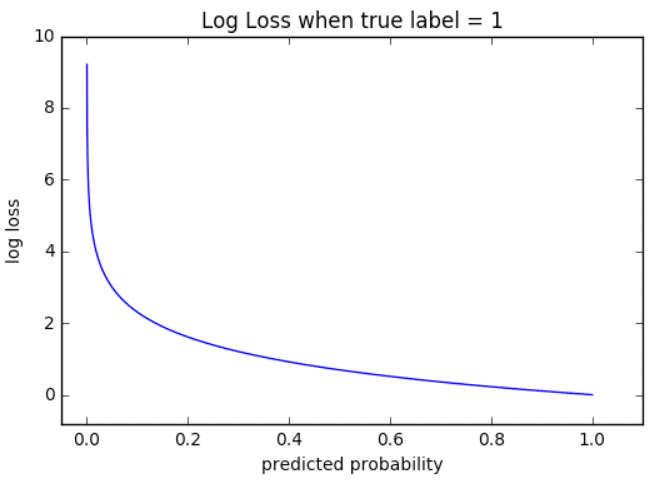
Визуализация

На приведенном ниже графике показан диапазон возможных значений логистической функции потерь с учетом истинного наблюдения (y = 1). Когда прогнозируемая вероятность приближается к 1, логистическая функция потерь медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.

Логистическая функция потерь наказывает оба типа ошибок, но особенно те прогнозы, которые являются достоверными и ошибочными!

Мульти-классовая классификация

В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для каждого прогноза наблюдаемых классов.

Кросс-энтропия для бинарной или двух-классовой задачи прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех примеров. Log loss использует отрицательные значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход основан на том, что логарифм чисел

Задача бинарной классификации

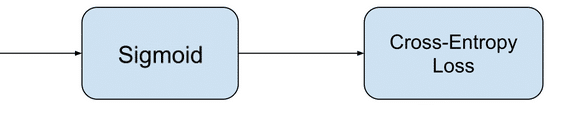
Задача состоит в том, чтобы классифицировать пример как принадлежащий одному из двух классов. Или более точно, задача сформулирована как предсказание вероятности того, что пример принадлежит первому классу, например, классу, которому вы присваиваете целочисленное значение 1, тогда как другому классу присваивается значение 0.

• Конфигурация выходного уровня: один узел с сигмовидной активационной функцией.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Задача мульти-классовой классификации

Эта задача состоит в том, чтобы классифицировать пример как принадлежащий одному из нескольких классов. Задача сформулирована как предсказание вероятности того, что пример принадлежит каждому классу.

• Конфигурация выходного уровня: один узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Рассмотрев оценку и различные функции потерь, давайте перейдем к роли оптимизаторов в алгоритмах ML.

Оптимизаторы

Чтобы свести к минимуму ошибку или потерю в прогнозировании, модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты ошибок строятся в зависимости от W и также описываются графиком функции затрат J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация ошибки также часто называется минимизацией функции затрат.

Но как именно это делается? Используя оптимизаторы.

Оптимизаторы используются для обновления весов и смещений, то есть внутренних параметров модели, чтобы уменьшить ошибку.

Самым важным методом и основой того, как мы обучаем и оптимизируем нашу модель, является метод Градиентного Спуска.

Градиентный Спуск

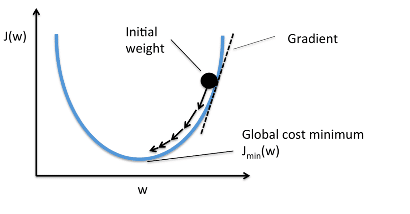
Когда мы строим функцию затрат J(w), это можно представить следующим образом:

Как видно из кривой, существует значение параметров W, которое имеет минимальное значение J_min. Нам нужно найти способ достичь этого минимального значения.

В алгоритме градиентного спуска мы начинаем со случайных параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая обновлять параметры, чтобы приблизиться к минимальным значениям.

Повторяем до достижения минимума:

В приведенном выше уравнении мы обновляем параметры модели после каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на каждой итерации.

Градиент функции затрат вычисляется как частная производная функции затрат J по каждому параметру модели W_j, где j принимает значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения, поэтому общее время, затрачиваемое моделью для достижения минимума, будет больше.

Есть три способа сделать градиентный спуск:

Пакетный градиентный спуск: использует все обучающие данные для обновления параметров модели в каждой итерации.

Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.

Вот некоторые другие часто используемые Оптимизаторы:

Стохастический Градиентный Спуск (SGD): обновляет параметры, используя только один обучающий параметр на каждой итерации. Такой параметр обычно выбирается случайным образом. Стохастический градиентный спуск часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч обучающих или более параметров, поскольку он будет сходиться быстрее, чем пакетный градиентный спуск.

Адаград

Адаград адаптирует скорость обучения конкретно к индивидуальным особенностям: это означает, что некоторые веса в вашем наборе данных будут отличаться от других. Это работает очень хорошо для разреженных наборов данных, где пропущено много входных значений. Однако, у Адаграда есть одна серьезная проблема: адаптивная скорость обучения со временем становится очень маленькой.

Некоторые другие оптимизаторы, описанные ниже, пытаются справиться с этой проблемой.

RMSprop

RMSprop – это специальная версия Adagrad, разработанная профессором Джеффри Хинтоном в его классе нейронных сетей. Вместо того, чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается решить некоторые проблемы, которые Адаград оставляет открытыми.

Адам означает адаптивную оценку момента и является еще одним способом использования предыдущих градиентов для вычисления текущих градиентов. Адам также использует концепцию импульса, добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил довольно широкое распространение и практически принят для использования в обучающих нейронных сетях.

Вы только что ознакомились с кратким обзором оптимизаторов. Более подробно об этом можно прочитать здесь.

Я надеюсь, что после прочтения этой статьи, вы будете лучше понимать что происходит, когда Вы пишите следующий код:

Спасибо за проявленный интерес!

Источник