задачный подход в обучении

Дидактор

педагогическая практика

Сущность задачного подхода в обучении

Если ничто другое не помогает,
попробуй действовать по инструкции!

Педагоги давно пришли к выводу, что на современном уроке «передача знаний» не является главной целью. Более того, такая организация урока, где детям выдаются готовые рафинированные знания, губи­тельна для познавательной деятельности.

Ученик должен быть поставлен в условия поиска, заблуждений, радостных открытий и огорчений от временных неудач. Мышление начинается там, где есть неизвестное, где встречаются затруднение, непонима­ние, ошибка. А, следовательно, учитель так продумывает урок, что поставленные учебные цели подразделяются на ряд учебных задач, решаемых учащимися совместно или самостоятельно.

Еще великий Сократ отмечал, что

«учитель – не тот, кто дает, а тот, у кого берут».

Система запланированных целей неразрывно связана с системой действий, которые ведут к выполнению этих целей. Тем, что вызывает эти активные действия, становятся учебные задачи, выступающие как разновидность опережающего управления познавательной деятельностью, «проект будущего учебного действия», определяющий интеллектуальное пространство, в котором ученик станет выполнять мыслительные операции.

Несмотря на большие изменения в российском образовании, по-прежнему наиболее традиционным является «знаниевый» подход в обучении. Суть его заключается в том, чтобы передать учащимся необходимый объем знаний. Единица обучения — порция знаний, т. е. предметной информации, в которой ученики должны осознать значение и смысл.

«Знаниевый» подход развивает почти исключительно интеллектуальную сферу сознания, причем только ту ее часть, которая связана с памятью, совершенно не затрагивая волевую, эмоционально-чувственную и мотивационную сферы сознания обучаемых. Преобладание «знаниевой» подготовки над всеми остальными видами обучения приводит к развитию формального уровня образования.

Такая подготовка затрудняет переход от обучения в образовательном учреждении к многообразной жизнедеятельности выпускника школы.
Относительно недавно сформировался «задачный» подход, который основной акцент делает на разрешение в ходе обучения различных учебных задач, вопросов, ситуаций и т. д. Единица такого обучения — интеллектуальное умение (или даже навык), позволяющее разрешать учебные задачи, давать ответы на вопросы.

«Задачный» подход интенсивно развивает интеллектуальную сферу сознания, но в отличие от «знаниевого» — прежде всего, логическое мышление.

Специально организованное, правильно и систематически осуществляемое обучение в виде разрешения разнообразных учебных задач расширяет возможности обучения.

Развивается ориентировочная сторона учебной деятельности, когда ученик активно занимается поиском правильного решения, самостоятельно добывает новые знания. Кроме того, возрастает роль аналитико-поисковой деятельности по определению последствий учебных действий, сокращается набор «проб» и «ошибок», появляется стремление найти все возможные для данной задачи решения, возрастает вариативность действий.

При этом существенно развиваются волевая и мотивационная сферы учебной деятельности и в некоторой степени эмоционально-чувственная.

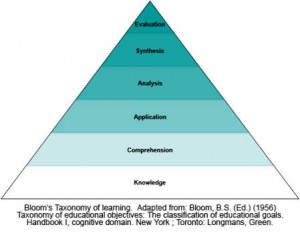
Имеющиеся таксономии учебных целей, и особенно таксономия Б. Блума, широко используются в образовательных технологиях при построении системы типовых задач для определения конкретных умений учащихся. М.Е. Бершадский и М.Е. Гузеев приводят конкретный пример заданий для школьников из различных предметных областей, по результатам которых можно судить о различных уровнях обученности.

Примеры задач для различных уровней учебных целей

в познавательной области по Бенджамину Блуму.

Знание.

Понимание.

Применение.

Анализ.

Синтез.

Оценка.

(Б.Е. Бершадский, В.В. Гузеев. Дидактические и психологические основания образовательной технологии. М.,2003. С. 144-146.)

Отнесение большинства описанных учебных задач к определенному уровню обученности не вызывает сомнения, что, по замечанию цитируемых авторов, «и является необходимым критерием применимости таксономии для разработки системы мониторинга».

В то же время некоторые из заданий, к примеру, на применение можно было бы отнести к уровню анализа или даже оценки. Во всяком случае, создатели различных образовательных технологий, как правило, стремятся к разработке собственных таксономий учебных задач.

При всем разнообразии подходов привлекает внимание стремление специалистов с помощью таксономии проследить весь учебный процесс, создать систему учебного мониторинга не только для определения достижений учащихся, но и динамики всего учебного процесса.

Одной из наиболее популярных является разработка известного чешского ученого Даны Толлингеровой, которая, опираясь на таксономию учебных целей Б. Блума, предложила таксономию учебных задач, разделенных на 5 категорий, содержащих 27 типов учебных задач по операционной структуре, то есть по операциям, необходимым для их выполнения.

Полнота и детальная разработанность таксономии учебных задач, а также то обстоятельство, что задания в ней упорядочены по когнитивной сложности и сопоставлены с количественным показателем (тип задач), позволяет использовать эту таксономию не только как оценочную шкалу, но и для разработки алгоритма учебных действий.

ТАКСОНОМИЯ УЧЕБНЫХ ЗАДАЧ ПО Д. ТОЛЛИНГЕРОВОЙ

1. Задачи, требующие мнемического воспроизведения данных:

2. Задачи, требующие простых мыслительных операций с данными:

3. Задачи, требующие сложных мыслительных операций с данными:

4. Задачи, требующие сообщения данных:

5. Задачи, требующие творческого мышления.

К первой категории относятся задачи, требующие от уча­щегося мнемических операций, содержание которых преду­сматривает узнавание операций, содержание которых предусмат­ривает узнавание или репродукцию отдельных фактов или их целого. Чаще всего они начинаются со слов:

Во вторую категорию включены задачи, при решении ко­торых уже необходимы элементарные операции. Это задачи по выявлению, перечислению, сопоставлению, обобщению и т.п. Начинаются они обычно словами:

Третья категория охватывает задачи, решение которых требует сложных мыслительных операций.

Сюда относятся задачи по индукции, дедукции, интерпретации, верификации и др. Начинаются они обычно со слов:

Следует указать, что к этой категории относятся все задачи, в которых учащиеся должны перевести что-то с одного «языка» на другой, например, выразить формулу, прочитать что-либо, перевести текст с родного языка на иностранный и т.д.

В четвертую категорию включены задачи, предусматри­вающие для их решения помимо мыслительных операций еще какой-нибудь речевой акт, устный или письменный. Следователь­но, сюда относятся все задачи, требующие не только проведение определенных операций, но и высказываний о них. Учащийся в этих задачах дает показание не только о результате решения, но также и о его ходе, условиях, фазах, компонентах, трудностях и т.д.

В пятую категорию входят задачи, которые предполагают самостоятельность при решении задач. Начинаются они обычно словами:

Это уже задачи, которые предполагают не только знание всех предшест­вующих операций, но и способность комбинировать их в большие блоки, структуры, секвенции, стратегии и пр. так, чтобы они создавали нечто новое, пусть даже только субъектно, то есть для учащегося, новое.

Дидактическая ценность системы учебных задач, по мнению Д.Толлингеровой, связана с выполнением поставленной педагогической цели:

При этом, сравнительно разнородный набор задач, где чередуются разные познавательные операции, предотвращает демотивацию учащихся под влиянием монотонности задаваемых задач.

Как видим, все задачи, предложенные Д. Толлингеровой, проранжированы по возрастанию когнитивной сложности и операциональной ценности. Система запланированных целей неразрывно связана с системой действий, которые ведут к выполнению этих целей.

Тем, что вызывает эти активные действия, становятся учебные задачи, выступающие как разновидность опережающего управления когнитивной деятельностью, «проект будущего учебного действия», определяющий интеллектуальное пространство, в котором ученик станет выполнять мыслительные действия.

Таким образом, с использованием таксономии можно конструировать систему учебных задач для выполнения поставленных педагогических целей, более полно учитывать состав когнитивных требований к учебной ситуации, проводить диагностику знаний и уровня сформированности учебных действий учащихся, а также прогнозировать ход обучения с учетом меры сложности задач и степени нагрузки на все виды проектируемой познавательной деятельности, то есть можно создавать индивидуальную программу развития обучаемых или более эффективно организовывать дифференцированную работу.

По мнению Д.Толлингеровой, главная задача учителя — научиться составлять учебные задачи так, чтобы их операционная структура соответствовала преследуемым педагогическим целям и учебному материалу:

«Если анализ учебного материала ведет к определению того, что учащийся в конце обучения будет знать, то анализ учебных действий ведет к определению того, что учащийся с усваиваемыми познаниями должен сделать — определить их, сопоставить, дедуцировать, применять и т.д.»

Таксономия учебных задач.

Русский язык. 3 класс. (Программа 1-4). Составлено учительницей начальных классов средней школы №6 г. Армавира АСТВАЦАТУРОВОЙ Т.П.

Тема: Род имен существительных. Изменение имен существительных по числам и падежам.

I. Задания первого уровня направлены на развитие памя­ти и формирование репродуктивных знаний.

1. Слова, которые обозначают предметы и отвечают на вопросы _______ или __________ называются ____________

2. Существительные бывают _____________ и ______________ рода

3. Существительные изменяются по _____________ и по________________. В единственном числе по _________________

4. Сколько падежей в русском языке? _______

5. Вставь пропущенные буквы:

6. Вставь подходящие по смыслу имена существительные, чтобы получился рассказ про зайца.

У него длинные ___________, короткий _____ и косые ___________

Маленький ____ всего боится.

Слова для справок: зайчик, уши, глаза, хвост, лес, мор­ковь, капуста, животное, кора, зверек.

II. Задания второго уровня направлены на умение транс­формировать репродуктивные знания.

2. Данные имена существительные напиши во множествен­ном числе:

в единственном числе:

Подчеркни правильное утверждение:

4. Просклоняй существительное весна. Выдели окончания.
И. _____________________

5. Укажи падеж выделенных существительных:

Каждое утро мы ходим в школу ( ). В школе ( ) мы уз-тем много нового. Володя сидит за первой партой ( ). Он положил на парту ( ) свои книги.

III. Задания направлены на усвоение мыслительных опе­раций и формирование продуктивных знаний.

1. Подчеркни существительные, которые употребляются только во множественном числе:

столы, штаны, санки, машины, клещи, ножницы, молоко.

2. Знаешь ли ты, как будет множественное число от слов:
человек-

3. Прочитай и образуй новые слова:
Москва — москвич — москвичка.

Укажи род записанных существительных.

4. В каких падежах использовал поэт существительные, создавая свой зимний пейзаж?

На сосне (…) и на березе (…) — бахрома (…). Белой пряжей (…) их запутала зима (…). И оставила распутывать весне (…) Эту пряжу на березе (…) и сосне (…).

Какой падеж отсутствует?

5. Замени одним словом:

Человек, который играет на трубе — ______________

Человек, который выступает в цирке- _______________

Край земли у воды — ____________________

Комментарии к “ Сущность задачного подхода в обучении ”

На уроках английского языка мы также сопоставляем и применяем наши знания на практике. Например: Вставьте предлоги: 1. John is looking ____ a job.
a for
b after
c to

2. Is it the photograph ____ your brother?
a of
b with
c to

интересно и полезно. всё выстраивается в понятную систему, есть желание многое поменять в построении своих уроков. спасибо

Очень интересно попробую применить на занятиях по логопедии.

Спасибо большое автору. Нашла ответы на свои вопросы.

Источник

Презентация на тему «Задачный подход как условие организации учебной деятельности»

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Задачный подход как условие организации учебной деятельности

Формирующее оценивание направлено на решение трех задач: формирование контрольно-оценочной самостоятельности учащихся грамотное разворачивание учебной деятельности в коллективных, коллективно-индивидуальных формах улучшение обучения

Для решения всех задач формирующего оценивания необходимо ввести учебное сотрудничество «Учитель-группа совместно действующих детей». Важно регулярно- использовать такую форму работы на уроках

Ученикам необходимо изменить поведение от пассивных получателей знаний, на активных, которые управляют своим собственным обучением. Именно такому поведению должен способствовать задачный подход в обучении, где учащиеся проявляют поисковую активность.

тема урока: Eco-helpers Тема: Eco-helper

Грамотно организованная учебная деятельность в задачном подходе помогает формированию у школьников учебной самостоятельности.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Специфика преподавания английского языка с учетом требований ФГОС

Курс повышения квалификации

Актуальные вопросы преподавания английского языка в условиях реализации ФГОС

Номер материала: ДБ-1507163

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В Москве стартует онлайн-чемпионат для школьников Soft Skills — 2035

Время чтения: 1 минута

Гинцбург анонсировал регистрацию детской вакцины от COVID-19

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

Новый ГОСТ на окна с защитой для детей вступает в силу 1 ноября

Время чтения: 1 минута

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Время чтения: 1 минута

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Тема выступления: «Личностно-ориентированное обучение в учебно- воспитательном процессе. Задачный подход».

Ищем педагогов в команду «Инфоурок»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 12 города Ельца

Выступление на педагогическом совете.

Тема педагогического совета: «Воспитательная функция школы в современных условиях образования».

Тема выступления : «Личностно-ориентированное обучение в учебно-

С 90-х годов прошлого века понятие « личностно-ориентированное обучение» прочно вошло в учебно-воспитательный процесс школы. Надо сказать, что это понятие неново для нашей отечественной педагогики. Ещё Константин Дмитриевич Ушинский говорил о том, что обучение должно быть обращено к личности ученика. И только тогда можно ожидать положительных результатов в обучении и воспитании. Стоит вспомнить 70-е годы прошлого века, когда школьное образование было нацелено на воспитание всесторонне развитой личности.

Впервые вопрос о технологиях личностно-ориентированного обучения рассматривался в работах И.С.Якиминской.

Несомненно, личностно-ориентированное обучение нельзя отождествлять с индивидуальным подходом, т. к. такое обучение направлено, в целом, на перевод ученика с позиции объекта учебно-воспитательного процесса на позицию субъекта. А это означает смену парадигмы образования, основными направлениями которой становятся гуманизация и гуманитаризация учебно-воспитательного процесса.

« Гуманизация процесса предполагает усиление внимания к формированию личности человека. Психологами ( В.В.Давыдов,В.В.Репкин и др.) и методистами (А.М.Пышкало, О.Б.Епищева и др.) показано, что задачи развития и воспитания личности могут быть эффективно решены путём формирования учебной деятельности. Она становится той основой, на которой происходит становление личности.»(с.199, М.А.Гончарова).

«Гуманитаризация образования направлена на формирование личностной зрелости обучаемых. Она призвана создавать условия, побуждающие школьника к активной творческой деятельности и обеспечивать его участие в ней» ( с.203, М.А. Гончарова «Основные направления образования» Вестник,2008).

Подчеркнём, что всё это в той или иной степени нашло своё отражение в стандартах второго поколения, в которых чётко прописаны цели обучения: 1) в направлении личностного развития, 2) в метапредметном направлении, 3) в предметном направлении.

С задачами мы сталкиваемся не только в научных областях, но и в профессиональной области, и в социальной, экономической, политической сферах жизни общества. Поясним это подробнее.

1. Каждый из нас каждый день решает ряд самых разнообразных задач. Любую проблему можно рассматривать как задачу, которую необходимо решить.

2. Каждый учитель при проектировании учебно-воспитательного процесса формулирует определённые цели, которые распадаются на задачи. Это педагогические задачи.

3. Анализируя учебный материал по предмету, педагог для усвоения теории предлагает обучающимся упражнения, которые можно рассматривать как задачи особого рода. Это задачи учебного характера.

Итак, подобно атому и клетке – задача как категория является той отправной точкой, от которой стоит отталкиваться в педагогике, философии, социологии, политике и т.п. В своей магистерской диссертации мы анализируем этот вопрос.

В заключении продемонстрируем использование задачного подхода в образовательном процессе на примере географии.

Так при изучении темы « Вулканы» в 6 классе обучающимся предлагается выполнить проект или самостоятельную поисковую работу по данной теме. Содержательная модель проекта представлена на слайде.

Источник

Задачный подход к обучению. Обучение поиску решения задач

Разделы: Математика

Корабль образования должен двигаться галсами, ибо движение в одном направлении либо приведёт его в тупик, либо посадит на мель. 30 лет назад реформа математического образования, контуры которой задал А.Н.Колмогоров, приняла одно из возможных направлений. Наступило время сделать очередной галс. Речь ни в коем случае не должна идти об отказе от уже сделанного, о возврате назад, а лишь о некотором повороте, отражающем произошедшие за это время кардинальные изменения в обществе. Из чего исходить при выборе нового направления?

Всё это показывает необходимость более решительно подходить к реформе математического образования, прекратить топтаться на месте, поскольку математическое образование наиболее способствует:

Математика универсальна, всеобща, приобщает к мировой культуре именно потому не существует национальной, ведомственной или государственной математики.

Всё это заставляет задуматься о возможности осторожных и продуманных изменений как в содержании, так и в методических технологиях школьного математического образования. Одной из таких технологий является – система задач и задачный подход к обучению.

Самое главное найти у каждого ученика мотив к учению и самое трудное в работе учителя поиск необходимых инструментов прикосновения к личности. Как сформировать у учащихся интерес к предмету, научить самостоятельно и творчески добывать знания, активно участвовать в процессе обучения, уметь анализировать и оценивать свои знания – эти вопросы волновали меня как учителя. Помогла технология постановки целей (М.Е.Бершадский, В.В.Гузеев) – система задач и задачный подход к обучению.

Методы нахождения решений и психическая деятельность, связанная с поиском решения, во многом сходны как в жизненных или производственных задачах, так и в школьных (по математике, физике, химии). Поэтому ознакомление учащихся с методами поиска решений является средством не только улучшения учебных навыков, но и воспитания учащихся, подготовки их к будущей производственной деятельности, к жизни. От эффективности применения задач в обучении математике во многом зависит и степень подготовленности школьников к практической деятельности в любой сфере производства, народного хозяйства и культуры.

Решая математические задачи, представленные в продуманной системе, учащиеся не только активно овладевают содержанием курса математики, но и приобретают умения мыслить творчески. Это проявляется, например, в умении изменить условие задачи с целью применить тот или иной метод, приём в умении изобретать новые приёмы для решения задач; в умении выделять и накапливать потенциально полезную информацию; умение конструировать на базе данной задачи новые; в умении осуществлять самоконтроль, исследовать результат решения.

Поэтому можно утверждать, что педагогические основы использования задач в современном школьном обучении правомерно являются тем средством обучения, без применения которого невозможно активное и прочное усвоение учащимися программного материала, их всестороннее воспитание и развитие, приобщение к труду творческого характера.

В связи с этим уместно напомнить высказывание известного педагога- математика Д.Пойа: «Что значит владение математикой? Это есть умение решать задачи, причём не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности. Поэтому первая и самая главная обязанность курса математики средней школы состоит в подчёркивании методической стороны процесса решения задач». Этому способствует задачный подход к обучению.

По традиции в школьной практике в одних случаях осуществляется постепенный переход от метода шаблонных задач к методу нешаблонных, а в других такой постепенный переход не соблюдается. Когда не соблюдается постепенный переход от метода шаблонных задач к методу нешаблонных, нарушаются дидактические принципы последовательного преодоления трудностей, доступности, что приводит к плохим знаниям. Осуществляя постепенный переход от метода шаблонных задач к методу нешаблонных, ускоряя такой переход в случае работы с сильными классами, и, наоборот, переходя к простейшим, порой примитивнейшим упражнениям в слабых классах, отрабатывая в последних умения и навыки проведения тех преобразований, вычислений и рассуждений, которыми должны были обладать учащиеся, но, к сожалению, не обладают, мы всегда можем осуществить дидактические принципы последовательного преодоления трудностей, доступности, полноты, сравнения и т.д.

Ныне действующие программы по математике не предусматривают изучение каких-либо теоретических основ о задачах и их решении. Теоретические знания о задачах и их решении нужны учащимся для того, чтобы они могли производить решение разнообразных задач сознательно и целенаправленно, а не только лишь на основе подражания, по аналогии с ранее решёнными задачами. Конечно, такие аналогии нужны, но если ученик при встрече с незнакомой задачей ограничивается лишь поиском аналогий, то неминуемы ошибки, а в большинстве случаев решение вовсе не будет найдено. Поиск решения незнакомых задач должен вестись школьниками культурно и сознательно, с полным пониманием сущности самой задачи и её решения. Важнейшими элементами любого метода поиска решения являются анализ и синтез. При решении математических задач синтез может использоваться в двух формах рассуждения: 1) когда двигаются от данных к искомым фактам; 2) когда элементы объединяют в одно целое. Точно так же и анализ может выступать в двух формах: 1) когда в рассуждениях двигаются от искомых к данным задачи; 2) когда целое (фигуру, выражение и т.п.) расчленяют на части.

Остановимся ещё на одном моменте, который играет важную роль в процессе поиска решения. Во время раздумья над возможными путями решения задачи учащемуся пришёл в голову некоторый «шажок мысли». Правильным ли он является? Критерием в этом вопросе является прогнозирование, т. е. предвидение результата, получаемого в процессе анализа, синтеза, обобщения. Формирование умения прогнозировать, предвидеть результаты, к которым приведёт каждый отдельный шажок мысли, является важным компонентом развития мышления. С этой целью на уроках математики при обсуждении идеи решения, когда кто-либо из учащихся предлагает воспользоваться той или иной формулой, теоремой, тождественным преобразованием, целесообразно добиваться того, чтобы он обосновывал разумность своего предложения и хотя бы в общих чертах указывал, к чему оно приведёт. Тем самым перед всем классом раскрывается аналитико-синтетический ход рассуждений одного из учащихся, а остальные приучаются прогнозировать процесс поиска решения задачи.

Невозможно сказать, как возникает решение трудной задачи. Вспомним три из «десяти заповедей учителя» Д.Пойа:

6. Старайтесь научить своих учеников догадываться.
7. Старайтесь научить своих учеников доказывать.
10. Пользуйтесь наводящими указаниями, но не старайтесь навязывать своего мнения насильно.

В каждом способе решения задач какого-либо вида, в самом решении этих задач, в умениях, формируемых при этом, содержатся как чисто специфические черты, присущие лишь способу и умениям, соответствующим данному виду задачи, так и некоторые общие черты, присущие методам и умениям по решению любых математических задач. Поэтому при решении задач того или иного вида надо в первую очередь подчёркивать и выделять общие методы решения задач: разбиение на подзадачи, разбиение области задачи на части, сведение данной задачи к ранее решённым, модельные преобразования задачи.

Значит, задача учителя состоит в следующем: сформировать такой общий подход к решению задач, когда задача рассматривается как объект для анализа, для исследования, а её решение – как конструирование и изобретение способа решения. Естественно, что такой подход требует не бездумного решения огромного числа задач, а неторопливого, внимательного и обстоятельного решения значительно меньшего числа задач, но с серьёзным последующим анализом проведённого решения, выявления в нём общих методов и приёмов решения любых математических задач.

Главное при этом – разбудить дремлющие силы самого ученика, вызвать у него ненасыщаемую жажду знаний, желание самосовершенствования.

Задачный подход к обучению имеет свои закономерности, принципы, правила и требования. Они являются ориентиром в моей работе. К ним относятся: полнота, наличие ключевых задач, связность, возрастание трудности в каждом уровне, целевая ориентация, целевая достаточность, гибкость, психологическая комфортность.

1. Полнота. Наличие задач на все изучаемые понятия, факты, способы деятельности, включая мотивационные, подводящие под понятие, на аналогию, следствие из фактов.

2. Наличие ключевых задач. Группировка задач в узлы вокруг объединяющих центров – задач, в которых рассматриваются факты или способы деятельности, применяемые для решения других задач и имеющие принципиальное значение для усвоения предметного содержания.

3. Связность. Вся совокупность задач графически может быть представлена связным графом, в узлах которого – ключевые задачи, выше них – подготовительные и вспомогательные, ниже – следствия, обобщения и так далее.

4. Возрастание трудности на каждом уровне. Система задач состоит из трёх подсистем, соответствующих минимальному, общему и продвинутому уровням планируемых результатов обучения. В каждой из подсистем трудность задач непрерывно нарастает.

5. Целевая ориентация. Для каждой задачи определено её место и назначение в блоке уроков.

6. Целевая достаточность. Достаточно задач для тренажа в классе и дома, аналогичных задач для закрепления методов решения, задач для групповых и индивидуальных заданий разной направленности, задач для самостоятельной (в том числе и исследовательской) деятельности учащихся, задач для текущего итогового контроля с учётом запасных вариантов.

7. Гибкость. Гибкость задачного подхода выражается в обеспечении возможности приспособления содержания обучения и путей его усвоения к индивидуальным потребностям обучаемых. Надо обеспечить индивидуальный темп усвоения, индивидуальную технологию обучения.

8. Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти. Есть задачи для устных упражнений, письменного выполнения, чтение чертежа, задачи-шутки и другие. Каждое задание, предлагаемое учителем (там, где это возможно), должно иметь словесное, графическое, предметно-иллюстративное решение. Ученик вправе выбрать какое-либо одно и может рассчитывать на успех, что будет усиливать его учебную мотивацию. Это особенно важно в старших классах, где дидактический материал разнообразен по содержанию, форме и объёму.

Рассмотрим всё выше сказанное на примерах.

«Метод интервалов при решении неравенств»

Предлагаю решить неравенство: (а+2)(а+3)≥0.

Решением его является объединение двух промежутков (-∞;- 3) (- 2; +∞).

Далее предлагаю решить методом интервалов другие неравенства. Но так, чтобы, видоизменяя неравенство можно было увидеть, и как изменяется его решение.

а) ;

б) (.

Полезно также предложить учащимся неравенства, которые решаются по смыслу:

а)

б)

в) .

Ранее рассмотренные неравенства можно использовать для решения уравнений.

Упражнения, которые составляются и решаются по аналогии

Другими словами, мы находим общий способ решения различных по заданию задач.

Например, решаем уравнение с одной переменной (х 2 – 4х + 3) 2 + (х 2 – 1,5х + 0,5) 2 = 0.

Равенство верно, если

х 2 – 4х + 3 = 0;
х 2 – 1,5х + 0,5 = 0. Отсюда, х = 1.

Затем можно дать уравнение с двумя переменными, которые решаются аналогично первому:

Если предложить учащимся решить квадратное уравнение с двумя переменными типа

3) х 2 + у 2 + 6х – 2у + 10 = 0 после решения квадратных уравнений с одной переменной, то обычно они испытывают трудность в поиске его решения, но если им предложить это уравнение после решения уравнений 1) и 2), то ученики легко находят способ решения, рассуждая по аналогии. Действительно, для этого достаточно привести уравнение (3) к виду: (х 2 + 6х + 9) + (у 2 – 2у + 1) = 0, (х + 3) 2 + (у – 1) 2 = 0.

(х + у) 2 ≥0 и (4у 2 + х 2 + 1)>0 при всех значениях переменных. Следовательно, 2х 2 + 5у 2 + 2ху + 1 >0.

Подобный подход к осмыслению материала уроков позволяет найти не только общие методы решения задач, но и способы уплотнения урока.

Задачный подход к обучению можно использовать в каждом классе, каждым учителем. Этот подход позволяет поверить ученику в свои силы, совместная работа учителя и ученика даёт эффект сотрудничества, позволяет видеть своё продвижение по мере нарастания трудности задач. При этом способе работы возможно разноуровневое (дифференцированное) обучение: для сильных учащихся задачи продвинутого уровня, больший объём теоретического материала, работа с дополнительными учебниками, задачниками; для слабых – задачи минимального уровня, больше помощи со стороны учителя.

Здесь, мне кажется, уместным сформулировать один из принципов обучения школьников, который Хазанкин Р.Г. называет принципом «четырёх СО».

Урок математики – это:

Источник