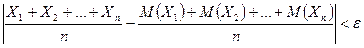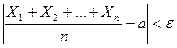значение теоремы чебышева на практике
Неравенство Маркова. Неравенство Чебышева
На этой странице мы собрали примеры решения учебных задач по теории вероятностей, в которых применяются неравенство Маркова, неравенство Чебышева, теорема Чебышева и их следствия (закон больших чисел, ЗБЧ).
Краткая теория. Закон больших чисел
Неравенство Маркова дает вероятностную оценку того, что значение неотрицательной случайной величины превзойдет некоторую константу через известное математическое ожидание. Когда никаких других данных о распределении нет, неравенство дает некоторую информацию, хотя зачастую оценка груба или тривиальна.
Альтернативная форма записи (когда нужно оценить вероятность того, что СВ меньше некоторой константы):
Когда известны не только математическое ожидание (первый момент), но и дисперсия (второй центральный момент) для случайной величины (и они конечны), можно применять следствие неравенства Маркова — неравенство Чебышева, которое дает оценку вида:
Также его можно записать в другой форме:
Приведем также теорему Чебышева, которая имеет большое практические значение.
Примеры решенных задач
Неравенство Маркова: примеры решений
Задача 1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500.
Задача 2. Количество потребляемой за сутки электроэнергии предприятием является случайной величиной с математическим ожиданием 6 мегаватт при среднем квадратическом отклонении 1,5 мегаватта. Оценить вероятность того, что в ближайшие сутки потребление электроэнергии окажется более 12 мегаватт.
Неравенство Чебышева: примеры решений
Задача 4. В 1600 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,3. С помощью неравенства Чебышева оценить вероятность того, что разница между числом успехов в этих испытаниях и средним числом успехов будет меньше 50.
Задача 6. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух.
Теорема Чебышева и ЗБЧ: примеры решений
Задача 8. Вероятность того, что абсолютная величина отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не превышает 0,5, равна 0,8. Дисперсия каждой независимой случайной величины не превышает 7. Найти число таких случайных величин.
Задача 9. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.
Решебник по терверу
Нужны еще решения? Найди в решебнике сейчас:
Значение теоремы Чебышева для практики
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.
В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
4. Теорема Бернулли.
Пусть производится 


Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846г.
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Другими словами, если 
Задача 1. Длина изготовляемых изделий представляет случайную величину, среднее значение которой (математическое ожидание) равно 90 см. Дисперсия этой величины равна 0,0225. Оценить вероятность того, что длина изделия выразится числом, заключенным между 89,7 см. и 90,3 см.
Решение: Случайная величина 






Заменим это неравенство равносильным 



Задача 3. Вероятность вызревания кукурузного стебля с тремя початками равна ¾. Оценить вероятность того, что среди 3000 стеблей, доля стеблей с тремя початками будет по абсолютной величине отличаться от вероятности вызревания такого стебля не более, чем на 0,02.
Решение: 




Воспользуемся неравенством из теоремы Бернулли:


Вероятность отклонения не менее 0,84, т.е. найдена нижняя граница вероятности.
Тема 11 «ВАРИАЦИОННЫЕ РЯДЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»
«ВАРИАЦИОННЫЕ РЯДЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»
1. Задачи математической статистики.
2. Генеральная совокупность и выборка.
3. Вариационный ряд.
4. Полигон и гистограмма.
5. Средние величины вариационного ряда.
6. Показатели вариации вариационного ряда.
7. Начальные и центральные моменты вариационного ряда.
Теорема Чебышева. Ее сущность и значение для практики
Лекция 24 Закон больших чисел и предельные теоремы теории вероятностей.
Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания. Это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, если о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим.
Теорема Чебышева. Если 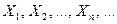
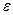
будет как угодно близка к единице, если число случайных величин достаточно велико.
Другими словами, в условиях теоремы
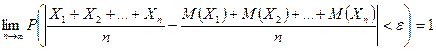
Формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. Однако на практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. И если допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.
Обозначим математическое ожидание каждой из случайных величин через 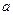
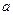
Если 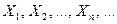
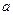
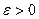
будет как угодно близка к единице, если число случайных величин достаточно велико.
Сущность теоремы Чебышева заключается в том, что хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу 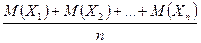
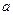
Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.
Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.
В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Теорема Чебышева как фундамент современной теории вероятностей
Погружаясь в мир случая, важно понимать, что значение случайной величины в любой момент времени возможно определить лишь с некоторой вероятностью. Казалось бы, наши знания достаточно ограничены, чтобы определить какие-либо закономерности в поведении случайных величин и давать прогнозы хотя бы в первом приближении. Именно эту проблему и решил знаменитый русский математик Пафнутий Львович Чебышев, сформулировав свою знаменитую теорему.
В чем суть теоремы Чебышева?
Для практики очень важно по небольшой выборке объектов сделать выводы о том или ином свойстве генеральной совокупности. Именно здесь в дело вступает закон больших чисел, строго говоря, состоящий из теорем Чебышева (наиболее общего) и Бернулли (частного).
Текстовая формулировка: при неограниченном увеличении числа независимых испытаний значение случайной величины сходится по вероятности к ее математическому ожиданию.
На пальцах это звучит так: хотя мы и не можем предсказать конкретное значение случайной величины, мы можем с вероятностью, близкой к единице, определить её среднее арифметическое, чего будет более чем достаточно на практике.
Важное свойство:среднее арифметическое в данному случае уже не является случайной величиной!
Конкретных примеров применения теоремы Чебышева в реальной жизни огромное количество:
1. Проведение измерений: при достаточно большом количестве измерений, например, напряжения в сети, можно получить значение, сколько угодно близкое к истинному.
2. Проверка качества. Нет необходимости, например, проверять всю партию однообразных товаров, а достаточно выборочной проверки.
3. Страхование. Рассматривая величину страхового взноса, страховщик обладает определенной информацией о вероятности наступления страховых случаев и возможных потерях клиента от них. По теореме Чебышева найдя среднее арифметическое от этих убытков, страховщик может определить идеальную величину страхового взноса: выгодную для него и привлекательную для клиента.
4. Финансовые рынки. Проведение большого числа финансовых операций с известной средней ожидаемой доходностью лежит в основе диверсификации рисков.
Значение теоремы чебышева для практики
Приведем примеры применения теоремы Чебышева к решению практических задач.
Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебышева (ее частный случай).
Действительно, рассмотрим результаты каждого измерения как случайные величины
К. этим величинам можно применить теорему Чебышева, если:
1) Они попарно независимы.
2) имеют одно и то же математическое ожидание,
3) дисперсии их равномерно ограничены.
Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных.
Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а.
Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено.
Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства
Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов.
Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.
В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
Производится п независимых испытаний (не событий, а испытаний). В каждом из них вероятность появления события A равна р.
Возникает вопрос, какова примерно будет относительная частота появлений события? На этот вопрос отвечает теорема, доказанная Бернулли[2] которая получила название закона больших чисел и положила как науке.
Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Замечание. Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство
В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет, как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.
1. Оценить вероятность того, что при 3600 бросаниях кости число появления 6 очков будет не меньше 900.