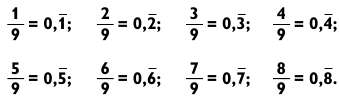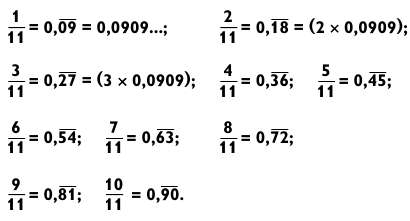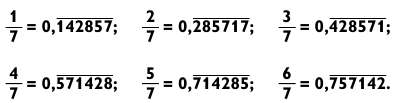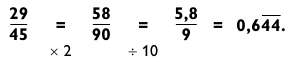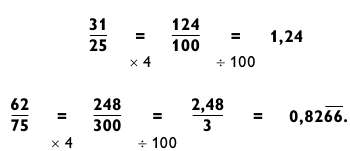как в уме разделить 60 на 4

Как быстро считать в уме: приемы устного счета больших чисел

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

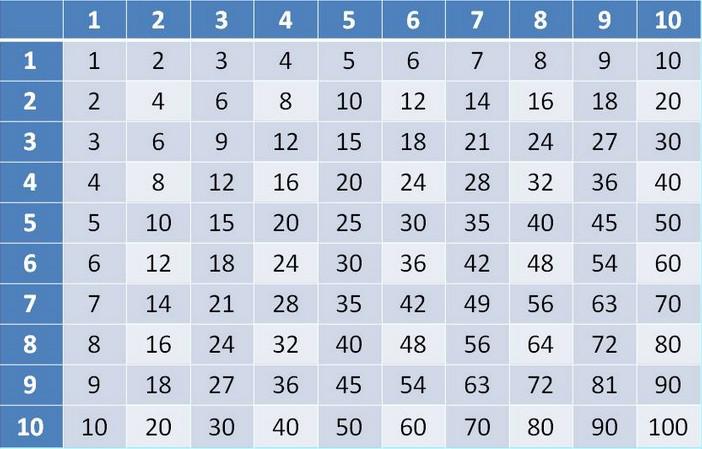
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Проверим и умножим 54 на 11.

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Как научиться быстро считать в уме?

Всего несколько месяцев ежедневных тренировок по 5-10 минут, и вы почувствуете, как ускорился ваш мозг.

Сложение

Начнём с простого — сложения однозначных чисел. Научившись мгновенно складывать однозначные числа, вы сможете легко складывать и многозначные числа, потому что все расчёты сводятся к выполнению типовых действий. Вы в этом скоро убедитесь.

Сложение однозначных чисел

С примерами, результаты которых находятся в пределах 10 проблем нет. Эти комбинации чисел нужно просто запомнить, как основу основ.

А вот для примеров «с переходом через 10» уже есть методика — «опора на десяток». Суть в том, чтобы довести одно слагаемое до 10, а потом из второго слагаемого вычесть столько же, сколько мы прибавили к первому.

Например, нам нужно сложить 5 и 8:

Сложение многозначных чисел

Принцип сложения многозначных чисел — складывать друг с другом одинаковые разряды: тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами.

Например, нам нужно сложить 245 и 917:

Вычитание

Как и со сложением, с вычитанием однозначных чисел из однозначных ничего сложного нет. А при вычитании однозначного числа из двузначного удобно пользоваться тем же правилом «опоры на десяток».

Вычитание однозначных числа

Например, нужно вычесть 13 − 7:

Вычитание многозначных чисел

Здесь всё даже проще, чем со сложением многозначных чисел, потому что на разрядные части нужно разложить только то число, которое вычитаем.

Например, нужно вычесть 734 − 427:

Убираем 4 из 314 и 7, получаем 310 − 3. Ну а тут уже совсем просто — ответ 307.

Чтобы вычитать 7, 8 и 9 было проще, часто прибегают к следующим правилам:

321 − 7 = 321 − 10 + 3 = 314

Умножение

Это когда несколько раз складывают одно и то же. Например, 7 × 3 = 7 + 7 + 7 = 21.

Чтобы научиться быстро умножать любые числа в уме (кроме совсем уж космических), нужно идеально умножать однозначные числа, то есть знать таблицу умножения.

Причём идеально знать её необязательно, достаточно запомнить для себя опорные числа, которые будут помогать в вычислениях. Умножим 6 × 7. Мнемотехнически мы знаем что 6 × 6 = 36. То есть к 36 нужно прибавить ещё 6, чтобы получился ответ — 42.

Считается, что из всех примеров в таблице умножения 7 × 8 самый сложный. Чтобы запомнить ответ есть отличное правило «пять шесть семь восемь»: 56 = 7 × 8.

Умножение однозначного числа на двузначное

3 × 8 × 100 = 24 × 100 = 2400.

2400 + 640 + 56 = 2000 + 400 + 600 + 40 + 50 + 6 = 2000 + (400 + 600) + (40 + 50) + 6 = 2000 + 1000 + 90 + 6 = 3000 + 90 + 6 = 3096

Например, 237 × 2. Сначала проще умножить 240 × 2 = 480. А потом вычесть из результата 6 (3 × 2 = 6 — ведь 3 нам не хватало до 240). Итого:

Правда, если сумма двух цифр исходного числа больше 10, нужно поставить разряд единиц между цифрами исходного числа, а десяток прибавить к левой цифре:

Умножение двузначных чисел

Хотя кажется, что умножать двузначные числа — вершина ментальных вычислений, решать такие примеры не сильно сложнее, чем в предыдущем пункте. Давайте разберём на примере.

2490 + 332 = 2000 + 400 + 300 + 90 + 30 + 2 = 2000 + 700 + 120 + 2 = 2822.

Деление

Это операция, обратная умножению. Начнём снова с самого простого.

Деление двузначного числа на однозначное

Разделим 48 : 3. Основная задача — подобрать число, которое можно умножить на 3 и получить 48. Из таблицы умножения мы помним, что единственное число, результат умножения которого на 3 в конце имеет цифру 8 — это 6. А 3 × 6 = 18. То есть, у нас остаётся 30 : 3 = 10. Итого, получается 48 : 3 = 16.

Деление многозначного числа на однозначное

Разделим 6475 : 7. В подобных примерах главная задача — «взять» максимальные «круглые» части, которые можно разделить на 6 без остатка.

Деление на двузначное число

С делением на двузначное число всё гораздо интереснее. Задача в том, чтобы найти пределы, в которых лежит результат.

Например, разделим 6351 : 73:

12 × 25 = 12 : 4 × 100 = 3 × 100 = 300

Этих способов достаточно, чтобы тренироваться уверенно считать в уме. Помните, что делать это нужно регулярно, уделяя всего по 5–10 минут каждый день. Постарайтесь поймать свой ритм, чтобы решение таких задачек приносило удовольствие. И упирайте на правильность ответов, а не скорость — она придёт со временем. И не бросайте.

А если вам нужна помощь в решении более сложных задач, которые уже нельзя просчитать в уме, вам с радостью помогут специалисты Мультиворка.

Источник

Глава 4 Разделяй и властвуй: деление в уме

Разделяй и властвуй: деление в уме

Деление в уме — чрезвычайно полезный навык как для бизнеса, так и для повседневной жизни. Сколько раз в неделю вы сталкиваетесь с ситуациями, которые требуют от вас что-то равномерно распределить, например счет в ресторане? Точно такой же навык оказывается кстати, когда вы хотите выяснить стоимость одной упаковки корма для собак, или поделить выигрыш во время игры в покер, или узнать, сколько литров бензина можно купить на 20 долларов. Способность делить в уме избавит вас от необходимости постоянно обращаться к калькулятору, когда вам нужно что-либо посчитать.

При выполнении устного деления метод вычисления слева направо вступает в свои права. Именно ему нас учили в школе, так что вы будете заниматься естественным для себя делом. Помню, что, будучи ребенком, думал, будто метод деления слева направо олицетворяет то, какой арифметика должна быть в принципе. Я часто размышлял о том, что если бы в школе нашли способ преподавать и деление справа налево, они, вероятно, так бы и сделали!

ДЕЛЕНИЕ НА ОДНОЗНАЧНОЕ ЧИСЛО

Чтобы разделить 179 на 7, нужно найти такое число Q, которое 7 раз по Q составит 179. Очевидно, что поскольку 179 находится между 7 х 10 = 70 и 7 х 100 = 700, Q должно размещаться между 10 и 100. Стало быть, ответ является двузначным числом. Зная это, сначала определяем наибольшее кратное 10, которое может быть умножено на 7 и в итоге оказаться меньше 179. Нам известно, что 7 х 20 = 140 и 7 х 30 = 210, значит, ответ будет в диапазоне «20 плюс». Отталкиваясь от этого, мы уже можем реально проговорить число «20», так как это будет часть ответа, и она точно не изменится. Далее вычитаем 179–140 = 39. Теперь наша задача сведена к делению 39 х 7. Так как 7 х 5 = 35, что на 4 меньше 39, у нас появилась вторая часть ответа «5» с остатком 4, или, если вы предпочитаете говорить так: 25 и 4/7. Вот как выглядит данный процесс деления[3].

Попробуем решить похожую задачу, используя аналогичные расчеты.

Схематически данный пример представим так:

Теперь рассмотрим пример, при решении которого получается трехзначное число.

На этот раз ответ будет содержать три цифры, потому что 947 находится между 4 х 100 = 400 и 4 х 1000 = 4000. Нам следует отыскать наибольшее кратное 100, наиболее близкое к 947.

В совокупности имеем 236 с остатком 3, или 236 и 3/4.

Процесс деления четырехзначного числа на одну цифру столь же прост, как и следующий пример.

Здесь ответ будет исчисляться сотнями, потому что 2196 находится между 5 х 100 = 500 и 5 х 1000 = 5000. После вычитания 5 х 400 = 2000 из 2196 мы можем произнести «400», и наша задача сведется к деления 196 на 5, что вычисляется так же, как и в предыдущих примерах.

УПРАЖНЕНИЕ: ДЕЛЕНИЕ НА ОДНУ ЦИФРУ

ПРАВИЛО БОЛЬШОГО ПАЛЬЦА

При делении в уме запоминание частей ответа может вызвать сложности в процессе вычислений. Одним из вариантов выхода из ситуации является, как мы практиковали ранее, проговаривание ответа вслух по ходу решения. Но для создания большего эффекта вы можете предпочесть (как и я) держать ответ в памяти с помощью пальцев и произносить его целиком в самом конце. Однако при этом вы рискуете столкнуться с проблемой при запоминании чисел, которые больше пяти, ведь у нас лишь пять пальцев на каждой руке. В этом вам поможет специальная техника, в основе которой лежит язык жестов. Я называю ее «Правило большого пальца». Она особенно эффективна для запоминания чисел, состоящих из трех и более цифр, и полезна не только в данной главе, но пригодится и в последующих, где придется иметь дело с задачами посложнее и числами подлиннее.

Вы уже догадались, что для запоминания чисел от 0 до 5 вам достаточно согнуть нужное количество пальцев на руке. Когда в процесс вовлечен большой палец, будет легко запомнить числа от 6 до 9. Вот список правил большого пальца.

• Чтобы задать 6, поместите большой палец на верхней части мизинца.

• Чтобы задать 7, поместите большой палец на верхней части безымянного пальца.

• Чтобы задать 8, поместите большой палец на верхней части среднего пальца.

• Чтобы задать 9, поместите большой палец на верхней части указательного пальца.

При работе с трехзначным числом задайте цифры для сотен на левой руке и для десятков на правой. Когда дело дойдет до одной цифры, вы достигнете конечной точки решения (за исключением возможного остатка). Теперь произнесите число на левой руке, число на правой руке, последнюю цифру, которую только что посчитали, и остаток (что у вас в голове).

И вот! Вы произнесли ответ!

Чтобы попрактиковаться, попробуйте решить следующую задачу на деление четырехзначного числа.

Пользуясь приемом большого пальца для запоминания ответа, вы зададите 7 на левой руке, соединив большой палец с безымянным, и 6 на правой, соединив большой палец с мизинцем. Как только вычислите последнюю цифру (она равна 3) и остаток (равный 1), можете «зачитать» итоговый ответ с ваших рук слева направо: «семь…шесть…три с остатком один».

Некоторые задачи на деление четырехзначных чисел дают четырехзначный ответ. В таком случае, поскольку у вас только две руки, вам придется вслух произнести цифру для тысячи и использовать правило большого пальца для запоминания остального ответа. Например:

Для решения этой задачи вы делите 8 на 3, чтобы получить цифру 2 для тысяч; произносите «две тысячи» вслух, затем делите 2352 на 3 привычным способом.

ДЕЛЕНИЕ НА ДВУЗНАЧНЫЕ ЧИСЛА

В этом разделе мы исходим из предположения, что вы уже освоили искусство деления на однозначные числа. Естественно, задачи на деление с увеличением делителя более сложные.

К счастью, в моем рукаве есть немного магии, чтобы облегчить вам жизнь.

Начнем с относительно простой задачи.

Так как 597 находится между 14 х 10 и 14 х 100, ответ (так называемое частное) лежит между 10 и 100. Чтобы его найти, нужно в первую очередь задать вопрос: «Сколько раз по 14 даст в сумме 590?» Умножив 14 х 40 = 560, вы узнаете, что ответ будет в диапазоне «40 плюс»; так что можно смело произнести вслух «сорок».

Далее вычитаем 560 из 597 и получаем 37, что сводит задачу к делению 37 на 14. Так как 14 х 2 = 28, здесь ответ — 42. Вычитая 28 из 37, мы получаем остаток 9. Процесс решения задачи показан следующим образом.

Следующая задачка немного сложнее, потому что делитель в ней больше.

В данном примере ответ будет двузначным числом, так как 682 находится между 23 х 10 = 230 и 23 х 100 = 2300. Чтобы найти цифру для десятка двузначного числа, нужно подумать: «Сколько раз по 23 даст в сумме 680?» Если вы попробуете 30, то увидите, что здесь незначительный перебор, так как 23 х 30 = 690. Но теперь вы знаете, что ответ лежит в диапазоне «20 плюс» и можете произнести это вслух. Затем вычтите 23 х 20 = 460 из 682, чтобы получить 222. Так как 23 х 9 = 207, ответ — 29 и остаток 222–207 = 15.

491 / 62

Так как 491 меньше, чем 62 х 10 = 620, ответ будет представлен одной цифрой с остатком. Можно попробовать 8, но 62 х 8 = 496, а это несколько больше делимого. Поскольку 62 х 7 = 434, ответ — 7 и остаток 491–434 = 57, или 7 и 57/62.

Один отличный трюк может облегчить решение таких задач. Помните, как сначала мы пытались перемножить 62 х 8 = 496, но обнаружили, что это число больше, чем нужно? Но это действие оказалось не напрасным. Помимо информации о том, что ответ — 7, оно также позволяет сразу определить остаток.

Поскольку 496 на 5 единиц больше 491, остаток будет на 5 единиц меньше делителя 62. Поскольку 62 — 5 = 57, то ответ — 7 и 57/62. Этот прием работает потому, что 491 = (62 х 8) — 5 = 62 х (7 + 1) — 5 = (62 х 7 + 62) — 5 = (62 х 7) + (62 — 5) = 62 х 7 + 57.

Следующий вызов для вас — деление четырехзначного числа на двузначное.

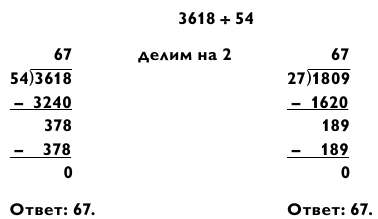
3657 / 54

Так как 54 х 100 = 5400, то ответ будет двузначным числом. Для получения первой цифры ответа необходимо выяснить, сколько раз по 54 даст в сумме 3657. Исходя из того что 54 х 70 = 3789 (что немного больше делимого), ответ будет где-то в диапазоне «60 плюс».

Теперь попробуйте свои силы в решении задачи с трехзначным частным:

Упрощение задач на деление

Как видите, остатки 10 и 5 различны; но если записать их в виде дроби, получится 10/16, что равно 5/8. Поэтому в данном методе ответ всегда должен быть представлен в виде дроби.

Мы проделали оба типа вычислений для того, чтобы вы убедились, насколько второй способ легче. Теперь ваша очередь практиковаться:

Мне кажется, что проще дважды разделить числа на 2, чем делить каждое из чисел на 4. Теперь рассмотрим случай, когда оба числа оканчиваются на 0. В этой ситуации можно каждое число разделить на 10.

Если оба числа заканчиваются на 5, удвойте их, а затем разделите на 10 для упрощения задачи. Например:

Наконец, если делитель оканчивается на 5, а делимое на 0, умножьте оба на 2, а затем разделите на 10 и далее действуйте так, как мы делали выше.

УПРАЖНЕНИЕ: ДЕЛЕНИЕ НА ДВУЗНАЧНЫЕ ЧИСЛА

Здесь вы найдете разнообразные задачи по делению на двузначные числа, которые проверят ваше ментальное мастерство и умение пользоваться простыми техниками упрощения, которые были объяснены в этой главе. Загляните в конец книги для получения объяснений и сверки ответов.

РАЗВИВАЕМ СВОИ СПОСОБНОСТИ: ИЗУЧЕНИЕ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ

Как вы уже, наверное, догадались, мне нравится заниматься магией, превращая обычные дроби в десятичные. В случае с дробями, в знаменателе которых есть только одна цифра, лучший способ превратить их в десятичные — это почерпнуть их значения из памяти. Это не так сложно, как кажется. Далее вы увидите, что большинство дробей, числители и знаменатели которых представлены однозначными числами (а также 10 или 11), обладают особыми свойствами, поэтому их сложно забыть. Каждый раз, когда вы можете сократить дробь до уже известного вам значения, это ускорит процесс вычислений.

Уверен, вы уже знаете десятичные эквиваленты для следующих дробей:

1/2 = 0,50;

1/3 = 0,333…;

2/3 = 0,666…

1/4 = 0,25;

2/4 = 1/2 = 0,50;

3/3 = 0,75.

Дроби с пятерками в знаменателе запомнить легче всего.

1/5 = 0,20;

2/5 = 0,40;

3/5 = 0,60;

4/5 = 0,80.

Дроби с шестерками в знаменателе требуют запоминания только двух новых значений.

1/6 = 0,1666…;

2/6 =1/3 = 0,333…;

3/6 = 1/2 = 0,50;

4/6 = 2/3 = 0,666…;

5/6 = 0,8333…

Через мгновение я вернусь к дробям с семерками в знаменателе. А сейчас дроби с восьмерками в знаменателе, преобразовать которые просто элементарно.

1/8 = 0,125;

2/8 = 1/4 = 0,25;

4/8 = 1/2 = 0,50;

6/8 = 3/4 = 0,75;

Дроби с девятками в знаменателе таят в себе особое волшебство.

где черта над цифрой обозначает бесконечное повторение этой цифры (говорят, что это дробь в периоде). Например, 4/9 = 0,444…

Дроби с десятками в знаменателе нам уже известны.

1/10 = 0,1; 2/10 = 0,2; 3/10 = 0,3;

4/10 = 0,4; 5/10 = 0,5; 6/10 = 0,6;

7/10 = 0,7; 8/10 = 0,8; 9/10 = 0,9.

Дроби со знаменателем 11 легко вычисляются, если вы запомните, что 1/11 = 0,0909.

Дроби со знаменателем 7 действительно выдающиеся. Как только вы запомните, что 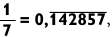то сможете без труда получить значения других дробей с 7 в знаменателе.

Обратите внимание, что последовательность цифр в периоде циклически повторяется в каждой дроби, при этом изменяется лишь начальная цифра последовательности. Ее можно определить путем умножения 0,14 на числитель дроби.

Например, для дроби 2/7 имеем 2 х 0,14 = 0,28. Поэтому последовательность должна начинаться с 2. Для дроби 3/7 это 3 х 0,14 = 0,42, значит, последовательность начинается с 4.

Другие дроби подчиняются тому же правилу.

Конечно, в процессе решения разнообразных задач вы обязательно столкнетесь с дробями, превышающими 10/11. Поэтому постоянно обдумывайте способы упрощения таких задач. Например, можно упростить дробь 18/34 путем деления числителя и знаменателя на 2, чтобы сократить задачу до 9/17 (ее будет легче решить).

Если знаменатель дроби — четное число, можно упростить дробь, уменьшив ее вдвое, даже если числитель нечетный.

9/14 = 4,5/7

Деление числителя и знаменателя на 2 сведет проблему к дроби с семеркой в знаменателе. Хотя ранее показанная последовательность дробей не предоставляет десятичного варианта для дроби 4,5/7, как только вы начнете считать, заученное число неожиданно всплывет в памяти.

Как видите, вам не пришлось решать задачу целиком.

Стоит вам разделить 3 на 7, и вы точно произведете огромное впечатление на публику, отбарабанив этот длинный набор цифр почти мгновенно![4]

Когда делитель заканчивается на 5, то почти всегда умножение на 2, а потом деление на 10 оправдывает себя. Например:

Числа, которые заканчиваются на 25 или 75, надо сначала умножить на 4 и затем разделить на 100.

Этот трюк можно применять даже в середине расчетов.

Если вам нужно вычислить дробь 3/16, произойдет вот что:

Как только задача сведется к вычислению 14/16, можно привести ее к виду 7/8, что, как известно, равняется 0,875.

Отсюда 3/16 = 0,1875[5].

УПРАЖНЕНИЕ: ПРИВЕДЕНИЕ ДРОБЕЙ К ДЕСЯТИЧНОЙ ФОРМЕ

Чтобы решить следующие задачи, не забудьте использовать полученные знания о десятичном виде различных «одноцифровых» дробей. Везде, где это целесообразно, упрощайте дроби, прежде чем преобразовать их в десятичные.

1. 2/5 2. 4/7 3. 3/8 4. 9/12 5. 5/12 6. 6/11

7. 14/24 8. 13/27 9. 18/48 10. 10/14 11. 6/32 12. 19/45

В последнем разделе мы узнали, как упростить задачи на деление, если числитель и знаменатель поделить на общий множитель. В завершение этой главы обсудим, как определить, является ли одно число делителем другого. Это поможет упростить задачу на деление и ускорить процесс решения многих задач на умножение, а также пригодится, когда мы доберемся до продвинутого умножения, где часто придется искать способы разложить на множители двух-, трех- или даже пятизначные числа. Умение делать это окажется весьма полезным.

Проверить, делится ли число на 2, довольно просто. Вам нужно только определить, является ли последняя цифра четной. Если это 2, 4, 6, 8 или 0, то число целиком делится на 2.

Чтобы протестировать число на делимость на 4, проверьте, делятся ли на 4 две его последние цифры. Число 57 852 кратно 4, потому что 52 = 13 х 4. Число 69 346 не кратно 4, поскольку 46 не делится на 4 без остатка. Это правило работает потому, что 4 делит 100 и, следовательно, любое число, кратное 100.

Таким образом, поскольку 57 800 и 52 делятся на 4, то 4 поделит и их сумму, то есть 57 852.

Когда дело доходит до делимости на 3, предлагаю запомнить одно простое правило: число делится на 3 тогда и только тогда, когда сумма составляющих его цифр делится на 3 (независимо от того, сколько цифр в числе). Чтобы выяснить, делится ли 57 852 на 3, просто сложите 5 + 7 + 8 + 5 + 2 = 27. Так как 27 кратно 3, то и 57 852 будет кратно 3. Столь же удивительное правило справедливо и для делимости на 9. Число делится на 9 тогда и только тогда, когда сумма составляющих его цифр кратна 9. Поэтому 57 852 кратно 9, тогда как число 31 416, сумма цифр которого равна 15, на 9 не делится. Объясняется это правило тем, что числа 1, 10, 100, 1000, 10000 и т. д. всегда на единицу больше кратного 9.

Число делится на 6 только в том случае, если оно четное и делится на 3. Так что кратность 6 легко проверить.

Установить, делится ли число на 5, еще проще. Любое число, независимо от величины, кратно 5 тогда и только тогда, когда оно заканчивается на 5 или 0.

Выяснить делимость на 11 почти так же просто, как на 3 или на 9. Число делится на 11 тогда и только тогда, когда в результате попеременного вычитания и сложения составляющих его цифр вы получите либо 0, либо кратное 11.

Например, 73 958 не делится на 11, потому что 7–3 + 9–5 + 8 = 16. Однако числа 8 492 и 73 194 кратны 11, так как 8–4 + 9–2 = 11 и 7–3 + 1–9 + 4 = 0. Это правило работает потому, что числа 1, 100, 10 000, 1 000 000 на единицу больше кратного 11, в то время как числа 10, 1000, 100 000 и т. д. на единицу меньше величины, кратной 11.

Проверка делимости на 7 несколько сложнее. Если вы прибавите (или вычтите) число, кратное 7, к проверяемому (или из проверяемого) и полученный результат будет делиться на 7, ответ положительный. Я всегда выбираю такое прибавляемое или вычитаемое кратное 7, чтобы в итоге сумма или разность заканчивалась на 0. Например, для проверки числа 5292 я вычитаю 42 (кратное 7), чтобы получить 5250.

Далее избавляюсь от 0 на конце (так как деление на десять не влияет на проверку делимости на семь), получая в итоге 525. Затем повторяю процесс, прибавляя 35 (кратное 7), что дает мне 560. Когда я удалю 0, то останусь с числом 56, которое, как мне известно, кратно 7. Таким образом, исходное число 5292 делится на 7.

Этот метод работает не только для 7, но и для любого нечетного числа, кроме оканчивающегося на 5. Например, чтобы проверить, делится ли 8792 на 13, вычитаем 4 х 13 = 52 из 8792 и получаем 8740. Опуская 0, имеем 874. Затем прибавляем 2 х 13 = 26, выходит 900. Удаление двух нулей оставляет нас с числом 9, которое, очевидно, не кратно 13. Таким образом, 8792 не делится на 13.

УПРАЖНЕНИЕ: ПРОВЕРКА НА ДЕЛИМОСТЬ

В этом упражнении будьте особенно внимательны при проверке делимости на 7 и 17. Остальное не должно представлять для вас трудностей.

Делимость на 2

1. 53 428 2. 293 3. 7241 4. 9846

Делимость на 4

5. 3932 6. 67 348 7. 358 8. 57 929

Делимость на 8

9. 59 366 10. 73 488 11. 248 12. 6111

Делимость на 3

13. 83 671 14. 94 737 15. 7359 16. 3 267 486

Делимость на 6

17. 5334 18. 67 386 19. 248 20. 5991

Делимость на 9

21. 1234 22. 8469 23. 4 425 575 24. 314 159 265

Делимость на 5

25. 47 830 26. 43 762 27. 56 785 28. 37 210

Делимость на 11

29. 53 867 30. 4969 31. 3828 32. 941 369

Делимость на 7

33. 5784 34. 7336 35. 875 36. 1183

Делимость на 17

37. 694 38. 629 39. 8273 40. 13 855

Если вы в состоянии управиться с целыми числами, то арифметические действия с дробями покажутся вам почти такими же легкими. В этом разделе мы сделаем обзор основных методов сложения, вычитания, умножения, деления и сокращения обыкновенных дробей. Те, кто знаком с дробями, могут спокойно его пропустить.

Умножение обыкновенных дробей

Чтобы перемножить две обыкновенные дроби, нужно просто перемножить их числители (верхние числа), а затем знаменатели (нижние числа). Например:

2/3 х 4/5 = 8/15

1/2 х 5/9 = 5/18

Что может быть проще! Попробуйте следующие упражнения, прежде чем двигаться дальше.

УПРАЖНЕНИЕ: УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ

1. 3/5 х 2/7

2. 4/9 х 11/7

3. 6/7 х 3/4

4. 9/10 х 7/8

Деление обыкновенных дробей

Деление дробей столь же легкое, как и умножение. Однако оно требует одного дополнительного действия. Сначала переверните вторую дробь с ног на голову (это называется обратная дробь), а затем умножайте. Например, обратная дробь для 4/5 будет 5/4. Следовательно,

УПРАЖНЕНИЕ: ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ

Теперь ваша очередь. Поделите эти дроби.

Сокращение обыкновенных дробей

Например, 3/5 = 3/5 х 1. Но если заменить 1 дробью 2/2, то получим 3/5 = 3/5 х 1 = 3/5 х 2/2 = 6/10. Следовательно, 3/5 = 6/10.

По такому же принципу, заменив 1 дробью 3/3, получим 3/5 = 3/5 х 3/3 = 9/15. Другими словами, если мы умножаем числитель и знаменатель на одно и то же число, то получаем дробь, равную исходной.

2/3 = 2/3 х 5/5 = 10/15

Верно и то, что, деля числитель и знаменатель на одинаковое число, мы получаем дробь, равную исходной.

Это сокращение дроби.

УПРАЖНЕНИЕ: СОКРАЩЕНИЕ ДРОБЕЙ

Найдите дробь со знаменателем 12, равную дробям, представленным ниже.

1. 1/3 2. 5/6 3. 3/4 4. 5/2

5. 8/10 6. 6/15 7. 24/36 8. 20/36

Сложение дробей

Это действие можно считать простым, когда знаменатели равны. В этом случае складываются числители и сохраняется прежний знаменатель.

3/5 + 1/5 = 4/5; 4/7 + 2/7 = 6/7

Иногда можно упростить ответ. Например:

1/8 + 5/8 = 6/8 = 3/4

УПРАЖНЕНИЕ: СЛОЖЕНИЕ ДРОБЕЙ (С РАВНЫМИ ЗНАМЕНАТЕЛЯМИ)

1. 2/9 + 5/9

2. 5/12 + 4/12

3. 5/18 + 6/18

4. 3/10 + 3/10

Более коварный случай — различные знаменатели. Когда знаменатели не равны, нужно заменить исходные дроби дробями с равными знаменателями.

1/3 + 2/15

1/3 = 5/15

1/3 + 2/15 = 5/15 + 2/15 = 7/15

1/2 + 7/8

1/2 = 4/8

1/2 + 7/8 = 4/8 + 7/8 =11/8

1/3 + 2/5

1/3 = 5/15 и 2/5 = 6/15

1/3 + 2/5 = 5/15 + 6/15 = 11/15

УПРАЖНЕНИЕ: СЛОЖЕНИЕ ДРОБЕЙ (С НЕРАВНЫМИ ЗНАМЕНАТЕЛЯМИ)

1. 1/5 + 1/10 2. 1/6 + 5/18 3. 1/3 + 1/5

4. 2/7 + 5/21 5. 2/3 + 3/4 6. 3/7 + 3/5 7. 2/11 + 5/9

Вычитание дробей

Вычитание дробей похоже на их сложение. Мы покажем это действие на примерах и обеспечим вас тренировочными упражнениями.

2/5 — 2/5 = 1/5; 4/7 — 2/7 = 2/7; 5/8 — 1/8 = 4/8 = 1/2

1/3 /2/15 = 5/15 — 2/15 = 3/15 = 1/5

7/8 — 1/2 = 7/8 — 4/8 = 3/8

2/3 — 5/8 = 16/24 — 15/24 = 1/24

УПРАЖНЕНИЕ: ВЫЧИТАНИЕ ДРОБЕЙ

1. 8/11 — 3/11 2. 12/7 — 8/7 3. 13/18 — 5/18

4. 4/5 — 1/15 5. 9/10 — 3/5 6. 3/4 — 2/3

7. 7/8 — 1/16 8. 4/7 — 2/5 9. 8/9 — 1/2

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

56. Деление запятой

56. Деление запятой Вы видите здесь широкую «запятую» (рис. 51) — Она построена очень просто: на прямой АВ описан полукруг, а затем на каждой половине АВ описаны полукруги — один вправо, другой влево.Задача состоит в том, чтобы разрезать запятую одной кривой линией на две

Глава 7 Запоминающаяся глава для запоминания чисел[9]

Глава 7 Запоминающаяся глава для запоминания чисел[9] Наиболее часто мне задают вопрос о моей памяти. Нет, сразу скажу я вам, она у меня не феноменальная. Скорее, я применяю систему мнемотехники, которая может быть изучена любым человеком и описана на следующих страницах.

Глава 1

Глава 1 Кто Джон? Для того чтобы узнать, кого из двух братьев-близнецов зовут Джон, нужно спросить одного из них: «Джон говорит правду?». Если в ответ на этот вопрос последует «да», то независимо от того, лжет ли спрошенный близнец или говорит всегда только правду, он должен

Глава 2

Глава 2 1. История первая. По существу, Болванщик заявил, что варенье украли либо Мартовский Заяц, либо Соня. Если Болванщик солгал, то ни Мартовский Заяц, ни Соня не украли варенье. Но тогда Мартовский Заяц, поскольку он не украл варенье, дал правдивые показания.

Глава 3

Глава 3 14. Гусеница и Ящерка Билль. Гусеница считает, что и она, и Ящерка Билль не в своем уме. Если бы Гусеница была в здравом уме, то мнение о том, что и она, и Ящерка Билль не в своем уме, было бы ложно. Следовательно, Гусеница (будучи в здравом уме) не могла бы придерживаться

Глава 4

Глава 4 26. Сколько кренделей у каждого? Назовем одной порцией все крендельки, которые достались Соне, сколько бы их ни было. Тогда Соне досталась 1 порция. Мартовскому Зайцу досталось вдвое больше крендельков, чем Соне (потому что Соню Болванщик посадил на такое место, где

Глава 5

Глава 5 42. Появление первого шпиона. С заведомо не может быть рыцарем, так как ни один рыцарь не стал бы лгать и утверждать, будто он шпион. Следовательно, С либо лжец, либо шпион. Предположим, что С шпион. Тогда показание А ложно, значит, А шпион (А не может быть шпионом, так

Глава 6

Глава 6 52. Первый вопрос. Алиса ошиблась, записав одиннадцать тысяч одиннадцать сотен и одиннадцать как 11111, что неверно! Число 11111 – это одиннадцать тысяч одна сотня и одиннадцать! Для того чтобы понять, как правильно записать делимое, сложим одиннадцать тысяч,

Глава 7

Глава 7 64. Первый раунд (Красное н черное). Если внезапно заговоривший братец сказал правду, то его звали бы Траляля и в кармане у него была бы черная карта. Но тот, у кого в кармане карта черной масти, не может говорить правду. Следовательно, он лжет. Значит, в кармане у него

53. И снова вопрос на деление

53. И снова вопрос на деление — Давайте испытаем ее еще одной задачкой на деление, — сказала Черная Королева. — Чему равен миллион, поделенный на четверть?— Ну, это просто, четверть миллиона, конечно! — быстро ответила Алиса, — другими словами, двести пятьдесят

Глава 4

Глава 4 26. Сколько пирожков?Сколько бы пирожков ни оказалось у Сони, назовем это количество одна порция. Итак, у Сони одна порция пирожков. У Мартовского Зайца вдвое больше пирожков, чем у Сони (в условиях задачи говорится, что Соня получила лишь половину того, что досталось

Глава 7

Глава 7 graphics54 64. Первый раундЕсли бы братец говорил правду, его звали бы Траляля и у него была бы карта черной масти. Но он не может говорить правду, если у него в кармане карта черной масти. Поэтому он лжет. Это означает, что у него действительно карта черной масти, а

49. Умножение и деление

49. Умножение и деление Какие два целых числа, если разделить большее из них на меньшее, дают столько же, сколько получается при их перемножении?Подумайте, есть ли другие

49. Умножение и деление

Источник