кодирование и обработка числовой информации

Кодирование числовой информации

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.

Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.

В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:

XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.

Источник

Кодирование и обработка числовой информации

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

«IQ и EQ как основа успешного обучения»

Контрольная работа по информатике (8 класс)
по теме «Кодирование и обработка числовой информации»

1. Укажите самое большое число:

2. Как представлено число 83₁₀ в двоичной системе счисления?

3. Сколько ячеек содержит диапазон D4:E5 в электронной таблице:

8. В приведенной таблице нужно подсчитать Стоимость и Итог и построить диаграмму по наименованию и количеству проданного товара.

Стоимость = Цена * Количество

Контрольная работа по информатике (8 класс)
по теме «Кодирование и обработка числовой информации»

1) Укажите самое большое число:

2) Как представлено число 82₁₀ в двоичной системе счисления?

1) 1010010₂ 2) 1010011 ₂ 3) 100101 ₂ 4) 1000100 ₂

3) Сколько ячеек электронной таблицы в диапазоне С2: D 4?

4) Преобразуйте следующие двоичные числа в восьмеричные:

5) Преобразуйте следующие десятичные числа в двоичные:

6) Преобразуйте следующие десятичные числа в восьмеричные:

7) Преобразуйте следующие десятичные числа в шестнадцатеричные:

8. В приведенной таблице нужно подсчитать Стоимость и Итог и построить диаграмму по наименованию и количеству проданного товара.

Стоимость = Цена * Количество

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Применение облачных сервисов в педагогической практике учителя (практический курс)

Курс профессиональной переподготовки

Информатика: теория и методика преподавания в образовательной организации

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Учебное пособие на тему «Беспроводные сети»

Урок «Файлы и файловые структуры»

Рабочая программа учебного модуля «Обработка числовой информации»

ДОПОЛНИТЕЛЬНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ОБЩЕРАЗВИВАЮЩАЯ ПРОГРАММА «Flash-анимация»

Презентация по информатике на тему «Информационные системы и базы данных»

Проверочная контрольная работа 8 класс

Презентация по теме «Электронная коммерция»

Путеводитель по теме «Алгоритмы»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5131736 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Половина российских студентов отдают предпочтение гибридному формату обучения

Время чтения: 1 минута

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

ЕГЭ в 2022 году может пройти в допандемийном формате

Время чтения: 1 минута

Минобрнауки предлагает дифференцированный подход к аккредитации вузов

Время чтения: 1 минута

Роспотребнадзор опубликовал рекомендации по работе с гаджетами для школьников

Время чтения: 3 минуты

В московских школах, где будут участки для выборов, организуют выездные занятия в музеях

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

КОДИРОВАНИЕ И ОБРАБОТКА ЧИСЛОВОЙ ИНФОРМАЦИИ

КОДИРОВАНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ

Представление числовой информации с помощью систем счисления

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов

некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.

Рис. 5.1. Единичная система счисления

Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме.

В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 используются первые буквы соответствующих латинских слов (Centum — сто, Demimille — половина тысячи, МШе — тысяча).

Рис. 5.2. Римская система счисления

В римской системе счисления значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

Чтобы записать число в римской системе счисления необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:

(два десятка, пяток, три единицы).

При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Например, число 99 имеет следующее представление в римской системе счисления:

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим, причем значения цифр соседних разрядов числа различаются на величину основания.

Числа в позиционных системах счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.

В настоящее время наиболее распространенной позиционной системой счисления являются десятичная система. В информатике широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления.

Десятичная система счисления. В десятичной системе счисления крайняя справа позиция соответствует минимальному значению, в которой цифра обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем тысячи и т.д. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.

Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.

В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:

Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:

Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:

Двоичная система счисления. Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

Например, развернутая запись двоичного числа выглядит следующим образом:

а в свернутой форме:

Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:

Восьмеричная система счисления. В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр (0, 1, 2, 3, 4, 5, 6, 7). Запишем восьмеричное число в свернутой и развернутой форме:

Шестнадцатеричная система счисления. В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр (О, 1, 2,3,4, 5, 6, 7, 8,9, А, В, С, D, Е, F), причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр (10, 11, 12, 13, 14, 15) используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой форме:

Источник

Кодирование и обработка числовой информации

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.

Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.

В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:

XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.

Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.

В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:

Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:

Число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.

Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

Двоичная система счисления. Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

Например, развернутая запись двоичного числа выглядит следующим образом:

Это же число в свернутой форме:

Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т. д.

В информатике широко используются восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр <0, 1, 2, 3, 4, 5, 6, 7>. Запишем восьмеричное число 77 в свернутой и развернутой формах и переведем его в десятичную систему счисления:

77₈ = 7 × 8 1 + 7 × 8 0 = 63₁₀.

В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр <0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F>, причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр <10, 11, 12, 13, 14, 15>используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой формах и переведем его в десятичную систему счисления:

ABCDEF₁₆ = А × 16 5 + В × 16 4 + C × 16 3 + D × 16 2 + Е × 16 1 + F × 16 0 = 10 × 16 5 + 11 × 16 4 + 12 × 16 3 + 13 × 16 2 + 14 × 16 1 + 15 × 16 0 = 11259375₁₀.

1. Чем отличаются позиционные системы счисления от непозиционных?

2. Каково основание десятичной системы счисления? Двоичной системы счисления?

3. Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления?

4. На какую величину в позиционных системах счисления различаются одинаковые цифры, стоящие в соседних разрядах числа?

5. Может ли в качестве цифры использоваться символ буквы?

4.1. Задание с кратким ответом. Запишите числа 3,14₁₀ и 10,1₂ в развернутой форме.

4.2. Задание с кратким ответом. Во сколько раз увеличатся числа 10,1₁₀ и 10,1₂ при переносе запятой на один знак вправо?

4.3. Задание с кратким ответом. При переносе запятой на два знака вправо число 11,11_x увеличилось в 4 раза. Чему равно основание системы счисления x?

4.4. Задание с кратким ответом. Какое минимальное основание может иметь система счисления, если в ней записано число 11? Число 99?

4.5. Задание с кратким ответом. Запишите год, месяц и число своего рождения с помощью римских цифр.

Перевод чисел в позиционных системах счисления

Перевод чисел из двоичной системы счисления в десятичную систему счисления. Преобразование чисел из двоичной системы счисления в десятичную выполнить довольно легко. Для этого необходимо записать двоичное число в развернутой форме и вычислить его значение.

Возьмем любое двоичное число, например 10,11₂. Запишем его в развернутой форме и произведем вычисления:

Перевод целых чисел из десятичной системы счисления в двоичную систему счисления. Алгоритм перевода целого десятичного числа в двоичное следующий:

1) последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы счисления (на 2) до тех пор, пока частное от деления не окажется равным нулю;

2) получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.

В качестве примера рассмотрим перевод десятичного числа 19₁₀ в двоичную систему счисления, записывая результаты в таблицу (табл. 4.2).

Таблица 4.2. Перевод целого числа из десятичной системы счисления в двоичную

В результате получаем двоичное число:

Перевод десятичных дробей в двоичную систему счисления. Алгоритм перевода десятичной дроби в двоичную следующий:

1) последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений;

2) получить искомую двоичную дробь, записав полученные целые части произведений в прямой последовательности.

В качестве примера рассмотрим перевод десятичной дроби 0,75₁₀ в двоичную систему, записывая результаты в таблицу (табл. 4.3).

Таблица 4.3. Перевод дробного числа из десятичной системы счисления в двоичную

В результате получаем двоичную дробь:

4.6. Задание с развернутым ответом. Переведите в десятичную систему двоичные числа: 101₂, 110₂, 111₂

4.7. Задание с развернутым ответом. Переведите целое десятичное число 10₂ в двоичную систему счисления.

4.8. Задание с развернутым ответом. Переведите десятичную дробь 0,25₂ в двоичную систему счисления.

4.9. Задание с развернутым ответом. Переведите десятичное число 10,25₂ в двоичную систему счисления.

Арифметические операции в позиционных системах счисления

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110₂ и 11₂.

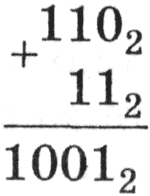Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим.

110₂ = 1 × 2 2 + 1 × 2 1 + 0 × 2 0 = 6₁₀

11₂ = 1 × 2 1 + 1 × 2 0 = 3₁₀

Теперь переведем результат двоичного сложения в десятичное число.

1001₂ = 1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0 = 9₁₀

Сравнение результатов показывает, что сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой.

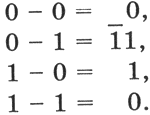Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂.

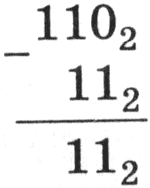Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

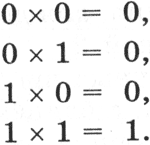Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя. В качестве примера произведем умножение двоичных чисел 110₂ и 11₂.

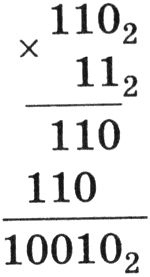Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 110₂ на 11₂.

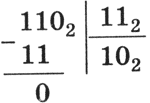Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

4.10. Задание с развернутым ответом. Выполните сложение, вычитание, умножение и деление двоичных чисел 1010₂ и 10₂.

Двоичное кодирование чисел в компьютере

Числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Оперативная память компьютера состоит из ячеек, в каждой из которых может храниться 8 битов информации, т. е. 8 разрядов двоичного числа.

Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т. е. вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А₂ = 11110000₂ будет храниться в ячейке памяти следующим образом:

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целого неотрицательного числа. Минимальное число записывается в восьми разрядах памяти восемью нулями и равно 0. Максимальное число записывается восемью единицами и равно:

Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное, записывается 1).

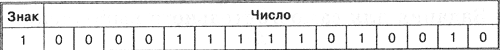Максимальное положительное число (с учетом выделения одного разряда на знак) для данного формата представления равно:

Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые дробные, так и очень большие числа.

Для представления чисел в диапазоне от очень маленьких дробей до очень больших чисел с высокой точностью используется формат с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Число в форме с плавающей запятой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байтов (число двойной точности).

4.11. Задание с развернутым ответом. В каком виде будет храниться в компьютере десятичное число 10₁₀ в формате целого неотрицательного числа и целого числа со знаком?

Источник